Optics Ques 173
- Angular width of central maximum in the Fraunhofer diffraction pattern of a slit is measured. The slit is illuminated by light of wavelength $6000$ $ \AA$. When the slit is illuminated by light of another wavelength, the angular width decreases by $30 \%$. Calculate the wavelength of this light. The same decrease in the angular width of central maximum is obtained when the original apparatus is immersed in a liquid. Find refractive index of the liquid.
$(1996,2 M)$
Show Answer
Answer:
Correct Answer: 173.$4200 $ $\AA, 1.43$
Solution:
Formula:
- (a) Given, $\lambda=6000 \AA$
Let $b$ be the width of slit and $D$ the distance between screen and slit.
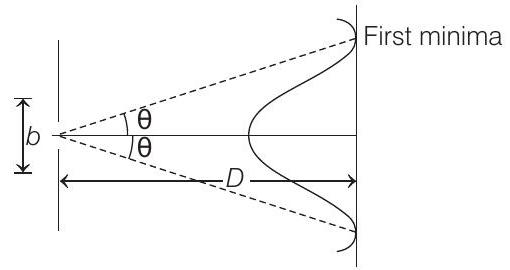
First minima is obtained at $b \sin \theta=\lambda$
or $b \theta=\lambda$ as $\sin \theta \approx \theta$ or $\theta=\frac{\lambda}{b}$
Angular width of first maxima $=2 \theta=\frac{2 \lambda}{b} \propto \lambda$
Angular width will decrease by $30 \%$ when $\lambda$ is also decreased by $30 \%$.
Therefore, new wavelength
$ \begin{aligned} & \lambda^{\prime}=\{(6000)-(\frac{30}{100}) 6000 \}\AA \\ & \lambda^{\prime}=4200 \AA \end{aligned} $
(b) When the apparatus is immersed in a liquid of refractive index $\mu$, the wavelength is decreased $\mu$ times. Therefore,
$ \begin{aligned} 4200 \AA =\frac{6000 \AA}{\mu} \\ \mu =\frac{6000}{4200} \\ \text { or } \mu =1.429 \simeq 1.43 \end{aligned} $





