Optics Ques 175
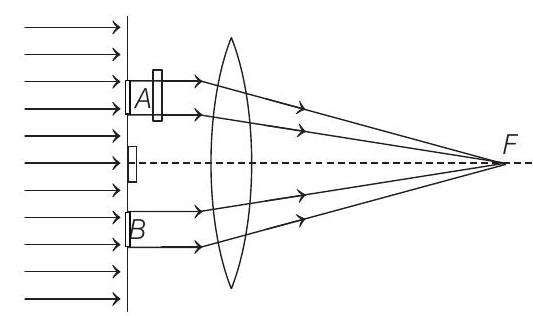
- In a modified Young’s double slit experiment, a monochromatic uniform and parallel beam of light of wavelength $6000 $ $\AA$ and intensity $(10 / \pi)$ $ Wm^{-2}$ is incident normally on two apertures $A$ and $B$ of radii $0.001 $ $m$ and $0.002 $ $m$ respectively. A perfectly transparent film of thickness $2000$ $ \AA$ and refractive index $1.5$ for the wavelength of $6000 $ $\AA$ is placed in front of aperture $A$ (see figure). Calculate the power (in W) received at the focal spot $F$ of the lens. The lens is symmetrically placed with respect to the apertures. Assume that $10 \%$ of the power received by each aperture goes in the original direction and is brought to the focal spot.
$(1989,8 M)$
Show Answer
Answer:
Correct Answer: 175.$(7 \times 10^{-6} W)$
Solution:
Formula:
- Power received by aperture $A$,
$ P _A=I\left(\pi r _A^{2}\right)=\frac{10}{\pi}(\pi)(0.001)^{2}=10^{-5} W $
Power received by aperture $B$,
$ \begin{aligned} P _B=I\left(\pi r _B^{2}\right) & =\frac{10}{\pi}(\pi)(0.002)^{2} \\ & =4 \times 10^{-5} W \end{aligned} $
Only $10 \%$ of $P _A$ and $P _B$ goes to the original direction.
Hence, $\quad 10 \%$ of $P _A=10^{-6}=P _1$ (say)
and $\quad 10 \%$ of $P _B=4 \times 10^{-6}=P _2$ (say)
Path difference created by slab
$ \begin{aligned} \Delta x & =(\mu-1) t \\ & =(1.5-1)(2000)=1000 \AA \end{aligned} $
Corresponding phase difference,
$ \phi=\frac{2 \pi}{\lambda} \cdot \Delta x=\frac{2 \pi}{6000} \times 1000=\frac{\pi}{3} $
Now, resultant power at the focal point
$ \begin{aligned} P & =P _1+P _2+2 \sqrt{P _1 P _2} \cos \phi \\ & =10^{-6}+4 \times 10^{-6}+2 \sqrt{\left(10^{-6}\right)\left(4 \times 10^{-6}\right)} \cos \frac{\pi}{3} \\ & =7 \times 10^{-6} W \end{aligned} $





