Optics Ques 191
- Two thin convex lenses of focal lengths $f _1$ and $f _2$ are separated by a horizontal distance $d$ (where $d<f _1, d<f _2$ ) and their centres are displaced by a vertical separation $\Delta$ as shown in the figure.
(1993)
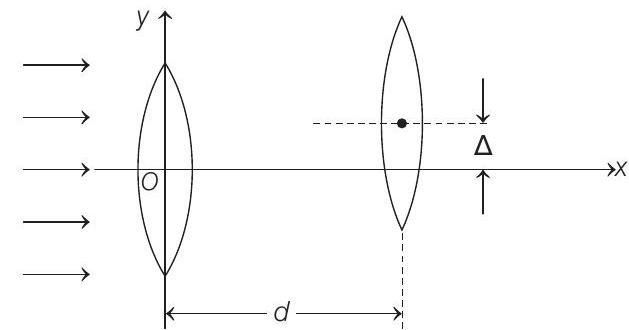
Taking the origin of coordinates, $O$, at the centre of the first lens, the $x$ and $y$-coordinates of the focal point of this lens system, for a parallel beam of rays coming from the left, are given by
(1993; 2M)
(a) $x=\frac{f _1 f _2}{f _1+f _2}, y=\Delta$
(b) $x=\frac{f _1\left(f _2+d\right)}{f _1+f _2-d}, y=\frac{\Delta}{f _1+f _2}$
(c) $x=\frac{f _1 f _2+d\left(f _1-d\right)}{f _1+f _2-d}, y=\frac{\Delta\left(f _1-d\right)}{f _1+f _2-d}$
(d) $x=\frac{f _1 f _2+d\left(f _1-d\right)}{f _1+f _2-d}, y=0$
Show Answer
Answer:
Correct Answer: 191.(c)
Solution:
- From the first lens parallel beam of light is focused at its focus i.e. at a distance $f _1$ from it. This image $I _1$ acts as virtual object for second lens $L _2$. Therefore, for $L _2$
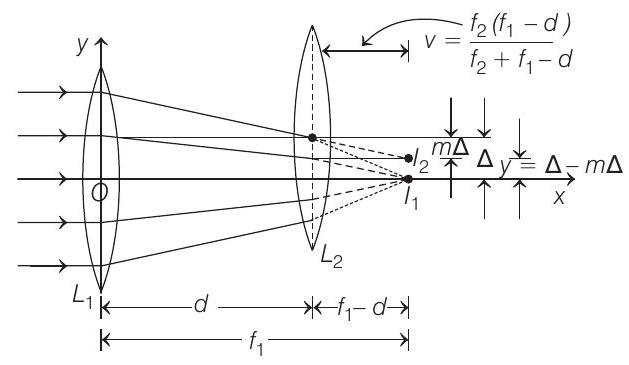
$ u =+\left(f _1-d\right), f=+f _2 $
$ \therefore \frac{1}{v} =\frac{1}{f}+\frac{1}{u}=\frac{1}{f _2}+\frac{1}{f _1-d} $
$\text { Hence, } v =\frac{f _2\left(f _1-d\right)}{f _2+f _1-d}$
Therefore, $x$-coordinate of its focal point will be
$ \begin{aligned} x & =d+v=d+\frac{f _2\left(f _1-d\right)}{f _2+f _1-d} \\ & =\frac{f _1 f _2+d\left(f _1-d\right)}{f _1+f _2-d} \end{aligned} $
Linear magnification for $L _2$
$ \begin{aligned} m & =\frac{v}{u}=\frac{f _2\left(f _1-d\right)}{f _2+f _1-d} \cdot \frac{1}{f _1-d} \\ & =\frac{f _2}{f _2+f _1-d} \end{aligned} $
Therefore, second image will be formed at a distance of $m \Delta$ or $\left(\frac{f _2}{f _2+f _1-d}\right) . \Delta$ below its optic axis.
Therefore, $y$-coordinate of the focus of system will be
$ \text { or } \quad \begin{aligned} & y=\Delta-\left(\frac{f _2 \Delta}{f _2+f _1-d}\right) \\ & y=\frac{\left(f _1-d\right) \cdot \Delta}{f _2+f _1-d} \end{aligned} $





