Optics Ques 211
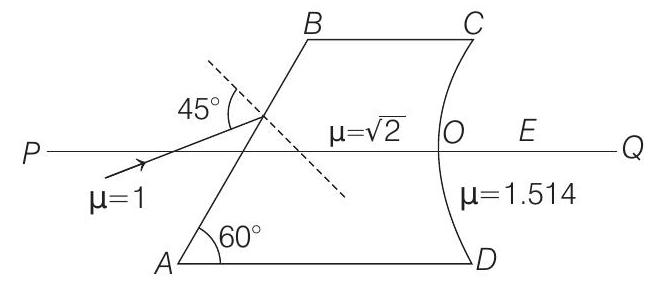
- Figure shows an irregular block of material of refractive index $\sqrt{2}$. A ray of light strikes the face $A B$ as shown in the figure. After refraction it is incident on a spherical surface $C D$ of radius of curvature $0.4 $ $m$ and enters a medium of refractive index $1.514$ to meet $P Q$ at $E$. Find the distance $O E$ upto two places of decimal.
$(2004,2 M)$
Show Answer
Answer:
Correct Answer: 211.$( 6.06$ $ m)$
Solution:
Formula:
Refraction at Spherical Surfaces:
- Applying Snell’s law on face $A B$,
$ (1) \sin 45^{\circ} =(\sqrt{2}) \sin r$
$ \sin r =\frac{1}{2}$
$\text { or } \quad r =30^{\circ}$
i.e. ray becomes parallel to $A D$ inside the block.
Now applying,
$ \begin{gathered} \frac{\mu _2}{v}-\frac{\mu _1}{u}=\frac{\mu _2-\mu _1}{R} \text { on face } C D, \\ \frac{1.514}{O E}-\frac{\sqrt{2}}{\infty}=\frac{1.514-\sqrt{2}}{0.4} \end{gathered} $
Solving this equation, we get $O E=6.06$ $ m$





