Optics Ques 223
- Consider a tank made of glass (refractive index is $1.5$ ) with a thick bottom. It is filled with a liquid of refractive index $\mu$. A student finds that, irrespective of what the incident angle $i$ (see figure) is for a beam of light entering the liquid, the light reflected from the liquid glass interface is never completely polarised. For this to happen, the minimum value of $\mu$ is
(2019 Main, 9 Jan I)
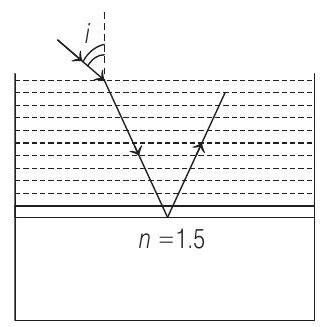
(a) $\frac{3}{\sqrt{5}}$
(b) $\frac{5}{\sqrt{3}}$
(c) $\frac{4}{3}$
(d) $\sqrt{\frac{5}{3}}$
Show Answer
Answer:
Correct Answer: 223.(a)
Solution:
- Key Idea: When a beam of unpolarised light is reflected from a transparent medium of refractive index $\mu$, then the reflected light is completely plane polarised at a certain angle of incidence $i _B$, which is known as Brewster’s angle.
In the given condition, the light reflected irrespective of an angle of incidence is never completely polarised. So,
$ i _C>i _B $
where, $i _C$ is the critical angle.
$ \Rightarrow \quad \sin i _C<\sin i _B $ $\quad$ …….(i)
From Brewster’s law, we know that
$ \tan i _B={ }^{w} \mu _g=\frac{\mu _{\text {glass }}}{\mu _{\text {water }}}=\frac{1.5}{\mu} $ $\quad$ …….(ii)
From Eqs. (i) and (ii), we get
$\frac{1}{\mu}<\frac{1.5}{\sqrt{(1.5)^{2}+(\mu)^{2}}} $
$\Rightarrow \quad \sqrt{(1.5)^{2}+\mu^{2}}<1.5 \mu $
$\mu^{2}+(1.5)^{2}<(1.5 \mu)^{2} \text { or } \mu<\frac{3}{\sqrt{5}} $
$\therefore \text { The minimum value of } \mu \text { should be } \frac{3}{\sqrt{5}} .$





