Optics Ques 28
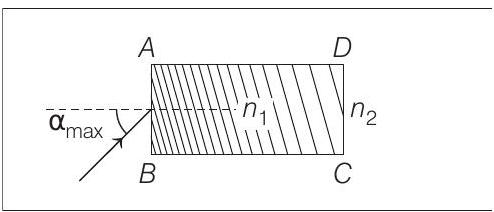
- A rectangular glass slab $A B C D$ of refractive index $n _1$ is immersed in water of refractive index $n _2\left(n _1>n _2\right)$. A ray of light is incident at the surface $A B$ of the slab as shown. The maximum value of the angle of incidence $\alpha _{\max }$, such that the ray comes out only from the other surface $C D$, is given by
$(2000,2 M)$
(a) $\sin ^{-1} [\frac{n _1}{n _2} \cos (\sin ^{-1} \frac{n _2}{n _1})]$
(b) $\sin ^{-1} [n _1 \cos (\sin ^{-1} \frac{1}{n _2})]$
(c) $\sin ^{-1} (\frac{n _1}{n _2})$
(d) $\sin ^{-1} (\frac{n _2}{n _1})$
Show Answer
Answer:
Correct Answer: 28.(a)
Solution:
Formula:
Critical Angle and Total Internal Reflection (T. I. R.)
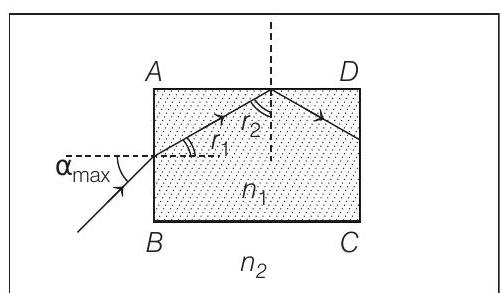
- Rays come out only from $C D$, means rays after refraction from $A B$ get total internally reflected at $A D$. From the figure
$ \begin{gathered} r _1+r _2=90^{\circ} \\ r _1=90^{\circ}-r _2 \\ \quad\left(r _1\right) _{\max }=90^{\circ}-\left(r _2\right) _{\min } \text { and }\left(r _2\right) _{\min }=\theta _C \end{gathered} $
(for total internal reflection at $A D$ )
where,
$ \sin \theta _C=\frac{n _2}{n _1} $
$ \begin{aligned} \text { or } & \theta _C =\sin ^{-1} \frac{n _2}{n _1} \\ \therefore & \quad \left(r _1\right) _{\max } =90^{\circ}-\theta _C \end{aligned} $
Now, applying Snell’s law at face $A B$
$ \begin{aligned} \frac{n _1}{n _2} & =\frac{\sin \alpha _{\max }}{\sin \left(r _1\right) _{\max }} \\ & =\frac{\sin \alpha _{\max }}{\sin \left(90^{\circ}-\theta _C\right)}\\ & =\frac{\sin \alpha _{\max }}{\cos \theta _C} \\ \text { or } \quad \sin \alpha _{\max } & =\frac{n _1}{n _2} \cos \theta _C \\ \therefore \quad \alpha _{\max } & =\sin ^{-1} [\frac{n _1}{n _2} \cos \theta _C] \\ & =\sin ^{-1} [\frac{n _1}{n _2} \cos (\sin ^{-1} \frac{n _2}{n _1})] \end{aligned} $





