Optics Ques 42
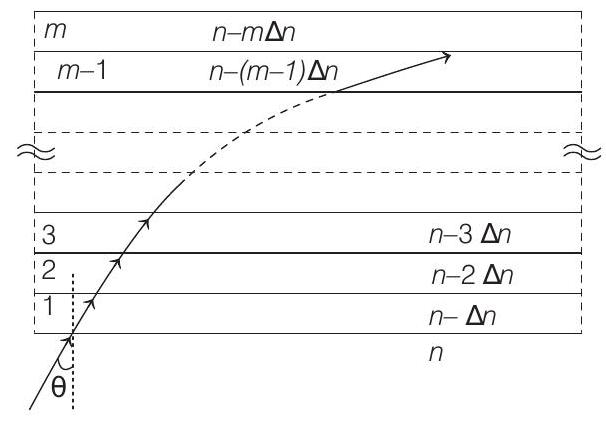
- A monochromatic light is travelling in a medium of refractive index $n=1.6$. It enters a stack of glass layers from the bottom side at an angle $\theta=30^{\circ}$. The interfaces of the glass layers are parallel to each other. The refractive indices of different glass layers are monotonically decreasing as $n _m=n-m \Delta n$, where $n _m$ is the refractive index of the $m$ th slab and $\Delta n=0.1$ (see the figure). The ray is refracted out parallel to the interface between the $(m-1)$ th and $m$ th slabs from the right side of the stack. What is the value of $m$ ?
(2017 Adv.)
Show Answer
Answer:
Correct Answer: 42.8
Solution:
Formula:
Critical Angle and Total Internal Reflection (T. I. R.)
- But this value of refractive index is not possible.
$$ \begin{aligned} 42.6 \sin \theta & =(n-m \Delta n) \sin 90^{\circ} \\ 42.6 \sin \theta & =n-m \Delta n \\ 42.6 \times \frac{1}{2} & =21.3-m(0.1) \\ 42.8 & =1.6-m(0.1) \\ m \times 0.1 & =0.8 \\ m & =8 \end{aligned} $$





