Optics Ques 45
- The $x-y$ plane is the boundary between two transparent media. Medium-1 with $z \geq 0$ has a refractive index $\sqrt{2}$ and medium-2 with $z \leq 0$ has a refractive index $\sqrt{3}$. A ray of light in medium-1 given by vector $\mathbf{A}=6 \sqrt{3} \hat{\mathbf{i}}+8 \sqrt{3} \hat{\mathbf{j}}-10 \hat{\mathbf{k}}$ is incident on the plane of separation. Find the unit vector in the direction of the refracted ray in medium-2.
(1999, 10 M)
Show Answer
Answer:
Correct Answer: 45.$\frac{1}{5 \sqrt{2}}(3 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}-5 \hat{\mathbf{k}})$
Solution:
Formula:
Laws of Refraction (at any Refracting Surface):
- Incident ray $\mathbf{A}=6 \sqrt{3} \hat{\mathbf{i}}+8 \sqrt{3} \hat{\mathbf{j}}-10 \hat{\mathbf{k}}$
$ \begin{aligned} & =(6 \sqrt{3} \hat{\mathbf{i}}+8 \sqrt{3} \hat{\mathbf{j}})+(-10 \hat{\mathbf{k}}) \\ & =\mathbf{Q O}+\mathbf{P Q} \quad \text { (As shown in figure) } \end{aligned} $
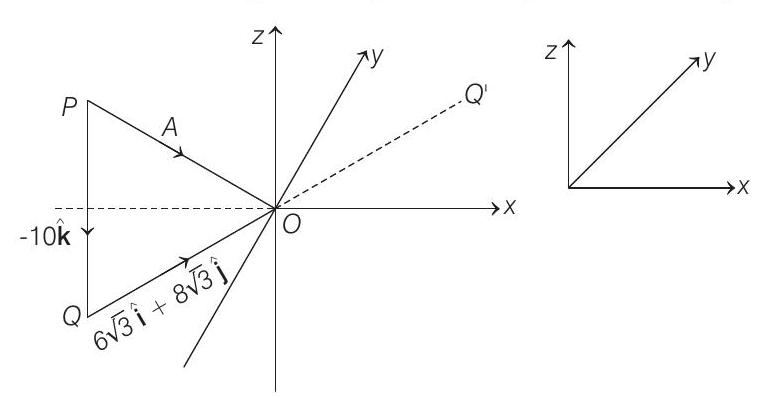
Note that $\mathbf{Q O}$ is lying on $x-y$ plane.
Now, $Q Q^{\prime}$ and $Z$-axis are mutually perpendicular. Hence, we can show them in two-dimensional figure as below.
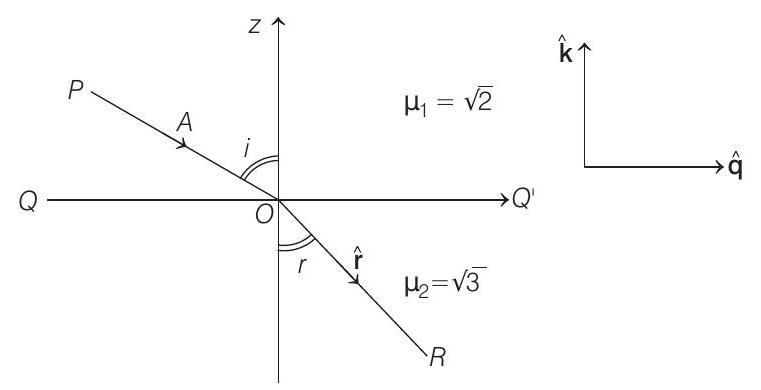
Vector A makes an angle $i$ with $z$-axis, given by
$ \begin{aligned} & i=\cos ^{-1} \{\frac{10}{\sqrt{(10)^{2}+(6 \sqrt{3})^{2}+(8 \sqrt{3})^{2}}}\}=\cos ^{-1} \{\frac{1}{2}\} \\ & i=60^{\circ} \end{aligned} $
Unit vector in the direction of $Q O Q^{\prime}$ will be
$ \begin{gathered} \hat{\mathbf{q}}=\frac{6 \sqrt{3} \hat{\mathbf{i}}+8 \sqrt{3} \hat{\mathbf{j}}}{\sqrt{(6 \sqrt{3})^{2}+(8 \sqrt{3})^{2}}} \\ =\frac{1}{5}(3 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}) \end{gathered} $
Snell’s law gives
$ \begin{array}{rlrl} & & \frac{\sqrt{3}}{\sqrt{2}} & =\frac{\sin i}{\sin r}=\frac{\sin 60^{\circ}}{\sin r} \\ & \therefore & \sin r & =\frac{\sqrt{3} / 2}{\sqrt{3} / \sqrt{2}}=\frac{1}{\sqrt{2}} \\ \therefore & r & =45^{\circ} \end{array} $
Now, we have to find a unit vector in refracted ray’s direction $O R$. Say it is $\hat{\mathbf{r}}$ whose magnitude is 1 . Thus,
$ \begin{aligned} \hat{\mathbf{r}} & =(1 \sin r) \hat{\mathbf{q}}-(1 \cos r) \hat{\mathbf{k}} \\ & =\frac{1}{\sqrt{2}}[\hat{\mathbf{q}}-\hat{\mathbf{k}}]=\frac{1}{\sqrt{2}} [\frac{1}{5}(3 \hat{\mathbf{i}}+4 \hat{\mathbf{j}})-\hat{\mathbf{k}} ]\\ \hat{\mathbf{r}} & =\frac{1}{5 \sqrt{2}}(3 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}-5 \hat{\mathbf{k}}) . \end{aligned} $





