Optics Ques 47
- In figure, the optical fibre is $l=2 $ $m$ long and has a diameter of $d=20$ $ \mu m$. If a ray of light is incident on one end of the fibre at angle $\theta _1=40^{\circ}$, the number of reflections it makes before emerging from the other end is close to (refractive index of fibre is $1.31$ and $\sin 40^{\circ}=0.64$ )
(Main 2019, 8 April I)
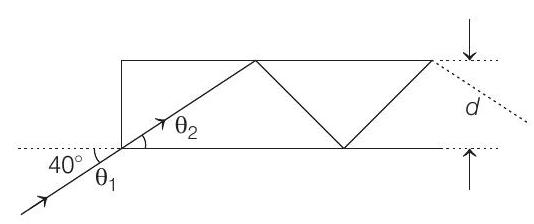
(a) $55000$
(b) $66000$
(c)$ 45000$
(d) $57000$
Show Answer
Answer:
Correct Answer: 47.(d)
Solution:
Formula:
Critical Angle and Total Internal Reflection (T. I. R.)
- Total internal reflection occurs through given glass rod as shown in figure.
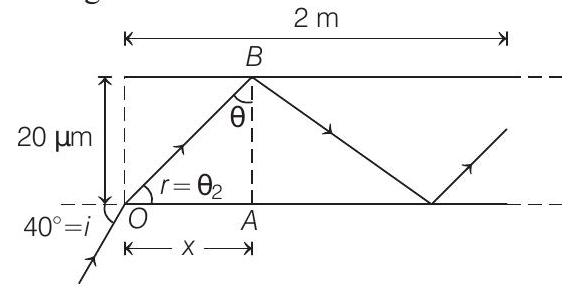
From Snell’s law, $n _1 \sin i=n _2 \sin r$
where, $n _1=1, n _2=1.31$ and $i=40^{\circ}$
So, we get
$1 \sin 40^{\circ}=1.31 \sin r \Rightarrow \sin r=\frac{0.64}{1.31}=0.49 \approx 0.5$
So, $r=30^{\circ}$
From $\triangle O A B, \theta=90-r=60^{\circ}$
Now, $\tan \theta=\frac{x}{20 \mu m}$
$ \Rightarrow \quad x=20 \sqrt{3} \mu m \quad\left[\because \tan 60^{\circ}=\sqrt{3}\right] $
One reflection occurs in $20 \sqrt{3} \mu m$.
$\therefore$ Total number of reflections occurring in $2 m$
$ \begin{aligned} & =n=\frac{2 m}{20 \sqrt{3} \mu m}=\frac{2}{20 \sqrt{3} \times 10^{-6}} \\ & =57735 \text { reflections } \approx 57000 \text { reflections } \end{aligned} $





