Optics Ques 61
- A bi-convex lens is formed with two thin plano-convex lenses as shown in the figure. Refractive index $n$ of the first lens is $1.5$ and that of the second lens is $1.2$. Both the curved surfaces are of the same radius of curvature $R=14$ $ cm$. For this bi-convex lens, for an object distance of $40 $ $cm$, the image distance will be
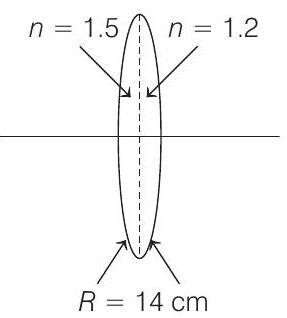
(2012)
(a) $-280.0$ $ cm$
(b) $40.0$ $ cm$
(c) $21.5$ $ cm$
(d) $13.3$ $ cm$
Show Answer
Answer:
Correct Answer: 61.(b)
Solution:
Formula:
- Using the lens formula,
$ \begin{alignedat} \frac{1}{v}-\frac{1}{u} & =\frac{1}{F}=\frac{1}{f _1}+\frac{1}{f _2} \text { or } \frac{1}{v}=\frac{1}{u}+\frac{1}{f _1}+\frac{1}{f _2} \\ & =\frac{1}{u}+\left(n _1-1\right) \left(\frac{1}{R _1}-\frac{1}{R _2}\right)+\left(n _2-1\right) \left(\frac{1}{R _1^{\prime}}-\frac{1}{R _2^{\prime}}\right) \end{aligned} $
Substituting the values, we get
$ \frac{1}{v}=\frac{1}{-40}+(1.5-1) (\frac{1}{14}-\frac{1}{\infty})+(1.2-1)( \frac{1}{\infty}-\frac{1}{-14}) $
Solving these equations, we get
$ v=+40 cm $





