Optics Ques 85
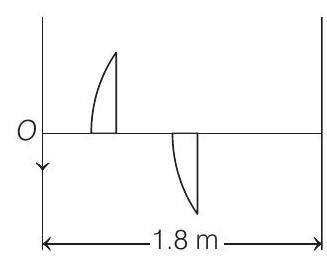
- A thin plano-convex lens of focal length $f$ is split into two halves. One of the halves is shifted along the optical axis. The separation between object and image planes is $1.8$ $ m$. The magnification of the image formed by one of the half lens is $2$. Find the focal length of the lens and separation between the halves. Draw the ray diagram for image formation.
$(1996,5$ M)
Show Answer
Answer:
Correct Answer: 85.$0.4 $ $ m, 0.6 $ $m$
Solution:
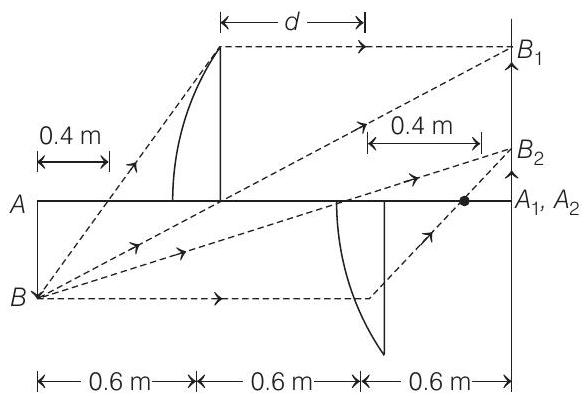
- For both the halves, position of object and image is same. Only difference is of magnification. Magnification for one of the halves is given as $2(>1)$. This can be for the first one, because for this, $|v|>|u|$. Therefore, magnification, $|m|=|v / u|>1$. So, for the first half
$ |v / u|=2 \text { or } \quad|v|=2|u| $
Let $u=-x$ then $v=+2 x$ and $|u|+|v|=1.8 $ $m$
i.e. $\quad 3 x=1.8$ $ m$ or $x=0.6$ $ m$
Hence, $u=-0.6 $ $ m$ and $v=+1.2 $ $m$.
Using, $\frac{1}{f}=\frac{1}{v}-\frac{1}{u}=\frac{1}{1.2}-\frac{1}{-0.6}=\frac{1}{0.4}$
$ \therefore \quad f=0.4 $ $m $
For the second half
$ \begin{aligned} \frac{1}{f} & =\frac{1}{1.2-d}-\frac{1}{-(0.6+d)} \\ \frac{1}{0.4} & =\frac{1}{1.2-d}+\frac{1}{0.6+d} \end{aligned} $
Solving this, we get $d=0.6$ $ m$.
Magnification for the second half will be
$ m _2=\frac{v}{u}=\frac{0.6}{-(1.2)}=-\frac{1}{2} $
and magnification for the first half is
$ m _1=\frac{v}{u}=\frac{1.2}{-(0.6)}=-2 $
The ray diagram is as follows :