Optics Ques 87
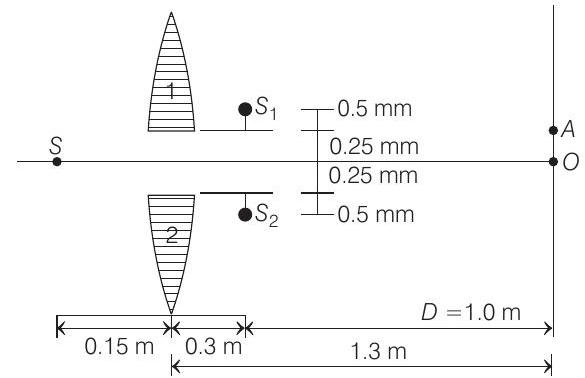
- In given figure, $S$ is a monochromatic point source emitting light of wavelength $\lambda=500$ $ nm$. A thin lens of circular shape and focal length $0.10 $ $m$ is cut into two identical halves $L _1$ and $L _2$ by a plane passing through a diameter. The two halves are placed symmetrically about the central axis $S O$ with a gap of $0.5$ $ mm$. The distance along the axis from $S$ to $L _1$ and $L _2$ is $0.15 $ $m$ while that from $L _1$ and $L _2$ to $O$ is $1.30$ $ m$. The screen at $O$ is normal to $S O$.
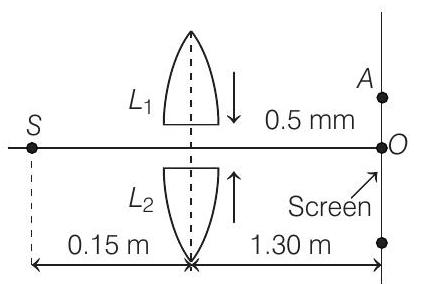
$(1993,5+1 M)$
(a) If the third intensity maximum occurs at the point $A$ on the screen, find the distance $O A$.
(b) If the gap between $L _1$ and $L _2$ is reduced from its original value of $0.5$ $ mm$, will the distance $O A$ increase, decrease, or remain the same.
Show Answer
Answer:
Correct Answer: 87.(a) $1$ $mm$ (b) Increase
Solution:
- (a) For the lens, $u=-0.15 $ $m ; f=+0.10 $ $m$
Therefore, using $\frac{1}{v}-\frac{1}{u}=\frac{1}{f}$ we have
$\frac{1}{v}=\frac{1}{u}+\frac{1}{f}=\frac{1}{(-0.15)}+\frac{1}{(0.10)}$ or $v=0.3$ $ m$
Linear magnification, $m=\frac{v}{u}=\frac{0.3}{-0.15}=-2$
Hence, two images $S _1$ and $S _2$ of $S$ will be formed at $0.3$ $ m$ from the lens as shown in figure. Image $S _1$ due to part 1 will be formed at $0.5 $ $mm$ above its optic axis $(m=-2)$.
Similarly, $S _2$ due to part $2$ is formed $0.5$ $ mm$ below the optic axis of this part as shown.
Hence, $d=$ distance between $S _1$ and $S _2=1.5$ $ mm$
$ \begin{aligned} D & =1.30-0.30=1.0 m=10^{3} mm \\ \lambda & =500 nm=5 \times 10^{-4} mm \end{aligned} $
Therefore, fringe width,
$ \omega=\frac{\lambda D}{d}=\frac{\left(5 \times 10^{-4}\right)\left(10^{3}\right)}{(1.5)}=\frac{1}{3}$ $ mm $
Now, as the point $A$ is at the third maxima
$ O A=3 \omega=3(1 / 3)$ $ mm \quad \text { or } O A=1$ $ mm $
NOTE: The language of the question is slightly confusing. The third intensity maximum may be understood as second order maximum (zero order, first order and the second order). In that case $O A=2 \omega=2(1 / 3)$ $ mm=0.67 $ $mm$.
(b) If the gap between $L _1$ and $L _2$ is reduced, $d$ will decrease. Hence, the fringe width $\omega$ will increase or the distance $O A$ will increase.