Optics Ques 88
- A plano-convex lens has a thickness of $4 $ $cm$. When placed on a horizontal table, with the curved surface in contact with it, the apparent depth of the bottom most point of the lens is found to be $3 $ $cm$. If the lens is inverted such that the plane face is in contact with the table, the apparent depth of the centre of the plane face is found to be $25 / 8 $ $cm$. Find the focal length of the lens. Assume thickness to be negligible while finding its focal length.
(1984, 6M)
Show Answer
Answer:
Correct Answer: 88.$75$ $cm$
Solution:
Formula:
Refraction at Spherical Thin Lens:
- Refer figure (a)
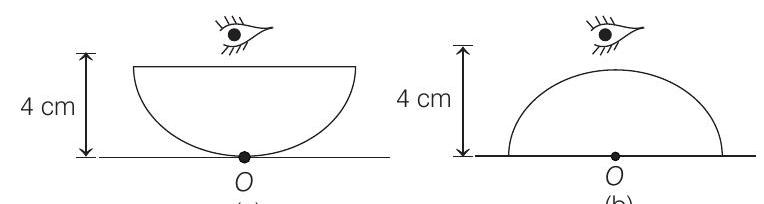
In this case refraction of the rays starting from $O$ takes place from a plane surface. So, we can use
$ d _{\text {app }}=\frac{d _{\text {actual }}}{\mu} \quad \text { or } \quad 3=\frac{4}{\mu} \quad \text { or } \quad \mu=\frac{4}{3} $
Refer figure (b)
In this case refraction takes place from a spherical surface. Hence, applying
$\frac{\mu _2}{v}-\frac{\mu _1}{u}=\frac{\mu _2-\mu _1}{R} $
$\text { we have, } \frac{1}{(-25 / 8)}-\frac{4 / 3}{-4}=\frac{1-4 / 3}{-R} $
$\text { or } \quad \frac{1}{3 R} =\frac{1}{3}-\frac{8}{25}=\frac{1}{75} $
$\therefore \quad R =25 $ $cm$
Now, to find the focal length we will use the lens Maker’s formula
$ \begin{aligned} \frac{1}{f} & =(\mu-1) (\frac{1}{R _1}-\frac{1}{R _2})=(\frac{4}{3}-1) (\frac{1}{\infty}-\frac{1}{-25})=\frac{1}{75} \\ \therefore \quad f & =75 cm \end{aligned} $





