Optics Ques 98
- A monochromatic light is incident at a certain angle on an equilateral triangular prism and suffers minimum deviation. If the refractive index of the material of the prism is $\sqrt{3}$, then the angle of incidence is
(2019 Main, 11 Jan II)
(a) $45^{\circ}$
(b) $90^{\circ}$
(c) $60^{\circ}$
(d) $30^{\circ}$
Show Answer
Answer:
Correct Answer: 98.(c)
Solution:
Formula:
- Given, refractive index of material of prism $n=\sqrt{3}$, prism angle $A=60^{\circ}$
Method 1
Using prism formula,
$ n =\frac{\sin (\frac{A+\delta}{2})}{\sin (\frac{A}{2})} $
$\Rightarrow \quad \sin (\frac{60+\delta}{2} )=\frac{\sqrt{3}}{2} $
$\Rightarrow \quad \sin (\frac{60+\delta}{2}) =\sin 60^{\circ} $
$\Rightarrow \quad (\frac{60+\delta}{2}) =60$
or angle of minimum deviation $\delta=60^{\circ}$
Incident angle, $\quad i=\frac{60+\delta}{2}=60^{\circ}$
Method 2
For minimum deviation, ray should pass symmetrically (i.e. parallel to the base of the equilateral prism)
$\Rightarrow$ From geometry of given figure, we have, $r=30^{\circ}$
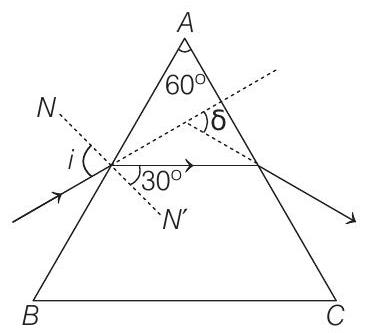
Using Snell’s law,
$ \begin{aligned} n & =\frac{\sin i}{\sin r} \\ \sin i & =n \sin r=\sqrt{3} \sin 30^{\circ} \\ \Rightarrow \quad \sin i & =\frac{\sqrt{3}}{2} \text { or } i=60^{\circ} \end{aligned} $





