Simple Harmonic Motion Ques 31
- A uniform cylinder of length $L$ and mass $M$ having cross-sectional area $A$ is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half-submerged in a liquid of density $\rho$ at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with a small amplitude. If the force constant of the spring is $k$, the frequency of oscillation of the cylinder is
$(1990,2 M)$
(a) $\frac{1}{2 \pi} (\frac{k-A \rho g}{M})^{1 / 2}$
(b) $\frac{1}{2 \pi} (\frac{k+A \rho g}{M})^{1 / 2}$
(c) $\frac{1}{2 \pi} (\frac{k+\rho g L^{2}}{M})^{1 / 2}$
(d) $\frac{1}{2 \pi} (\frac{k+A \rho g}{A \rho g})^{1 / 2}$
Show Answer
Answer:
Correct Answer: 31.(b)
Solution:
Formula:
- When cylinder is displaced by an amount $x$ from its mean position, spring force and upthrust both will increase. Hence,
Net restoring force $=$ extra spring force + extra upthrust
or $ \quad F=-(k x+A x \rho g) $
or $\quad a=-\frac{k+\rho A g}{M} x$
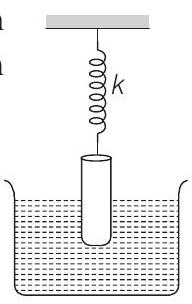
Now, $\quad f=\frac{1}{2 \pi} \sqrt{\left|\frac{a}{x}\right|}=\frac{1}{2 \pi} \sqrt{\frac{k+\rho A g}{M}}$
$\therefore$ Correct option is (b).





