Simple Harmonic Motion Ques 47
- A uniform rod of length $L$ and mass $M$ is pivoted at the centre. Its two ends are attached to two springs of equal spring constants $k$. The springs are fixed to rigid supports as shown in the figure, and rod is free to oscillate in the horizontal plane.
The rod is gently pushed through a small angle $\theta$ in one direction and released. The frequency of oscillation is (2009)
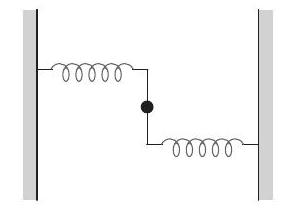
(a) $\frac{1}{2 \pi} \sqrt{\frac{2 k}{M}}$
(b) $\frac{1}{2 \pi} \sqrt{\frac{k}{M}}$
(c) $\frac{1}{2 \pi} \sqrt{\frac{6 k}{M}}$
(d) $\frac{1}{2 \pi} \sqrt{\frac{24 k}{M}}$
Show Answer
Answer:
Correct Answer: 47.(c)
Solution:
Formula:
- $x=\frac{L}{2} \theta$,
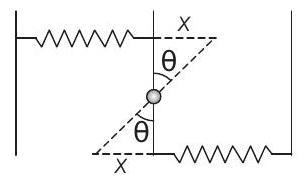
Restoring torque $=-(2 k x) \cdot \frac{L}{2}$
$ \begin{aligned} \alpha & =-\frac{k L(L / 2 \theta)}{I}=-[\frac{k L^{2} / 2}{M L^{2} / 12} ]\cdot \theta=-\frac{6 k}{M} \theta \\ \therefore \quad f & =\frac{1}{2 \pi} \sqrt{\left|\frac{\alpha}{\theta}\right|}=\frac{1}{2 \pi} \sqrt{\frac{6 k}{M}} \end{aligned} $





