Simple Harmonic Motion Ques 62
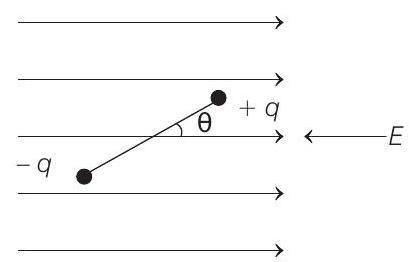
- A point particle of mass $M$ attached to one end of a massless rigid non- conducting rod of length $L$. Another point particle of the same mass is attached to the other end of the rod. The two particles carry charges $+q$ and $-q$ respectively. This arrangement is held in a region of a uniform electric field $E$ such that the rod makes a small angle $\theta$ (say of about 5 degrees) with the field direction. Find an expression for the minimum time needed for the rod to become parallel to the field after it is set free. $(1989,8 M)$
Show Answer
Answer:
Correct Answer: 62.$\frac{\pi}{2} \sqrt{\frac{M L}{2 q E}}$
Solution:
Formula:
Electric Dipole in Uniform Electric Field :
- A torque will act on the rod, which tries to align the rod in the direction of electric field. This torque will be of restoring nature and has a magnitude $P E \sin \theta$. Therefore, we can write
$ \tau=-P E \sin \theta \quad \text { or } \quad I \alpha=-P E \sin \theta $ $\quad$ …….(i)
Here, $\quad I=2 M \quad \frac{L^{2}}{2}=\frac{M L^{2}}{2}$ and $P=q L$
Further, since $\theta$ is small so, we can write, $\sin \theta \approx \theta$.
Substituting these values in Eq. (i), we have
$ (\frac{M L^{2}}{2}) \alpha=-(q L)(E) \theta $
or
$ \alpha=-(\frac{2 q E}{M L}) \theta $
As $\alpha$ is proportional to $-\theta$, motion of the rod is simple harmonic in nature, time period of which is given by
$ T=2 \pi \sqrt{\left|\frac{\theta}{\alpha}\right|}=2 \pi \sqrt{\frac{M L}{2 q E}} $
The desired time will be,
$ t=\frac{T}{4}=\frac{\pi}{2} \sqrt{\frac{M L}{2 q E}} $





