Simple Harmonic Motion Ques 64
- A cylindrical plastic bottle of negligible mass is filled with $310$ $mL$ of water and left floating in a pond with still water. If pressed downward slightly and released, it starts performing simple harmonic motion at angular frequency $\omega$. If the radius of the bottle is $2.5$ $cm$, then $\omega$ is close to (Take, density of water $=10^{3} kg / m^{3}$ )
(a) $2.50$ $ rad$ $s^{-1}$
(b) $5.00$ $ rad$ $s^{-1}$
(c) $1.25$ $ rad$ $s^{-1}$
(d) $3.75$ $ rad$ $s^{-1}$
(2019 Main, 10 Jan II)
Show Answer
Answer:
Correct Answer: 64.$(*)$
Solution:
Formula:
- In equilibrium condition bottle floats in water and its length ’ $l$ ’ inside water is same as the height of water upto which bottle is filled.
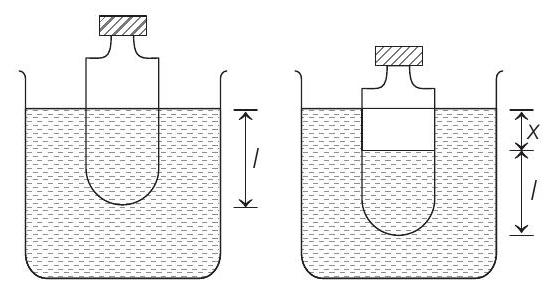
So, $l=$ Volume of water in bottle/Area
$ =\frac{310}{\pi \times(2.5)^{2}}=15.8 cm=0.158 m $
When bottle is slightly pushed inside by an amount $x$ then, restoring force acting on the bottle is the upthrust of fluid displaced when bottle goes into liquid by amount $x$.
So, restoring force is;
$ F=-(\rho A x) g $ $\quad$ …….(i)
where $\rho=$ density of water,
$A=$ area of cross-section of bottle and
$x=$ displacement from equilibriumposition
But $F=m a$ $\quad$ …….(ii)
where, $\quad m=$ mass of water and bottle system
$ =A l \rho $
From (i) and (ii) we have,
$ A l \rho \alpha=-\rho A x g \text { or } a=-\frac{g}{l} x $
As for SHM, $a=-\omega^{2} x$
We have $\omega=\sqrt{\frac{g}{l}}=\sqrt{\frac{10}{0.158}}=\sqrt{63.29} \approx 8$ $rad$ $s^{-1}$
$\therefore$ No option is correct.





