Solution

(i) ${ }^{2-\sqrt{5}}=2-2.2360679 \ldots$

$=-0.2360679 \ldots$

As the decimal expansion of this expression is non-terminating non-recurring, therefore, it is an irrational number.

(ii)

$ (3+\sqrt{23})-\sqrt{23}=3=\frac{3}{1} \quad \text{ number. form, therefore, it is a } $

As it can be represented in $\frac{p}{q}$

(iii) $\frac{2 \sqrt{7}}{7 \sqrt{7}}=\frac{2}{7}$ : $\frac{2 \sqrt{7}}{7 \sqrt{7}}=\frac{2}{7}$, which is a rational number.

(iv) $\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}=0.7071067811 \ldots$

As the decimal expansion of this expression is non-terminating non-recurring, therefore, it is an irrational number. ( $v)$

$2 п=2(3.1415 \ldots)$

$=6.2830 \ldots$

As the decimal expansion of this expression is non-terminating non-recurring, therefore, it is an irrational number.

Solution

$ \begin{aligned} & (3+\sqrt{3})(2+\sqrt{2})=3(2+\sqrt{2})+\sqrt{3}(2+\sqrt{2}) \\ & =6+3 \sqrt{2}+2 \sqrt{3}+\sqrt{6} \\ & \quad(3+\sqrt{3})(3-\sqrt{3})=(3)^{2}-(\sqrt{3})^{2} \\ & \text{ (ii) } \\ & =9-3=6 \\ & \text{ (iii) }(\sqrt{5}+\sqrt{2})^{2}=(\sqrt{5})^{2}+(\sqrt{2})^{2}+2(\sqrt{5})(\sqrt{2}) \\ & =5+2+2 \sqrt{10}=7+2 \sqrt{10} \\ & \text{ (iv) }(\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})=(\sqrt{5})^{2}-(\sqrt{2})^{2} \\ & =5-2=3 \end{aligned} $

Solution

There is no contradiction. When we measure a length with scale or any other instrument, we only obtain an approximate rational value. We never obtain an exact value. For this reason, we may not realise that either $c$ or $d$ is irrational. Therefore,

the $\quad \frac{c}{d}$ fraction is irrational. Hence, $\pi$ is irrational.

Solution

Mark a line segment $O B=9.3$ on number line. Further, take $B C$ of 1 unit. Find the midpoint D of OC and draw a semi-circle on OC while taking D as its centre. Draw a

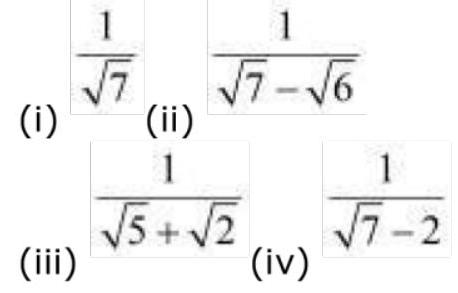
(i)

$\frac{1}{\sqrt{7}}=\frac{1 \times \sqrt{7}}{1 \times \sqrt{7}}=\frac{\sqrt{7}}{7}$

perpendicular to line $O C$ passing through point $B$. Let it intersect the semi-circle at $E$.

Taking B as centre and BE as radius, draw an arc in tersecting number line at $F$. BF is $\sqrt{9.3}$.

Solution

(i)

$ \begin{aligned} 64^{\frac{1}{2}} & =(2^{6})^{\frac{1}{2}} & =2^{2}=4 \\ & =2^{6 \times \frac{1}{2}} & {[(a^{m})^{n}=a^{m m !}] _{(16)^{\frac{3}{4}}=(2^{4})^{\frac{3}{4}}}^{(iii)} } \\ & =2^{3}=8 & \end{aligned} $

$ =2^{5 \times \frac{2}{3}} \quad[(a^{m})^{n \prime}=a^{m m n}] $

(ii)

$ \begin{aligned} 32^{\frac{1}{5}} & =(2^{5})^{\frac{1}{5}} \\ & =(2)^{5 \times \frac{1}{5}} \\ & =2^{1}=2 \end{aligned} $

$ \begin{aligned} & =2^{4 \times \frac{3}{4}} \\ & {[(a^{m})^{n}=a^{m m}]} \\ & {[(a^{m})^{n}=a^{m m}] _{(125)^{\frac{-1}{3}}}^{(iv)}=\frac{1}{(125)^{\frac{1}{3}}}} \\ & =2^{3}=8 \end{aligned} $

$(125)^{\frac{1}{3}}=(5^{3})^{\frac{1}{3}}$

$ \begin{matrix} =5^{3 \times \frac{1}{3}} & {[(a^{m})^{n}=a^{m m}]} & =\frac{1}{5^{3 \times \frac{1}{3}}} \\ =5^{1}=5 & =\frac{1}{5} \end{matrix} $

$ [a^{-m}=\frac{1}{a^{m}}] $