Chapter 07 Triangles Exercise-03
EXERCISE 7.3
1. $\triangle \mathrm{ABC}$ and $\triangle \mathrm{DBC}$ are two isosceles triangles on the same base $\mathrm{BC}$ and vertices $\mathrm{A}$ and $\mathrm{D}$ are on the same side of $\mathrm{BC}$ (see Fig. 7.39). If $\mathrm{AD}$ is extended to intersect $\mathrm{BC}$ at $\mathrm{P}$, show that
(i) $\triangle \mathrm{ABD} \cong \triangle \mathrm{ACD}$
(ii) $\triangle \mathrm{ABP} \cong \triangle \mathrm{ACP}$
(iii) AP bisects $\angle \mathrm{A}$ as well as $\angle \mathrm{D}$.
(iv) $\mathrm{AP}$ is the perpendicular bisector of $\mathrm{BC}$.
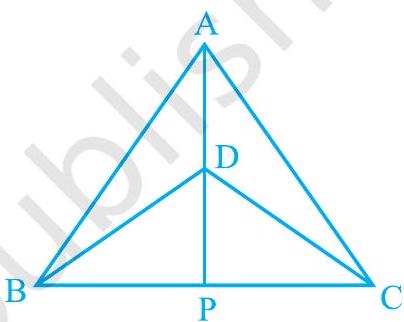
Fig. 7.39
Show Answer
Solution
(i) In $\triangle A B D$ and $\triangle A C D$,
$ \begin{aligned} & A B=A C \ldots \text {…(since } \triangle A B C \text { is isosceles) } \\ & A D=A D \ldots \text {…(common side) } \\ & B D=D C \text {…(since } \triangle \mathrm{BDC} \text { is isosceles) } \\ & \triangle \mathrm{ABD} \cong \triangle \mathrm{ACD} \text {…..SSS test of congruence, } \\ & \therefore \angle \mathrm{BAD}=\angle \mathrm{CAD} \text { i.e. } \angle \mathrm{BAP}=\angle \mathrm{PAC} \text {…..[c.a.c.t]…..(i) } \end{aligned} $
(ii) In $\triangle A B P$ and $\triangle A C P$,
$ \begin{aligned} & A B=A C \ldots \text {…(since } \triangle A B C \text { is isosceles) } \\ & A P=A P \ldots \text {…ommon side) } \\ & \angle B A P=\angle P A C \text {….from (i) } \\ & \triangle A B P \cong \triangle A C P \text {…. SAS test of congruence } \\ & \therefore B P=P C \text {…[C.s.c.t]…..(ii) } \\ & \angle A P B=\angle A P C \text {….c.a.c.t. } \end{aligned} $
(iii) Since $\triangle A B D \cong \triangle A C D$
$ \angle \mathrm{BAD}=\angle \mathrm{CAD} \text {….from (i) } $
So, $A$ bisects $\angle A$
i.e. AP bisects $\angle A$…..(iii)
In $\triangle \mathrm{BDP}$ and $\triangle \mathrm{CDP}$,
DP $=$ DP …common side
$B P=P C$…from (ii)
$\mathrm{BD}=\mathrm{CD}$…(since $\triangle \mathrm{BDC}$ is isosceles)
$\triangle \mathrm{BDP} \cong \triangle \mathrm{CDP}$….SSS test of congruence
$\therefore \angle \mathrm{BDP}=\angle \mathrm{CDP}$….c.a.c.t.
$\therefore \mathrm{DP}$ bisects $\angle \mathrm{D}$
So, AP bisects $\angle \mathrm{D}$
From (iii) and (iv),
AP bisects $\angle \mathrm{A}$ as well as $\angle \mathrm{D}$.
(iv) We know that
$\angle A P B+\angle A P C=180^{\circ} \ldots$ (angles in linear pair)
Also, $\angle \mathrm{APB}=\angle \mathrm{APC}$… from (ii)
$\therefore \angle \mathrm{APB}=\angle \mathrm{APC}=\frac{180^{\circ}}{2}=90^{\circ}$
$\mathrm{BP}=\mathrm{PC}$ and $\angle \mathrm{APB}=\angle \mathrm{APC}=90^{\circ}$
Hence, $\mathrm{AP}$ is perpendicular bisector of $\mathrm{BC}$.
2. $A D$ is an altitude of an isosceles triangle $A B C$ in which $A B=A C$. Show that
(i) $\mathrm{AD}$ bisects $\mathrm{BC}$
(ii) $\mathrm{AD}$ bisects $\angle \mathrm{A}$.
Show Answer
Solution
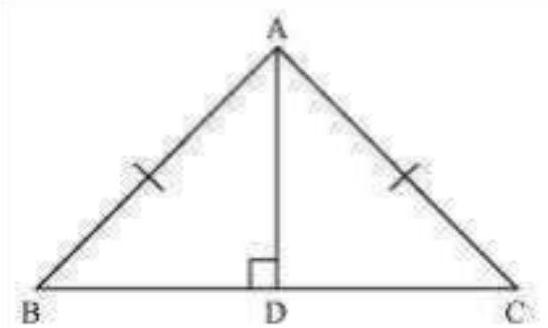
(i) In $\triangle B A D$ and $\triangle C A D$,
$\therefore A D B=\therefore A D C$ (Each $90^{\circ}$ as AD is an altitude)
$A B=A C$ (Given)
$A D=A D$ (Common)
$\therefore \quad \triangle BAD \therefore \triangle CAD$ (By RHS Congruence rule)
$\therefore \quad BD=CD(By CPCT)$
Hence, $A D$ bisects $B C$.
(ii) Also, by CPCT,
$\therefore B A D=C A D$ Hence, $A D$
bisects A. :
3. Two sides $\mathrm{AB}$ and $\mathrm{BC}$ and median $\mathrm{AM}$ of one triangle $\mathrm{ABC}$ are respectively equal to sides $\mathrm{PQ}$ and $\mathrm{QR}$ and median $P N$ of $\triangle P Q R$ (see Fig. 7.40). Show that:
(i) $\triangle \mathrm{ABM} \cong \triangle \mathrm{PQN}$
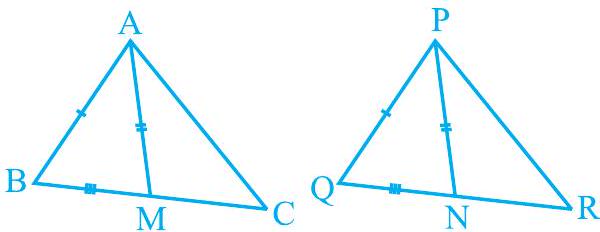
(ii) $\triangle \mathrm{ABC} \cong \triangle \mathrm{PQR}$
Fig. 7.40
Show Answer
Solution
(i) In $\triangle A B C, A M$ is the median to $B C$.
$ \begin{aligned} & \therefore \quad BM={ }^{\frac{1}{2}} BC \\ & \therefore \quad Q N={ }^{\frac{1}{2}} QR \end{aligned} $
However, $BC=QR$
$\therefore{ }^{\frac{1}{2}} _{BC}{ }^{\frac{1}{2}} QR$
$\therefore \quad BM=QN \ldots$ (1)
In $\triangle A B M$ and $\triangle P Q N$, In $\triangle P Q R, P N$ is the median to $Q R$.
$ \begin{aligned} & A B=P Q \text{ (Given) } \\ & BM=QN[\text{ From equation (1)] } \\ & A M=P N(\text{ Given) } \\ & \therefore \quad \therefore \quad \triangle ABM \quad \triangle PQN \text{ (SSS congruence rule) } \\ & \therefore \quad \therefore \quad A B M=P Q N(B y C P C T) \\ & \therefore \quad \therefore \quad A B C=P Q R \ldots(2) \end{aligned} $
(ii) In $\triangle A B C$ and $\triangle P Q R$,
$A B=P Q$ (Given)
$\therefore A B C=\therefore P Q R$ [From equation (2)]
$BC=QR$ (Given)
$\therefore \triangle ABC \therefore \triangle PQR$ (By SAS congruence rule)
4. $\mathrm{BE}$ and $\mathrm{CF}$ are two equal altitudes of a triangle $\mathrm{ABC}$. Using RHS congruence rule, prove that the triangle $\mathrm{ABC}$ is isosceles.
Show Answer
Solution
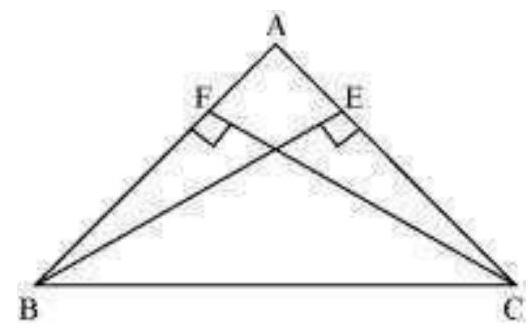
In $\triangle B E C$ and $\triangle C F B$,
$\therefore BEC=\therefore CFB(.$ Each $.90^{\circ})$
$BC=CB$ (Common)
$B E=C F$ (Given)
$\therefore \triangle BEC \quad \triangle CFB$ (By RHS congruency)
$\therefore B B^{\prime} C=C B ‘(B y C P C T)$
$\therefore A B=A C$ (Sides opposite to equal angles of a triangle are equal)
Hence, $\triangle ABC$ is isosceles.
5. $\mathrm{ABC}$ is an isosceles triangle with $\mathrm{AB}=\mathrm{AC}$. Draw $\mathrm{AP} \perp \mathrm{BC}$ to show that $\angle \mathrm{B}=\angle \mathrm{C}$.
Show Answer
Solution
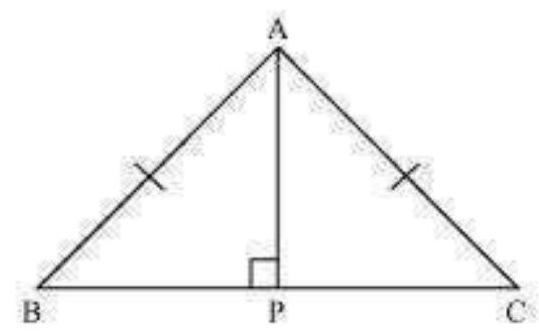
In $\triangle A P B$ and $\triangle A P C$,
$\therefore APB=\therefore APC(.$ Each $.90^{\circ})$
$A B=A C($ Given $)$
$A P=A P($ Common $)$
$\therefore \triangle APB \quad \triangle APC$ (Using RHS congruence rule)
$\therefore B^{\prime \prime}=C$ (By using CPCT)





