Chapter 08 Quadrilaterals Exercise-01
EXERCISE 8.1
1. If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Show Answer
Solution
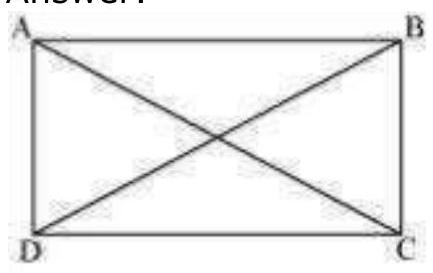
Let $A B C D$ be a parallelogram. To show that $A B C D$ is a rectangle, we have to prove that one of its interior angles is $90^{\circ}$.
In $\triangle A B C$ and $\triangle D C B$,
$A B=D C$ (Opposite sides of a parallelogram are equal)
$BC=BC($ Common)
$AC=DB$ (Given)
$\therefore \triangle ABC \triangle DCB$ (By SSS Congruence rule)
$\Rightarrow$
$A B C=D C B$
It is known that the sum of the measures of angles on the same side of transversal is $180^{\circ}$.
$ \begin{matrix} \angle \angle & ABC+DCB=180^{\circ}(AB|| CD) \\ \Rightarrow \angle & ABC+\angle ABC=180^{\circ} \\ \Rightarrow 2 \angle & ABC=180^{\circ} \\ \Rightarrow \angle & ABC=90^{\circ} \end{matrix} $
Since $A B C D$ is a parallelogram and one of its interior angles is $90^{\circ}, A B C D$ is a rectangle.
2. Show that the diagonals of a square are equal and bisect each other at right angles.
Show Answer
Solution
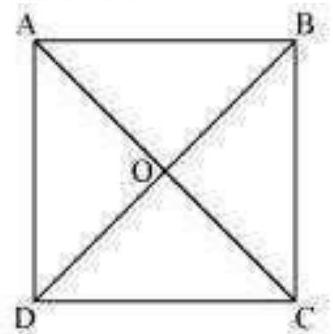
Let $A B C D$ be a square. Let the diagonals $A C$ and $B D$ intersect each other at a point $O$. To prove that the diagonals of a square are equal and bisect each other at right angles, we have to prove $A C=B D, O A=O C, O B=O D$, and $\angle A O B=90^{\circ}$.
In $\triangle A B C$ and $\triangle D C B$,
$A B=D C$ (Sides of a square are equal to each other)
$\angle ABC=\angle DCB(.$ All interior angles are of $90^{\circ}$ )
$B C=C B$ (Common side)
$\therefore \quad \triangle ABC \cong \triangle DCB$ (By SAS congruency)
$\therefore \quad AC=DB(By CPCT)$
Hence, the diagonals of a square are equal in length.
In $\triangle AOB$ and $\triangle COD$, $\angle AOB=\angle COD$ (Vertically opposite angles)
$\angle ABO=CDO$ (Alternate interior angles)
$A B=C D$ (Sides of a square are always equal)
$\angle \triangle AOB^{\angle} \triangle COD$ (By AAS congruence rule)
$\angle AO=CO$ and $OB=OD$ (By CPCT)
Hence, the diagonals of a square bisect each other.
In $\triangle AOB$ and $\triangle COB$,
As we had proved that diagonals bisect each other, therefore,
$AO=CO$
$A B=C B$ (Sides of a square are equal)
$BO=BO$ (Common)
$\angle \triangle AOB \triangle COB$ (By SSS congruency)
$\angle AOB=COOB(By CPCT)$
However, $\hat{A O B}+\angle C O B=180^{\circ}$ (Linear pair)
$\angle AOB=180^{\circ} 2$
$\angle AOB=90^{\circ}$
Hence, the diagonals of a square bisect each other at right angles.
3. Diagonal $\mathrm{AC}$ of a parallelogram $\mathrm{ABCD}$ bisects $\angle \mathrm{A}$ (see Fig. 8.11). Show that
(i) it bisects $\angle \mathrm{C}$ also,
(ii) $\mathrm{ABCD}$ is a rhombus.
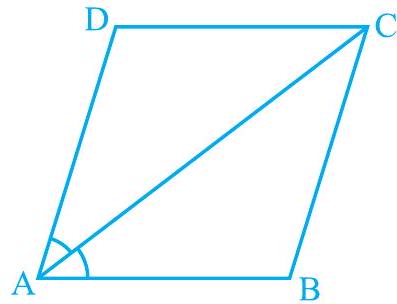
Fig. 8.11
Show Answer
Solution
(i) $A B C D$ is a parallelogram.
$\angle DAC=BCA$ (Alternate interior angles) ..
And, $B A C=D C A$ (Alternate interior angles) … (2) However, it is given that $A C$ bisects $\angle A$.
$\angle \angle DAC=\angle BAC \ldots$
From equations (1), (2), and (3), we obtain
$\angle D A C=B C A=B A €=\angle D C A$.
$\angle$ DCA $=B C A$
Hence, $A C$ bisects $C^{\circ}$.
(ii)From equation (4), we obtain
$\angle DAC=\angle DCA$
$\angle DA=DC$ (Side opposite to equal angles are equal)
However, $D A=B C$ and $A B=C D$ (Opposite sides of a parallelogram)
$\angle A B=B C=C D=D A$ Hence, $A B C D$
is a rhombus.
4. $\mathrm{ABCD}$ is a rectangle in which diagonal $\mathrm{AC}$ bisects $\angle \mathrm{A}$ as well as $\angle \mathrm{C}$. Show that:
(i) $\mathrm{ABCD}$ is a square
(ii) diagonal $\mathrm{BD}$ bisects $\angle \mathrm{B}$ as well as $\angle \mathrm{D}$.
Show Answer
Solution
(i) It is given that $A B C D$ is a rectangle.
$\angle \angle A=\angle C$
$ \begin{aligned} & \Rightarrow \frac{1}{2} \angle A=\frac{1}{2} \angle C \\ & \Rightarrow \angle DAC=\angle DCA \quad(AC \text{ bisects } \angle A \text{ and } \angle C) \end{aligned} $
$C D=D A$ (Sides opposite to equal angles are also equal)
However, $D A=B C$ and $A B=C D$ (Opposite sides of a rectangle are equal)
$\angle A B=B C=C D=D A$
$A B C D$ is a rectangle and all of its sides are equal.
Hence, $A B C D$ is a square.
(ii) Let us join BD.
In $\triangle B C D$,
$B C=C D$ (Sides of a square are equal to each other)
$\angle C D B=\mathbb{C} B D$ (Angles opposite to equal sides are equal)
However, $́ CDB=\angle ABD$ (Alternate interior angles for $A B | C D$ )
$\angle CBD=ABD$
$\angle BD$ bisects $B$.
Also, $C^{C} B D=A D B$ (Alternate interior angles for $B C | A D$ )
$\angle \angle CDB=A ABD \angle$
BD bisects b.
5. In parallelogram $A B C D$, two points $P$ and $Q$ are taken on diagonal $\mathrm{BD}$ such that $\mathrm{DP}=\mathrm{BQ}$ (see Fig. 8.12). Show that:
(i) $\triangle \mathrm{APD} \cong \triangle \mathrm{CQB}$
(ii) $\mathrm{AP}=\mathrm{CQ}$
(iii) $\triangle \mathrm{AQB} \cong \triangle \mathrm{CPD}$
(iv) $\mathrm{AQ}=\mathrm{CP}$
(v) APCQ is a parallelogram
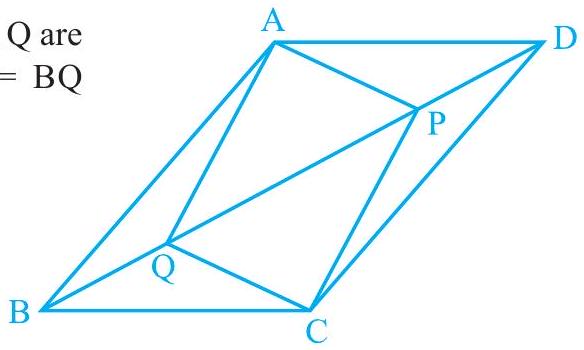
Fig. 8.12
Show Answer
Solution
(i) In $\triangle APD$ and $\triangle CQB$,
$\angle ADP=\angle CBQ$ (Alternate interior angles for $BC || AD$ )
$A D=C B$ (Opposite sides of parallelogram ABCD)
$DP=BQ$ (Given)
$\angle \triangle APD \angle \triangle CQB$ (Using SAS congruence rule) ii)
As we had observed that $\triangle APD \angle \triangle CQB,($
$\angle AP=CQ(CPCT)$
(iii) In $\triangle AQB$ and $\triangle CPD$,
$\angle ABQ=\angle CDP$ (Alternate interior angles for $AB || CD$ )
$A B=C D$ (Opposite sides of parallelogram ABCD)
$B Q=D P$ (Given)
$\angle \triangle AQB \angle \triangle CPD$ (Using SAS congruence rule) iv)
As we had observed that $\triangle AQB \angle \triangle CPD$, (
$\angle AQ=CP(CPCT)$
(v) From the result obtained in (ii) and (iv),
$AQ=CP$ and $AP=CQ$
Since opposite sides in quadrilateral APCQ are equal to each other, APCQ is a parallelogram.
6. $\mathrm{ABCD}$ is a parallelogram and $\mathrm{AP}$ and $\mathrm{CQ}$ are perpendiculars from vertices $\mathrm{A}$ and $\mathrm{C}$ on diagonal $\mathrm{BD}$ (see Fig. 8.13). Show that
(i) $\triangle \mathrm{APB} \cong \triangle \mathrm{CQD}$
(ii) $\mathrm{AP}=\mathrm{CQ}$
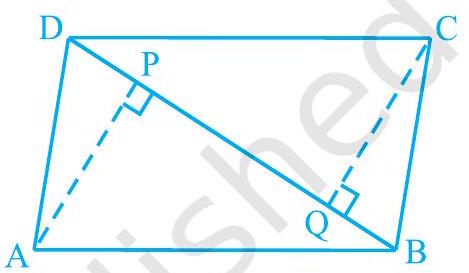
Fig. 8.13
Show Answer
Solution
(i) In $\triangle APB$ and $\triangle CQD$,
$\angle APB=\angle CQD(.$ Each $.90^{\circ})$
$A B=C D$ (Opposite sides of parallelogram $A B C D) \quad \angle A B P$
$=$ CDQ (Alternate interior angles for $A B || C D$ )
${ }^{\angle} \triangle APB \angle \triangle CQD$ (By AAS congruency)
(ii) By using the above result
$\triangle APB \angle \triangle CQD$, we obtain $A P=C Q(B y C P C T)$
7. $\mathrm{ABCD}$ is a trapezium in which $\mathrm{AB} || \mathrm{CD}$ and $\mathrm{AD}=\mathrm{BC}$ (see Fig. 8.14). Show that
(i) $\angle \mathrm{A}=\angle \mathrm{B}$
(ii) $\angle \mathrm{C}=\angle \mathrm{D}$
(iii) $\triangle \mathrm{ABC} \cong \triangle \mathrm{BAD}$
(iv) diagonal $\mathrm{AC}=$ diagonal $\mathrm{BD}$
[Hint: Extend $\mathrm{AB}$ and draw a line through $\mathrm{C}$ parallel to $\mathrm{DA}$ intersecting $\mathrm{AB}$ produced at $\mathrm{E}$.]
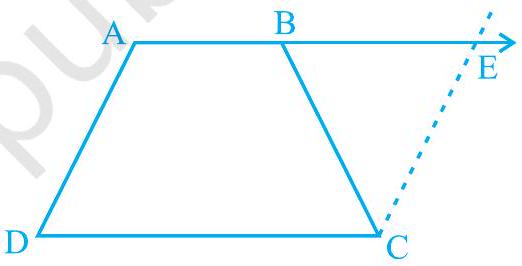
Fig. 8.14
Show Answer
Solution
Let us extend $A B$. Then, draw a line through $C$, which is parallel to $A D$, intersecting $A E$ at point $E$. It is clear that AECD is a parallelogram.
(i) $\quad AD=CE$ (Opposite sides of parallelogram AECD)
However, $A D=B C$ (Given)
Therefore, $BC=CE$
$\angle CEB=/ CBE$ (Angle opposite to equal sides are also equal)
Consider parallel lines AD and CE. AE is the transversal line for them.
$\angle A+C E B=180^{\circ}$ (Angles on the same side of transversal)
${ }^{\angle} A+C B E=180^{\circ}$ (Using the relation $\angle C E B=\angle C B E$ ) $\ldots(1)$
However, $\hat{B}+C B E=180^{\circ}$ (Linear pair angles) $\ldots$ (2)
From equations (1) and (2), we obtain $\angle A$
$=\angle B$
(ii) $\quad A B || C D$
$\angle A+D=180^{\circ}$ (Angles on the same side of the transversal)
Also, $C^{c}+B=180^{\circ}$ (Angles on the same side of the transversal)
$\angle A+D \leqq C+B$
However, $\grave{A}=B$ [Using the result obtained in (i) $] \angle C=$ D
(iii) In $\triangle A B C$ and $\triangle B A D$,
$A B=B A($ Common side)
$B C=A D$ (Given)
$\angle B=A$ (Proved before)
$\angle \triangle ABC \triangle BAD$ (SAS congruence rule) (iv) We had observed that, $\triangle ABC \angle \triangle BAD$
$\angle AC=BD(By CPCT)$





