Chapter 08 Quadrilaterals Exercise-02
EXERCISE 8.2
1. $A B C D$ is a quadrilateral in which $P, Q, R$ and $S$ are mid-points of the sides $\mathrm{AB}, \mathrm{BC}, \mathrm{CD}$ and $\mathrm{DA}$ (see Fig 8.20). AC is a diagonal. Show that :
(i) $\mathrm{SR} || \mathrm{AC}$ and $\mathrm{SR}=\frac{1}{2} \mathrm{AC}$
(ii) $\mathrm{PQ}=\mathrm{SR}$
(iii) $\mathrm{PQRS}$ is a parallelogram.
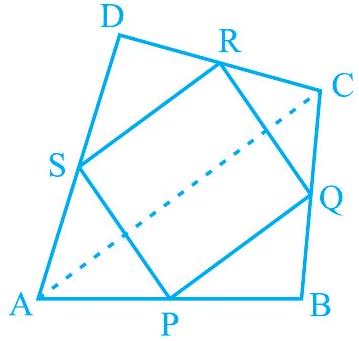
Fig. 8.20
Show Answer
Solution
(i) In $\triangle A D C, S$ and $R$ are the mid-points of sides $A D$ and $C D$ respectively. In a triangle, the line segment joining the mid-points of any two sides of the triangle is parallel to the third side and is half of it.
$\angle SR || AC$ and $SR=\frac{1}{2} AC$.
(ii) In $\triangle A B C, P$ and $Q$ are mid-points of sides $A B$ and $B C$ respectively. Therefore, by using mid-point theorem,
$P Q || A C$ and $P Q=\frac{1}{2} A C \ldots$
Using equations (1) and (2), we obtain
$PQ || SR$ and $PQ=SR \ldots$ (3) $\angle$
$P Q=S R$ (iii) From equation (3), we obtained
Clearly, one pair of opposite sides of quadrilateral PQRS is parallel and equal.
2. $A B C D$ is a rhombus and $P, Q, R$ and $S$ are the mid-points of the sides $A B, B C, C D$ and $D A$ respectively. Show that the quadrilateral $P Q R S$ is a rectangle.
Show Answer
Solution

b $\quad$ e
$\angle PQ || AC$ and $PQ=\stackrel{\frac{1}{2}<}{2}$
In $\triangle A D C$, In $\triangle A B C, P$ and $Q$ are the mid-points of sides $A B$ and $BC$ respectively.
AC (Using mid-point theorem) … (1)
$R$ and $S$ are the mid-points of $C D$ and $A D$ respectively. $RS || AC$ and $RS=\sqrt{\frac{1}{2}} AC$ (Using mid-point theorem)
From equations (1) and (2), we obtain
$P Q || R S$ and $P Q=R S$
Since in quadrilateral PQRS, one pair of opposite sides is equal and parallel to each other, it is a parallelogram.
Let the diagonals of rhombus $A B C D$ intersect each other at point $O$.
In quadrilateral OMQN,
$\because$
$M Q || ON \because(PQ || AC) \quad QN$
I| OM ( QR || BD)
Therefore, OMQN is a parallelogram.
$\angle \angle \quad \angle M Q N=N O M$
$\angle L \quad \angle PQR=NOM$
However, $\angle NOM=90^{\circ}$ (Diagonals of a rhombus are perpendicular to each other) $\angle$ $\angle PQR=90^{\circ}$
Clearly, PQRS is a parallelogram having one of its interior angles as $90^{\circ}$.
Hence, $P Q R S$ is a rectangle.
3. $A B C D$ is a rectangle and $P, Q, R$ and $S$ are mid-points of the sides $A B, B C, C D$ and $D A$ respectively. Show that the quadrilateral $P Q R S$ is a rhombus.
Show Answer
Solution

Let us join $A C$ and $B D$.
In $\triangle ABC$,
$P$ and $Q$ are the mid-points of $A B$ and $B C$ respectively. $\angle PQ || AC$ and $\frac{1}{2} PQ=\quad AC($ Mid-point theorem $) \ldots$ Similarly in
$\triangle ADC$,
$\frac{1}{2}$
$SR || AC$ and $SR=AC$ (Mid-point theorem) … (2)
Clearly, $PQ|| SR$ and $PQ=SR$
Since in quadrilateral PQRS, one pair of opposite sides is equal and parallel to each other, it is a parallelogram.
$\angle PS || QR$ and $PS=QR$ (Opposite sides of parallelogram) $\ldots(3)$
In $\triangle B C D, Q$ and $R$ are the mid-points of side $B C$ and $C D$ respectively.
$\angle QR || BD$ and $QR=\frac{1}{2} BD$ (Mid-point theorem) …
However, the diagonals of a rectangle are equal. /
$A C=B D \ldots(5)$
By using equation (1), (2), (3), (4), and (5), we obtain PQ
$=QR=SR=PS$ Therefore, $PQRS$ is a rhombus.
4. $\mathrm{ABCD}$ is a trapezium in which $\mathrm{AB} || \mathrm{DC}, \mathrm{BD}$ is a diagonal and $\mathrm{E}$ is the mid-point of $\mathrm{AD}$. A line is drawn through $E$ parallel to $A B$ intersecting $B C$ at $F$ (see Fig. 8.21). Show that $\mathrm{F}$ is the mid-point of $\mathrm{BC}$.
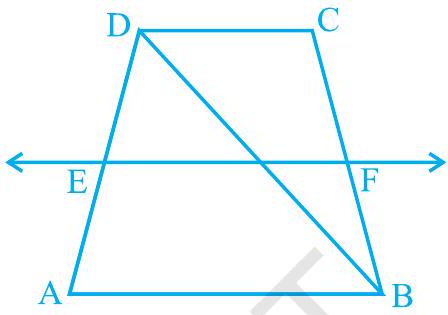
Fig. 8.21
Show Answer
Solution
Let $EF$ intersect $DB$ at $G$.

By converse of mid-point theorem, we know that a line drawn through the mid-point of any side of a triangle and parallel to another side, bisects the third side.
In $\triangle ABD$,
$E F || A B$ and $E$ is the mid-point of $A D$.
Therefore, $G$ will be the mid-point of $DB$.
As $E F|| A B$ and $A B|| C D$,
$\angle EF || CD$ (Two lines parallel to the same line are parallel to each other)
In $\triangle BCD, GF || CD$ and $G$ is the mid-point of line $BD$. Therefore, by using converse of mid-point theorem, $F$ is the mid-point of $BC$.
5. In a parallelogram $A B C D, E$ and $F$ are the mid-points of sides $\mathrm{AB}$ and $\mathrm{CD}$ respectively (see Fig. 8.22). Show that the line segments AF and $\mathrm{EC}$ trisect the diagonal $\mathrm{BD}$.

Fig. 8.22
Show Answer
Solution
$A B C D$ is a parallelogram.
$\angle A B | C D$
And hence, AE I| FC
Again, $A B=C D$ (Opposite sides of parallelogram ABCD)
$ _{A B} \frac{1}{2} CD $
$A E=F C(E$ and $F$ are mid-points of side $A B$ and $C D)$
In quadrilateral $A E C F$, one pair of opposite sides (AE and $C F$ ) is parallel and equal to each other. Therefore, AECF is a parallelogram. $\angle A F ||$ EC (Opposite sides of a parallelogram)
In $\triangle DQC, F$ is the mid-point of side $DC$ and $FP || CQ$ (as $AF || EC$ ). Therefore, by using the converse of mid-point theorem, it can be said that $P$ is the mid-point of
DQ.
$\angle DP=PQ \ldots(1)$
Similarly, in $\triangle A P B, E$ is the mid-point of side $A B$ and $E Q || A P$ (as $A F || E C$ ).
Therefore, by using the converse of mid-point theorem, it can be said that $Q$ is the mid-point of $P B$.
$\angle PQ=QB \ldots(2)$
From equations (1) and (2), DP
$=PQ=BQ$
Hence, the line segments $A F$ and $E C$ trisect the diagonal $B D$.
6. $\mathrm{ABC}$ is a triangle right angled at $\mathrm{C}$. A line through the mid-point $\mathrm{M}$ of hypotenuse $\mathrm{AB}$ and parallel to $\mathrm{BC}$ intersects $\mathrm{AC}$ at $\mathrm{D}$. Show that
(i) D is the mid-point of AC
(ii) $\mathrm{MD} \perp \mathrm{AC}$
(iii) $\mathrm{CM}=\mathrm{MA}=\frac{1}{2} \mathrm{AB}$
Show Answer
Solution

(i) In $\triangle A B C$,
It is given that $M$ is the mid-point of $A B$ and $M D || B C$.
Therefore, $D$ is the mid-point of $A C$. (Converse of mid-point theorem)
(ii) As DM || $CB$ and $AC$ is a transversal line for them, therefore,
$\angle MDC+\angle DCB=180^{\circ}$ (Co-interior angles)
$\angle MDC+90^{\circ}=180^{\circ}$
$\angle MDC=90^{\circ}$
$\angle M D A C$
(iii) Join MC.
In $\triangle AMD$ and $\triangle CMD$, $A D=C D$ ( $D$ is the mid-point of side $A C$ ) $\quad A D M=\angle C D M$ (Each 90)
$DM=DM$ (Common)
$\angle \triangle AMD \angle \triangle CMD$ (By SAS
Therefore, $A M=C M$ (By CPCT)

congruence rule)
However, $A M=\stackrel{\frac{1}{2}}{A B}$ (M is the mid-point of $.A B)^{\angle}$
Therefore, it fan be said that
$C M=A M={ }^{\frac{1}{2}} A B$





