Chapter 09 Circles Exercise-02
EXERCISE 9.2
1. Two circles of radii $5 \mathrm{~cm}$ and $3 \mathrm{~cm}$ intersect at two points and the distance between their centres is $4 \mathrm{~cm}$. Find the length of the common chord.
Show Answer
Solution
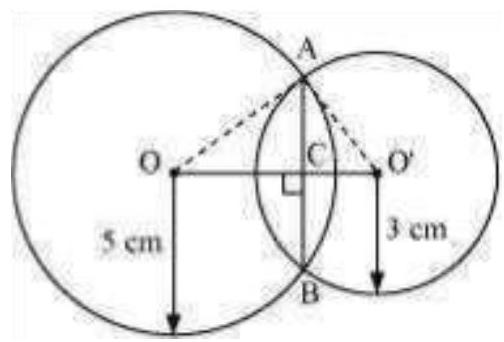
Let the radius of the circle centered at $O$ and $O^{\prime}$ be $5 cm$ and $3 cm$ respectively.
$OA=OB=5 cm$
$O^{\prime} A=O^{\prime} B=3 cm$
$O O$ ’ will be the perpendicular bisector of chord $A B$.
$\therefore A C=C B$
It is given that, $OO^{\prime}=4 cm$
Let $O C$ be $x$. Therefore, $O^{\prime} C$ will be $4-x$.
In $\triangle OAC$,
$OA^{2}=AC^{2}+OC^{2}$
$ \begin{aligned} & \Rightarrow \quad 5^{2}=A C^{2}+x^{2} \\ & \Rightarrow \quad 25-x^{2}=A C^{2} \ldots(1) \text{ In } \end{aligned} $
$\triangle O^{\prime} A C$,
$O^{\prime} A^{2}=A C^{2}+O^{\prime} C^{2}$
$\Rightarrow 3^{2}=A C^{2}+(4-x)^{2}$
$\Rightarrow 9=AC^{2}+16+x^{2}-8 x$
$\Rightarrow \quad AC^{2}=-x^{2}-7+8 x \ldots$
From equations (1) and (2), we obtain
$25-x^{2}=-x^{2}-7+8 x$
$8 x=32 x=4$
Therefore, the common chord will pass through the centre of the smaller circle i.e., O’ and hence, it will be the diameter of the smaller circle.
$A C^{2}=25-x^{2}=25-4^{2}=25-16=9$
$\therefore A C=3 m$
Length of the common chord $A B=2 A C=(2 \times 3) m=6 m$
2. If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Show Answer
Solution
Let $PQ$ and $RS$ be two equal chords of a given circle and they are intersecting each other at point $T$.
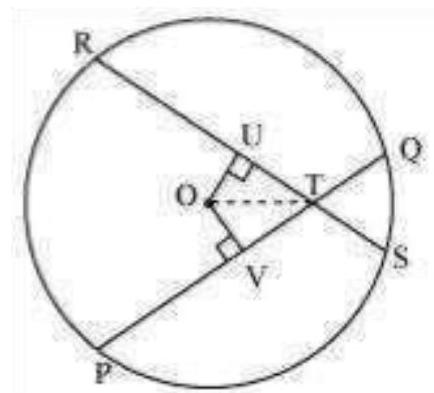
Draw perpendiculars OV and OU on these chords.
In $\triangle OVT$ and $\triangle OUT$,
$OV=OU$ (Equal chords of a circle are equidistant from the centre)
$\angle OVT=\angle OUT(.$ Each $.90^{\circ})$
OT $=$ OT (Common)
$\therefore \Delta OVT \approx \Delta OUT$ (RHS congruence rule) $\therefore VT=$ UT (By CPCT) … (1)
It is given that,
$ \begin{aligned} & PQ=RS \ldots(2) \\ & \frac{1}{2} PQ=\frac{1}{2} RS \\ & \Rightarrow \\ & \Rightarrow PV=RU \ldots(3) \end{aligned} $
On adding equations (1) and (3), we obtain $PV+VT=RU+UT$
$\Rightarrow PT=RT \ldots(4)$
On subtracting equation (4) from equation (2), we obtain
$P Q-P T=R S-R T$
$\Rightarrow QT=ST$
Equations (4) and (5) indicate that the corresponding segments of chords PQ and RS are congruent to each other.
3. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Show Answer
Solution
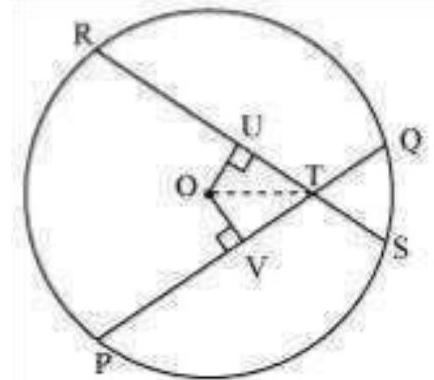
Let $PQ$ and $RS$ are two equal chords of a given circle and they are intersecting each other at point $T$.
Draw perpendiculars OV and OU on these chords.
In $\Delta OVT$ and $\Delta OUT$,
$OV=OU$ (Equal chords of a circle are equidistant from the centre)
$\angle OVT=\angle OUT(.$ Each $90^{\circ}$ )
OT $=$ OT (Common) $\therefore \triangle O V T$ AOUT (RHS congruence rule)
$\therefore$ ÓTV $=$ OfU (By CPCT)
Therefore, it is proved that the line joining the point of intersection to the centre makes equal angles with the chords.
4. If a line intersects two concentric circles (circles with the same centre) with centre $\mathrm{O}$ at $\mathrm{A}, \mathrm{B}, \mathrm{C}$ and $\mathrm{D}$, prove that $\mathrm{AB}=\mathrm{CD}$ (see Fig. 9.12).
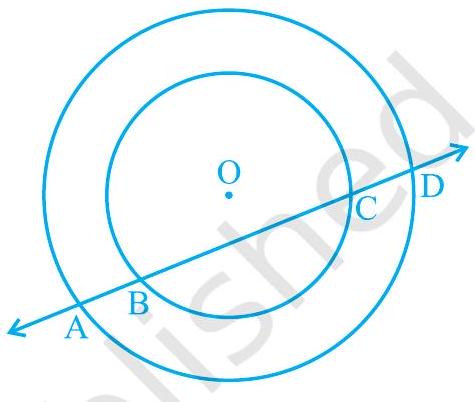
Fig. 9.12
Show Answer
Solution
Let us draw a perpendicular OM on line AD.
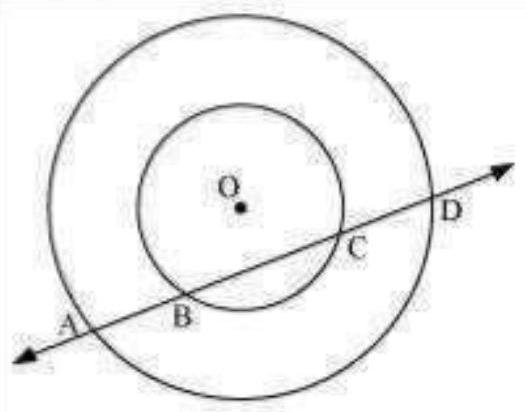
It can be observed that $BC$ is the chord of the smaller circle and $AD$ is the chord of the bigger circle.
We know that perpendicular drawn from the centre of the circle bisects the chord.
$\angle B M=M C \ldots$ (1) And, $A M=M D \ldots$ (2)
On subtracting equation (2) from (1), we obtain
$A M-B M=M D-M C$
$\angle AB=CD$
5. Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius $5 \mathrm{~m}$ drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is $6 \mathrm{~m}$ each, what is the distance between Reshma and Mandip?
Show Answer
Solution
Draw perpendiculars $OA$ and $OB$ on $RS$ and $SM$ respectively.
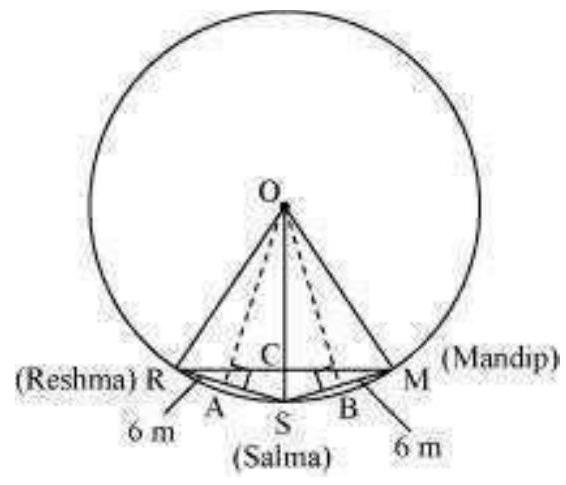
$ AR=AS=\frac{6}{2}=3 m $
$OR=OS=OM=5 m$. (Radii of the circle)
In $\triangle OAR$,
$OA^{2}+AR^{2}=OR^{2}$
$OA^{2}+(3 m)^{2}=(5 m)^{2}$
$OA^{2}=(25-9) m^{2}=16 m^{2}$
$OA=4 m$
ORSM will be a kite ( $O R=O M$ and $R S=S M)$. We know that the diagonals of a kite are perpendicular and the diagonal common to both the isosceles triangles is bisected by another diagonal.
$\angle \angle$
RCS will be of $90^{\circ}$ and $RC=CM$
$\frac{1}{2} \times OA \times RS$
Area of $\triangle ORS=$
$\frac{1}{2} \times RC \times OS=\frac{1}{2} \times 4 \times 6$
$RC \times 5=24$
$RC=4.8$
$RM=2 RC=2(4.8)=9.6$
Therefore, the distance between Reshma and Mandip is $9.6 m$.
6. A circular park of radius $20 \mathrm{~m}$ is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Show Answer
Solution
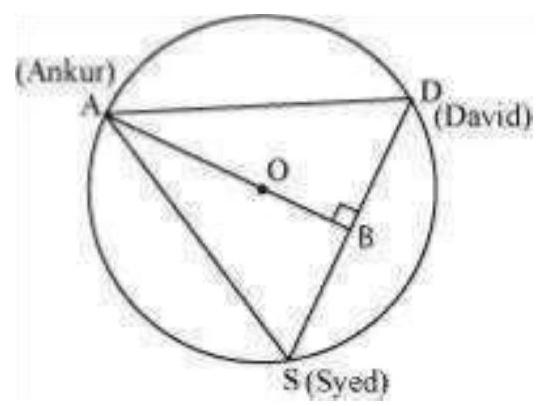
It is given that $A S=S D=D A$
Therefore, $\triangle ASD$ is an equilateral triangle. $OA($ radius) $=20 m$
Medians of equilateral triangle pass through the circum centre $(O)$ of the equilateral triangle ASD. We also know that medians intersect each other in the ratio 2: 1 . As
$A B$ is the median of equilateral triangle $A S D$, we can write
$\Rightarrow \frac{OA}{OB}=\frac{2}{1}$
$\Rightarrow \frac{20 m}{OB}=\frac{2}{1}$
$\Rightarrow OB=(\frac{20}{2}) m=10 m$
$\angle AB=OA+OB=(20+10) m=30 m$
In $\triangle ABD$,
$A D^{2}=A B^{2}+B D^{2}$
$A D^{2}=(30)^{2}+(\frac{A D}{2})^{2}$
$AD^{2}=900+\frac{1}{4} AD^{2}$
$\frac{3}{4} AD^{2}=900$
$AD^{2}=1200$
$AD=20 \sqrt{3}$
Therefore, the length of the string of each phone will be $20 \sqrt{3} m$.





