Chapter 10 Heron's Formula Exercise-01
EXERCISE 10.1
1. A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ’ $a$ ‘. Find the area of the signal board, using Heron’s formula. If its perimeter is $180 \mathrm{~cm}$, what will be the area of the signal board?
Show Answer
Solution
Side of traffic signal board $=a$
Perimeter of traffic signal board $=3 \times a$
$2 s=3 a \Rightarrow s=\frac{3}{2} a$
By Heron’s formula,
Area of triangle $=\sqrt{s(s-a)(s-b)(s-c)}$
Area of given triangle $=\sqrt{\frac{3}{2} a(\frac{3}{2} a-a)(\frac{3}{2} a-a)(\frac{3}{2} a-a)}$
$$ \begin{align} & =\sqrt{(\frac{3}{2} a)(\frac{a}{2})(\frac{a}{2})(\frac{a}{2})} \\ & =\frac{\sqrt{3}}{4} a^{2} \tag{1} \end{align} $$
Perimeter of traffic signal board $=180 cm$
Side of traffic signal board
$ (a)=(\frac{180}{3}) cm=60 cm $
Using equation (1), area of traffic signal board
$ =\frac{\sqrt{3}}{4}(60 cm)^{2} $
$=(\frac{3600}{4} \sqrt{3}) cm^{2}=900 \sqrt{3} cm^{2}$
2. The triangular side walls of a flyover have been used for advertisements. The sides of the walls are $122 \mathrm{~m}, 22 \mathrm{~m}$ and $120 \mathrm{~m}$ (see Fig. 10.6). The advertisements yield an earning of ₹ 5000 per $\mathrm{m}^{2}$ per year. A company hired one of its walls for 3 months. How much rent did it pay?
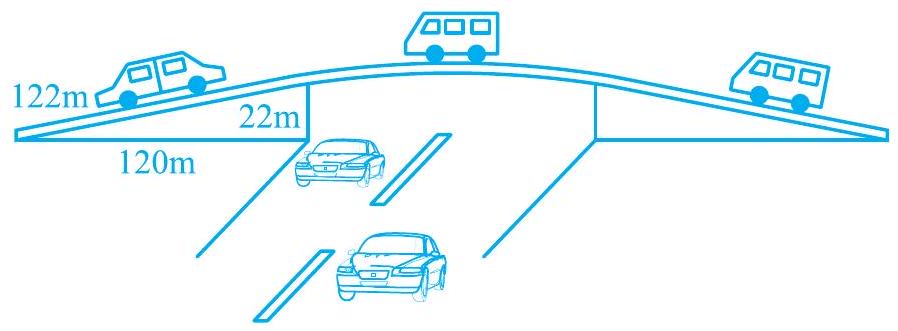
Fig. 10.6
Show Answer
Solution
The sides of the triangle (i.e., a, b, c) are of $122 m, 22 m$, and $120 m$ respectively.
Perimeter of triangle $=(122+22+120) m$
$2 s=264 m s=$
$132 m$
By Heron’s formula,
Area of triangle $=\sqrt{s(s-a)(s-b)(s-c)}$
Area of given triangle $=[\sqrt{132(132-122)(132-22)(132-120)}] m^{2}$
$ =[\sqrt{132(10)(110)(12)}] m^{2}=1320 m^{2} $
Rent of $1 m^{2}$ area per year $=$ Rs 5000
Rent of $1 m^{2}$ area per month $=Rs \frac{\frac{5000}{12}}{12}$
$Rs(\frac{5000}{12} \times 3 \times 1320)$
Rent of $1320 m^{2}$ area for 3 months $=$
$ Rs(\frac{5000}{12} \times 3 \times 1320) $
$=Rs(5000 \times 330)=Rs 1650000$
Therefore, the company had to pay Rs 1650000 .
3. There is a slide in a park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREENAND CLEAN” (see Fig. 10.7). If the sides of the wall are $15 \mathrm{~m}, 11 \mathrm{~m}$ and $6 \mathrm{~m}$, find the area painted in colour.

Fig. 10.7
Show Answer
Solution
Here $a=15 \mathrm{~m}, \mathrm{~b}=11 \mathrm{~m}, \mathrm{c}=6 \mathrm{~m}$ $$ \begin{aligned} & s=\frac{a+b+c}{2} \ & s=\frac{15+11+6}{2}=16 \mathrm{~m} \end{aligned} $$
Area of triangle $=\sqrt{s(s-a)(s-b)(s-c)}$ $$ \begin{aligned} & =\sqrt{16(16-15)(16-11)(16-6)} \\ & =\sqrt{16 \times 1 \times 5 \times 10} \\ & =20 \sqrt{2} \mathrm{~m}^2 \end{aligned} $$
Hence, the area painted in colour $=20 \sqrt{2} m^2$
4. Find the area of a triangle two sides of which are $18 \mathrm{~cm}$ and $10 \mathrm{~cm}$ and the perimeter is $42 \mathrm{~cm}$.
Show Answer
Solution
Let the third side of the triangle be $x$.
Perimeter of the given triangle $=42 cm$
$18 cm+10 cm+x=42 x=$
$14 cm$
$s=\frac{\text{ Perimeter }}{2}=\frac{42 cm}{2}=21 cm$
By Heron’s formula.
$ \begin{aligned} & \text{ Area of a triangle }=\sqrt{s(s-a)(s-b)(s-c)} \\ & \begin{aligned} \text{ Area of the given triangle } & =(\sqrt{21(21-18)(21-10)(21-14)}) cm^{2} \\ & =(\sqrt{21(3)(11)(7)}) cm^{2} \\ & =21 \sqrt{11} cm^{2} \end{aligned} \end{aligned} $
5. Sides of a triangle are in the ratio of $12: 17: 25$ and its perimeter is $540 \mathrm{~cm}$. Find its area.
Show Answer
Solution
Let the common ratio between the sides of the given triangle be $x$.
Therefore, the side of the triangle will be $12 x, 17 x$, and $25 x$.
Perimeter of this triangle $=540 cm$
$12 x+17 x+25 x=540 c m$
$54 x=540 cm x=$
$10 cm$
Sides of the triangle will be $120 cm, 170 cm$, and $250 cm$.
$s=\frac{\text{ Perimeter of triangle }}{2}=\frac{540 cm}{2}=270 cm$
By Heron’s formula,
$ \begin{aligned} \text{ Area of triangle } & =\sqrt{s(s-a)(s-b)(s-c)} \\ & =[\sqrt{270(270-120)(270-170)(270-250)}] cm^{2} \\ & =[\sqrt{270 \times 150 \times 100 \times 20}] cm^{2} \\ & =9000 cm^{2} \end{aligned} $
Therefore, the area of this triangle is $9000 cm^{2}$.
6. An isosceles triangle has perimeter $30 \mathrm{~cm}$ and each of the equal sides is $12 \mathrm{~cm}$. Find the area of the triangle.
Show Answer
Solution
Let the third side of this triangle be $x$.
Perimeter of triangle $=30 cm$
$12 cm+12 cm+x=30 cm$
$ \begin{aligned} & x=6 cm \\ & s=\frac{\text{ Perimeter of triangle }}{2}=\frac{30 cm}{2}=15 cm \end{aligned} $
By Heron’s formula,
$ \begin{aligned} \text{ Area of triangle } & =\sqrt{s(s-a)(s-b)(s-c)} \\ & =[\sqrt{15(15-12)(15-12)(15-6)}] cm^{2} \\ & =[\sqrt{15(3)(3)(9)}] cm^{2} \\ & =9 \sqrt{15} cm^{2} \end{aligned} $





