Solution

(i) Radius ( $r$ ) of cone $=6 cm$

Height (h) of cone $=7 cm$

Volume of cone

$ =\frac{1}{3} \pi r^{2} h $

$=[\frac{1}{3} \times \frac{22}{7} \times(6)^{2} \times 7] cm^{3}$

$=(12 \times 22) cm^{3}$

$=264 cm^{3}$

Therefore, the volume of the cone is $264 cm^{3}$.

(ii) Radius ( $r$ ) of cone $=3.5 cm$

Height (h) of cone $=12 cm$

Volume of cone

$ =\frac{1}{3} \pi r^{2} h $

$=[\frac{1}{3} \times \frac{22}{7} \times(3.5)^{2} \times 12] cm^{3}$

$=(\frac{1}{3} \times 22 \times \frac{1}{2} \times 3.5 \times 12) cm^{3}$

$=154 cm^{3}$

Therefore, the volume of the cone is $154 cm^{3}$.

Solution

(i) Radius ( $r$ ) of cone $=7 cm$

Slant height (I) of cone $=25 cm$

Height (h) of cone $=\sqrt{l^{2}-r^{2}}$

$=(\sqrt{25^{2}-7^{2}}) cm$

$=24 cm$

Volume of cone $=\frac{1}{3} \pi r^{2} h$

$=(\frac{1}{3} \times \frac{22}{7} \times(7)^{2} \times 24) cm^{3}$

$=(154 \times 8) cm^{3}$

$=1232 cm^{3}$

Therefore, capacity of the conical vessel

$=(\frac{1232}{1000})$ litres $(1.$ litre $.=1000 cm^{3})$

$=1.232$ litres

(ii) Height (h) of cone $=12 cm$

Slant height $(I)$ of cone $=13 cm$

Radius $(r.$ ) of cone $=\sqrt{l^{2}-h^{2}}$

$=(\sqrt{13^{2}-12^{2}}) cm$

$=5 cm$

Volume of cone $=\frac{1}{3} \pi r^{2} h$

$ \begin{aligned} & =[\frac{1}{3} \times \frac{22}{7} \times(5)^{2} \times 12] cm^{3} \\ & =(4 \times \frac{22}{7} \times 25) cm^{3} \\ & =(\frac{2200}{7}) cm^{3} \end{aligned} $

Therefore, capacity of the conical vessel

$ \begin{aligned} &(\frac{2200}{7000}) \text{ litres }(1 \text{ litre }=1000 cm^{3}) \\ &= \frac{11}{35} \text{ litres } \\ & \text{ Question 3: } \end{aligned} $

Solution

Height $(h)$ of cone $=15 cm$

Let the radius of the cone be $r$. Volume of cone

$=1570 cm^{3}$

$\frac{1}{3} \pi r^{2} h=1570 cm^{3}$

$\Rightarrow(\frac{1}{3} \times 3.14 \times r^{2} \times 15) cm=1570 cm^{3}$

$\Rightarrow r^{2}=100 cm^{2}$

$\Rightarrow r=10 cm$

Therefore, the radius of the base of cone is $10 cm$.

Solution

Height (h) of cone $=9 cm$

Let the radius of the cone be $r$.

Volume of cone $=48 cm^{3}$

$\Rightarrow \frac{1}{3} \pi r^{2} h=48 \pi cm^{3}$

$\Rightarrow(\frac{1}{3} \pi r^{2} \times 9) cm=48 \pi cm^{3}$

$\Rightarrow r^{2}=16 cm^{2}$

$\Rightarrow r=4 cm$

Diameter of base $=2 r=8 cm$

Solution

Radius ( $r$ ) of pit

$ =(\frac{3.5}{2}) m=1.75 m $

Height $(h)$ of pit $=$ Depth of pit $=12 m$

Volume of pit

$ =\frac{1}{3} \pi r^{2} h $

$=[\frac{1}{3} \times \frac{22}{7} \times(1.75)^{2} \times 12] cm^{3}$

$=38.5 m^{3}$

Thus, capacity of the pit $=(38.5 \times 1)$ kilolitres $=38.5$ kilolitres

Solution

(i) Radius of cone $=(\frac{28}{2}) cm=14 cm$

Let the height of the cone be $h$. Volume of cone

$=9856 cm^{3}$

$ \begin{aligned} & \Rightarrow \frac{1}{3} \pi r^{2} h=9856 cm^{3} \\ & \Rightarrow[\frac{1}{3} \times \frac{22}{7} \times(14)^{2} \times h] cm^{2}=9856 cm^{3} \end{aligned} $

$h=48 cm$

Therefore, the height of the cone is $48 cm$.

(ii) Slant height (I) of cone $=\sqrt{r^{2}+h^{2}}$

$=[\sqrt{(14)^{2}+(48)^{2}}] cm$

$=[\sqrt{196+2304}] cm$

$=50 cm$

Therefore, the slant height of the cone is $50 cm$.

(iii) $CSA$ of cone $=nrl$

$=(\frac{22}{7} \times 14 \times 50) cm^{2}$

$=2200 cm^{2}$

Therefore, the curved surface area of the cone is $2200 cm^{2}$.

Solution

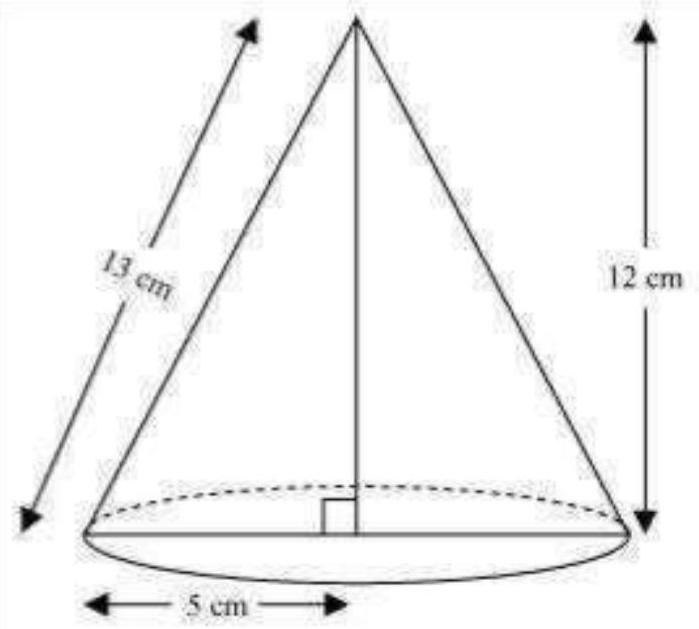
When right-angled $\triangle A B C$ is revolved about its side $12 cm$, a cone with height $(h)$ as 12 $cm$, radius ( $r$ ) as $5 cm$, and slant height (I) $13 cm$ will be formed.

$ =\frac{1}{3} \pi r^{2} h $

Volume of cone

$=[\frac{1}{3} \times \pi \times(5)^{2} \times 12] cm^{3}$

$=100 \pi cm^{3}$

Therefore, the volume of the cone so formed is $100 n cm^{3}$.

Solution

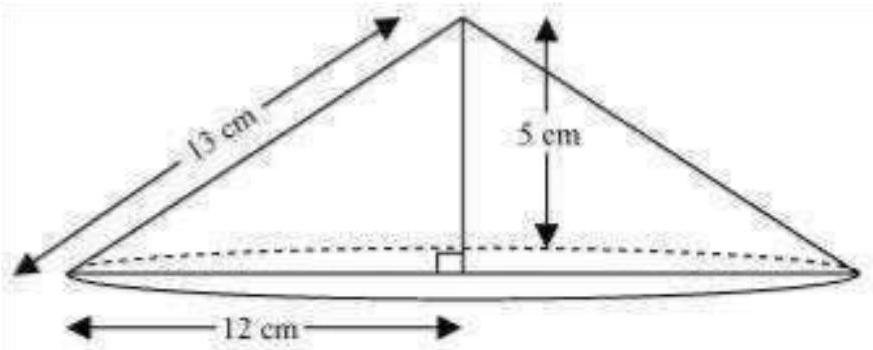
When right-angled $\triangle A B C$ is revolved about its side $5 cm$, a cone will be formed having radius ( $r$ ) as $12 cm$, height ( $h$ ) as $5 cm$, and slant height $(I)$ as $13 cm$.

$ \begin{aligned} & \qquad=\frac{1}{3} \pi r^{2} h \\ & \text{ Volume of cone } \\ & =[\frac{1}{3} \times \pi \times(12)^{2} \times 5] cm^{3} \\ & =240 \pi cm^{3} \\ & \qquad=\frac{100 \pi}{240 \pi} \\ & \text{ Reauired ratio } \\ & =\frac{5}{12}=5: 12 \end{aligned} $

Solution

Radius ( $r$ ) of heap

$ =(\frac{10.5}{2}) m=5.25 m $

Height ( $h$ ) of heap $=3 m$

Volume of heap

$ =\frac{1}{3} \pi r^{2} h $

$=(\frac{1}{3} \times \frac{22}{7} \times(5.25)^{2} \times 3) m^{3}$

$=86.625 m^{3}$

Therefore, the volume of the heap of wheat is $86.625 m^{3}$.

Area of canvas required $=$ CSA of cone

$ \begin{aligned} & =\pi r l=\pi r \sqrt{r^{2}+h^{2}} \\ & =[\frac{22}{7} \times 5.25 \times \sqrt{(5.25)^{2}+(3)^{2}}] m^{2} \\ & =(\frac{22}{7} \times 5.25 \times 6.05) m^{2} \\ & =99.825 m^{2} \end{aligned} $

Therefore, $99.825 m^{2}$ canvas will be required to protect the heap from rain.

Find the volume of a sphere whose radius is

(i) $7 cm$ (ii) $0.63 m$

Assume $.\pi=\frac{22}{7}]$