Chapter 10 Circles Exercise-02
EXERCISE 10.2
In Q. 1 to 3, choose the correct option and give justification.
1. From a point $\mathrm{Q}$, the length of the tangent to a circle is $24 \mathrm{~cm}$ and the distance of $\mathrm{Q}$ from the centre is $25 \mathrm{~cm}$. The radius of the circle is
(A) $7 \mathrm{~cm}$
(B) $12 \mathrm{~cm}$
(C) $15 \mathrm{~cm}$
(D) $24.5 \mathrm{~cm}$
Show Answer
Solution
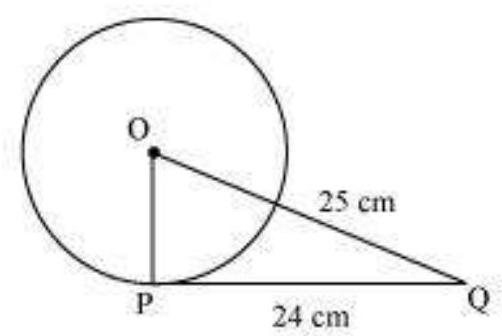
Let $O$ be the centre of the circle.
Given that,
$OQ=25 cm$ and $PQ=24 cm$
As the radius is perpendicular to the tangent at the point of contact,
Therefore, $OP \perp PQ$
Applying Pythagoras theorem in $\triangle OPQ$, we obtain
$OP^{2}+PQ^{2}=OQ^{2}$
$OP^{2}+24^{2}=25^{2}$
$OP^{2}=625-576$
$OP^{2}=49$
$OP=7$
Therefore, the radius of the circle is $7 cm$.
Hence, alternative (A) is correct.
2. In Fig. 10.11, if $\mathrm{TP}$ and $\mathrm{TQ}$ are the two tangents to a circle with centre $\mathrm{O}$ so that $\angle \mathrm{POQ}=110^{\circ}$, then $\angle \mathrm{PTQ}$ is equal to
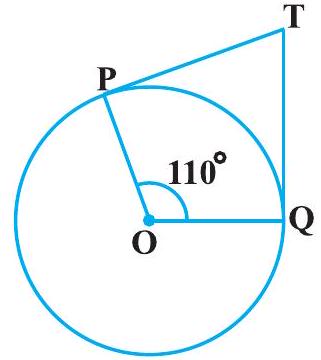
Fig. 10.11
(A) $60^{\circ}$
(B) $70^{\circ}$
(C) $80^{\circ}$
(D) $90^{\circ}$
Show Answer
Solution
It is given that TP and TQ are tangents.
Therefore, radius drawn to these tangents will be perpendicular to the tangents.
Thus, $OP \perp TP$ and $OQ \perp TQ$
$\angle OPT=90^{\circ}$
$\angle OQT=90^{\circ}$
In quadrilateral POQT,
Sum of all interior angles $=360^{\circ}$
$\angle OPT+\angle POQ+\angle OQT+\angle PTQ=360^{\circ}$
$\Rightarrow 90^{\circ}+110^{\circ}+90^{\circ}+\angle PTQ=360^{\circ}$
$\Rightarrow \angle PTQ=70^{\circ}$
Hence, alternative (B) is correct.
3. If tangents $\mathrm{PA}$ and $\mathrm{PB}$ from a point $\mathrm{P}$ to a circle with centre $\mathrm{O}$ are inclined to each other at angle of $80^{\circ}$, then $\angle \mathrm{POA}$ is equal to
(A) $50^{\circ}$
(B) $60^{\circ}$
(C) $70^{\circ}$
(D) $80^{\circ}$
Show Answer
Solution
It is given that PA and PB are tangents.
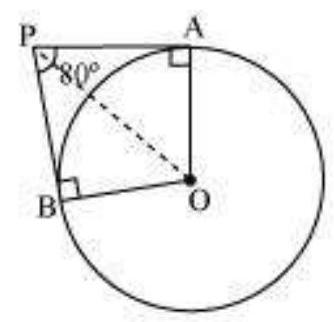
Therefore, the radius drawn to these tangents will be perpendicular to the tangents.
Thus, $OA \perp PA$ and $OB \perp PB$
$\angle OBP=90^{\circ}$
$\angle OAP=90^{\circ}$
In AOBP,
Sum of all interior angles $=360^{\circ}$
$ \begin{aligned} & \angle OAP+\angle APB+\angle PBO+\angle BOA=360^{\circ} \\ & 90^{\circ}+80^{\circ}+90^{\circ}+\angle BOA=360^{\circ} \\ & \angle BOA=100^{\circ} \end{aligned} $
In $\triangle OPB$ and $\triangle OPA$,
$A P=B P($ Tangents from a point $)$
$OA=OB$ (Radii of the circle)
$OP=OP$ (Common side)
Therefore, $\triangle OPB \cong \triangle OPA$ (SSS congruence criterion)
$A \rightarrow B, P \rightarrow P, O \rightarrow O$
And thus, $\angle POB=\angle POA$
$\angle POA=\dfrac{1}{2} \angle AOB=\dfrac{100^{\circ}}{2}=50^{\circ}$
Hence, alternative (A) is correct.
4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Show Answer
Solution
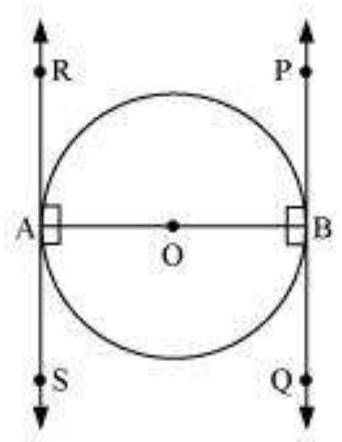
Let $A B$ be a diameter of the circle. Two tangents $P Q$ and $R S$ are drawn at points $A$ and $B$ respectively. Radius drawn to these tangents will be perpendicular to the tangents.
Thus, $OA \perp RS$ and $OB \perp PQ$
$\angle OAR=90^{\circ}$
$\angle OAS=90^{\circ}$
$\angle OBP=90^{\circ}$
$\angle OBQ=90^{\circ}$
It can be observed that $\angle OAR=\angle OBQ$ (Alternate interior angles)
$\angle OAS=\angle OBP$ (Alternate interior angles)
Since alternate interior angles are equal, lines $P Q$ and $R S$ will be parallel.
5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Show Answer
Solution
Let us consider a circle with centre $O$. Let $AB$ be a tangent which touches the circle at $P$.

We have to prove that the line perpendicular to $A B$ at $P$ passes through centre $O$. We shall prove this by contradiction method.
Let us assume that the perpendicular to $A B$ at $P$ does not pass through centre $O$. Let it pass through another point $O^{\prime}$. Join OP and O’P.
As perpendicular to $A B$ at $P$ passes through $O^{\prime}$, therefore,
$\angle O^{\prime} PB=90^{\circ}$
$O$ is the centre of the circle and $P$ is the point of contact. We know the line joining the centre and the point of contact to the tangent of the circle are perpendicular to each other.
$\therefore \angle OPB=90^{\circ}$..
Comparing equations (1) and (2), we obtain
$\angle O ’ PB=\angle OPB$..
From the figure, it can be observed that,
$\angle O$ ‘PB $<\angle OPB$…
Therefore, $\angle O O^{\prime} PB=\angle OPB$ is not possible. It is only possible, when the line O’P coincides with OP.
Therefore, the perpendicular to $A B$ through $P$ passes through centre $O$.
6. The length of a tangent from a point $A$ at distance $5 \mathrm{~cm}$ from the centre of the circle is 4 $\mathrm{cm}$. Find the radius of the circle.
Show Answer
Solution
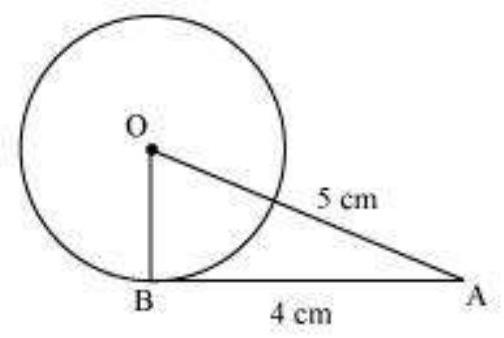
Let us consider a circle centered at point $O$.
$A B$ is a tangent drawn on this circle from point $A$.
Given that,
$O A=5 cm$ and $A B=4 cm$
In $\triangle ABO$,
$OB \perp AB$ (Radius $\perp$ tangent at the point of contact)
Applying Pythagoras theorem in $\triangle A B O$, we obtain
$AB^{2}+BO^{2}=OA^{2}$
$4^{2}+BO^{2}=5^{2}$
$16+BO^{2}=25$
$BO^{2}=9$
$BO=3$
Hence, the radius of the circle is $3 cm$.
7. Two concentric circles are of radii $5 \mathrm{~cm}$ and $3 \mathrm{~cm}$. Find the length of the chord of the larger circle which touches the smaller circle.
Show Answer
Solution
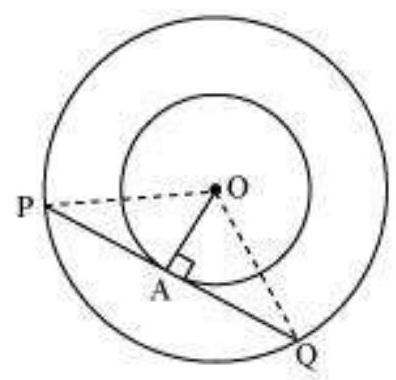
Let the two concentric circles be centered at point $O$. And let $PQ$ be the chord of the larger circle which touches the smaller circle at point $A$. Therefore, $PQ$ is tangent to the smaller circle.
$OA \perp PQ(As OA$ is the radius of the circle)
Applying Pythagoras theorem in $\triangle OAP$, we obtain
$OA^{2}+AP^{2}=OP^{2}$
$3^{2}+AP^{2}=5^{2}$
$9+AP^{2}=25$
$AP^{2}=16$
$AP=4$
In $\triangle OPQ$,
Since $OA \perp PQ$,
$AP=AQ$ (Perpendicular from the center of the circle bisects the chord)
$\therefore PQ=2 AP=2 \times 4=8$
Therefore, the length of the chord of the larger circle is $8 cm$.
8. A quadrilateral $A B C D$ is drawn to circumscribe a circle (see Fig. 10.12). Prove that
$$ \mathrm{AB}+\mathrm{CD}=\mathrm{AD}+\mathrm{BC} $$
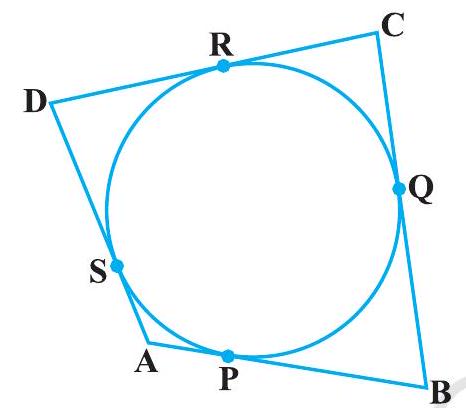
Fig. 10.12
Show Answer
Solution
It can be observed that
DR $=$ DS (Tangents on the circle from point D) $CR=CQ$ (Tangents on the circle from point C) …
$B P=B Q($ Tangents on the circle from point $B)$
AP $=$ AS (Tangents on the circle from point A)
Adding all these equations, we obtain
$DR+CR+BP+AP=DS+CQ+BQ+AS$
$(D R+C R)+(B P+A P)=(D S+A S)+(C Q+B Q)$
$C D+A B=A D+B C$
9. In Fig. 10.13, $\mathrm{XY}$ and $\mathrm{X}^{\prime} \mathrm{Y}^{\prime}$ are two parallel tangents to a circle with centre $\mathrm{O}$ and another tangent $A B$ with point of contact $C$ intersecting $X Y$ at $A$ and $X^{\prime} Y^{\prime}$ at $B$. Prove that $\angle \mathrm{AOB}=90^{\circ}$.

Fig. 10.13
Show Answer
Solution
Let us join point $O$ to $C$.

In $\triangle OPA$ and $\triangle OCA$,
$OP=OC$ (Radii of the same circle)
$A P=A C($ Tangents from point $A)$
$AO=AO$ (Common side)
$\triangle OPA \cong \triangle OCA$ (SSS congruence criterion)
Therefore, $P \rightarrow C, A \rightarrow A, O \rightarrow O$
$\angle POA=\angle COA \ldots$ (i)
Similarly, $\triangle OQB \cong \triangle OCB$ $\angle QOB=\angle COB \ldots$
Since POQ is a diameter of the circle, it is a straight line.
Therefore, $\angle POA+\angle COA+\angle COB+\angle QOB=180^{\circ}$
From equations (i) and (ii), it can be observed that
$2 \angle COA+2 \angle COB=180^{\circ}$
$\angle COA+\angle COB=90^{\circ}$
$\angle A O B=90^{\circ}$
10. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Show Answer
Solution
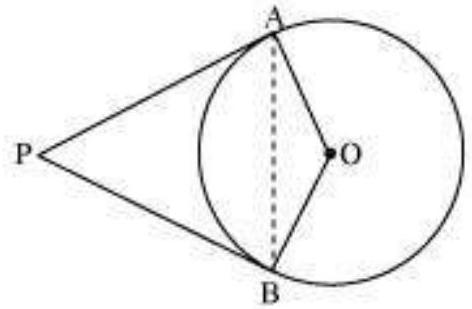
Let us consider a circle centered at point $O$. Let $P$ be an external point from which two tangents $PA$ and $PB$ are drawn to the circle which are touching the circle at point $A$ and $B$ respectively and $A B$ is the line segment, joining point of contacts $A$ and $B$ together such that it subtends $\angle A O B$ at center $O$ of the circle.
It can be observed that
$OA$ (radius) $\perp PA$ (tangent)
Therefore, $\angle OAP=90^{\circ}$
Similarly, OB (radius) $\perp$ PB (tangent)
$\angle OBP=90^{\circ}$
In quadrilateral OAPB,
Sum of all interior angles $=360^{\circ}$
$\angle OAP+\angle APB+\angle PBO+\angle BOA=360^{\circ}$
$90^{\circ}+\angle APB+90^{\circ}+\angle BOA=360^{\circ}$
$\angle APB+\angle BOA=180^{\circ}$
Hence, it can be observed that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
11. Prove that the parallelogram circumscribing a circle is a rhombus.
Show Answer
Solution
Since $A B C D$ is a parallelogram,
$A B=C D$…(1)
$B C=A D \ldots(2)$
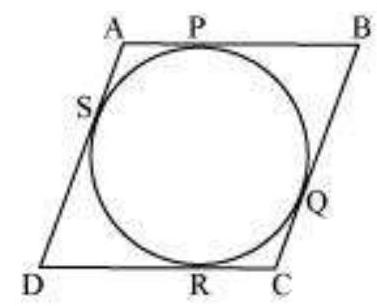
It can be observed that
DR $=$ DS (Tangents on the circle from point D)
$CR=CQ$ (Tangents on the circle from point C)
$BP=BQ$ (Tangents on the circle from point $B$ )
AP = AS (Tangents on the circle from point A)
Adding all these equations, we obtain
$DR+CR+BP+AP=DS+CQ+BQ+AS$
$(DR+CR)+(BP+AP)=(DS+AS)+(CQ+BQ)$
$C D+A B=A D+B C$
On putting the values of equations (1) and (2) in this equation, we obtain
$2 AB=2 BC$
$AB=BC$
Comparing equations (1), (2), and (3), we obtain
$AB=BC=CD=DA$
Hence, $A B C D$ is a rhombus.
12. A triangle $A B C$ is drawn to circumscribe a circle of radius $4 \mathrm{~cm}$ such that the segments $\mathrm{BD}$ and DC into which $B C$ is divided by the point of contact $\mathrm{D}$ are of lengths $8 \mathrm{~cm}$ and $6 \mathrm{~cm}$ respectively (see Fig. 10.14). Find the sides $A B$ and AC.
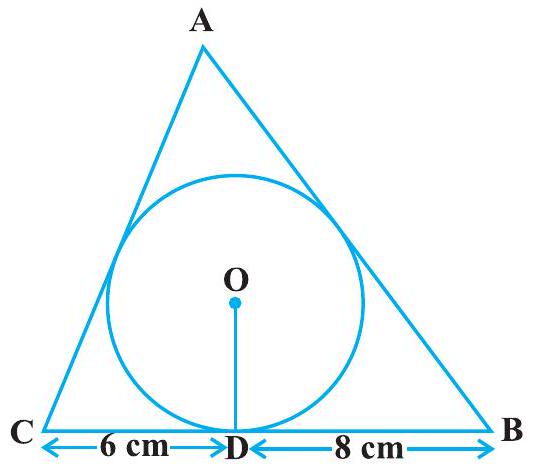
Fig. 10.14
Show Answer
Solution
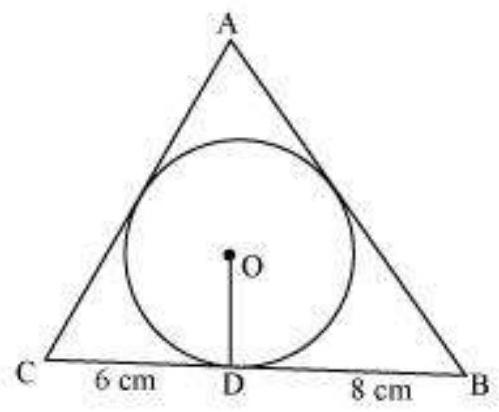
Let the given circle touch the sides $A B$ and $A C$ of the triangle at point $E$ and $F$ respectively and the length of the line segment AF be $x$.
In $\triangle ABC$,
$CF=CD=6 cm$ (Tangents on the circle from point $C$ )
$BE=BD=8 cm$ (Tangents on the circle from point $B$ )
$AE=AF=x($ Tangents on the circle from point $A)$
$AB=AE+EB=x+8$
$BC=BD+DC=8+6=14$
$CA=CF+FA=6+x$
$2 s=A B+B C+C A$
$=x+8+14+6+x$
$=28+2 x$
$s=14+x$
$ \text{ Area of } \begin{aligned} \Delta ABC & =\sqrt{s(s-a)(s-b)(s-c)} \\ & =\sqrt{{14+x}{(14+x)-14}{(14+x)-(6+x)}{(14+x)-(8+x)}} \\ & =\sqrt{(14+x)(x)(8)(6)} \\ & =4 \sqrt{3(14 x+x^{2})} \end{aligned} $
Area of $\triangle OBC=\dfrac{1}{2} \times OD \times BC=\dfrac{1}{2} \times 4 \times 14=28$
Area of $\triangle OCA=\dfrac{1}{2} \times OF \times AC=\dfrac{1}{2} \times 4 \times(6+x)=12+2 x$
Area of $\triangle OAB=\dfrac{1}{2} \times OE \times AB=\dfrac{1}{2} \times 4 \times(8+x)=16+2 x$
Area of $\triangle ABC=$ Area of $\triangle OBC+$ Area of $\triangle OCA+$ Area of $\triangle OAB$
$4 \sqrt{3(14 x+x^{2})}=28+12+2 x+16+2 x$
$\Rightarrow 4 \sqrt{3(14 x+x^{2})}=56+4 x$
$\Rightarrow \sqrt{3(14 x+x^{2})}=14+x$
$\Rightarrow 3(14 x+x^{2})=(14+x)^{2}$
$\Rightarrow 42 x+3 x^{2}=196+x^{2}+28 x$
$\Rightarrow 2 x^{2}+14 x-196=0$
$\Rightarrow x^{2}+7 x-98=0$
$\Rightarrow x^{2}+14 x-7 x-98=0$
$\Rightarrow x(x+14)-7(x+14)=0$
$\Rightarrow(x+14)(x-7)=0$
Either $x+14=0$ or $x-7=0$
Therefore, $x=-14$ and 7
However, $x=-14$ is not possible as the length of the sides will be negative.
Therefore, $x=7$
Hence, $AB=x+8=7+8=15 cm$
$CA=6+x=6+7=13 cm$
13. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Show Answer
Solution
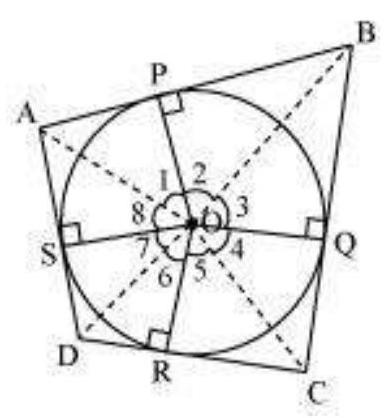
Let $A B C D$ be a quadrilateral circumscribing a circle centered at $O$ such that it touches the circle at point $P, Q, R, S$. Let us join the vertices of the quadrilateral $A B C D$ to the center of the circle.
Consider $\triangle OAP$ and $\triangle OAS$,
AP $=$ AS (Tangents from the same point)
$OP=OS$ (Radii of the same circle)
$OA=OA$ (Common side)
$\Delta OAP \cong \triangle OAS$ (SSS congruence criterion)
And thus, $\angle POA=\angle AOS$
$\angle 1=\angle 8$
Similarly,
$\angle 2=\angle 3$
$\angle 4=\angle 5$
$\angle 6=\angle 7$
$\angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6+\angle 7+\angle 8=360^{\circ}$
$(\angle 1+\angle 8)+(\angle 2+\angle 3)+(\angle 4+\angle 5)+(\angle 6+\angle 7)=360^{\circ}$
$2 \angle 1+2 \angle 2+2 \angle 5+2 \angle 6=360^{\circ}$
$2(\angle 1+\angle 2)+2(\angle 5+\angle 6)=360^{\circ}$
$(\angle 1+\angle 2)+(\angle 5+\angle 6)=180^{\circ}$
$\angle AOB+\angle COD=180^{\circ}$
Similarly, we can prove that $\angle BOC+\angle DOA=180^{\circ}$
Hence, opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.





