Solution

We have, $y^{2}=9 x, y=3 x$

Solving the two equations, we have

$(3 x)^{2}=9 x$

$\Rightarrow \quad 9 x^{2}-9 x=0 \Rightarrow 9 x(x-1)=0$

$\therefore \quad x=0,1$

Area of the shaded region

$=area($ region $OAB)-area(\triangle OAB)$

$=-\int_0^{1} y_l \cdot d x=\int_0^{1} \sqrt{9 x} d x-\int_0^{1} 3 x d x$

$=3 \int_0^{1} \sqrt{x} d x-3 \int_0^{1} x d x=3 \times \dfrac{2}{3}[x^{3 / 2}]_0^{1}-3[\dfrac{x^{2}}{2}]_0^{1}$

$=2[(1)^{3 / 2}-0]-\dfrac{3}{2}[(1)^{2}-0]=2(1)-\dfrac{3}{2}(1)=2-\dfrac{3}{2}=\dfrac{1}{2}$ sq. units

Hence, the required area $=\dfrac{1}{2}$ sq. units.

Solution

We are given that: $x^{2}=2 p y \ldots(i)$

and $y^{2}=2 p x \ldots(ii)$

From eqn. (i) we get $y=\dfrac{x^{2}}{2 p}$

Putting the value of $y$ in eqn.(ii) we have

$ \begin{aligned} & (\dfrac{x^{2}}{2 p})^{2}=2 p x \Rightarrow \dfrac{x^{4}}{4 p^{2}}=2 p x \\ & \Rightarrow x^{4}=8 p^{3} x \Rightarrow x^{4}-8 p^{3} x=0 \\ & \Rightarrow x(x^{3}-8 p^{3})=0 \\ &\therefore x=0,2 p \end{aligned} $

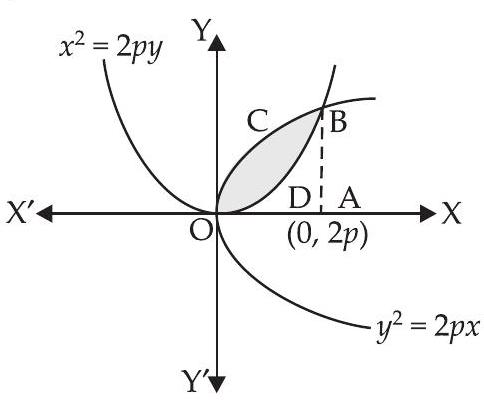
$ \begin{aligned} & \text{ Required area }=\text{ Area of the region }(\text{ OCBA - ODBA) } \\ & =\int_0^{2 p} \sqrt{2 p x} d x-\int_0^{2 p} \dfrac{x^{2}}{2 p} d x=\sqrt{2 p} \int_0^{2 p} \sqrt{x} d x-\dfrac{1}{2 p} \int_0^{2 p} x^{2} d x \\ & =\sqrt{2 p} \cdot \dfrac{2}{3}[x^{3 / 2}]_0^{2 p}-\dfrac{1}{2 p} \cdot \dfrac{1}{3}[x^{3}]_0^{2 p} \\ & =\dfrac{2 \sqrt{2}}{3} \sqrt{p}[(2 p)^{3 / 2}-0]-\dfrac{1}{6 p}[(2 p)^{3}-0] \\ & =\dfrac{2 \sqrt{2}}{3} \sqrt{p} \cdot 2 \sqrt{2} p^{\dfrac{3}{2}}-\dfrac{1}{6 p} \cdot 8 p^{3} \\ & =\dfrac{8}{3} \cdot p^{2}-\dfrac{8}{6} p^{2}=\dfrac{8}{6} p^{2}=\dfrac{4}{3} p^{2} \text{ sq. units } \end{aligned} $

Hence, the required area $=\dfrac{4}{3} p^{2}$ sq. units.

Solution

We are given that: $y=x^{3}, y=x+6$ and $x=0$

Solving $y=x^{3}$ and $y=x+6$, we get

$x+6 =x^{3}$

$\Rightarrow x^{3}-x-6 =0$

$\Rightarrow x^{2}(x-2)+2 x(x-2)+3(x-2) =0$

$\Rightarrow (x-2)(x^{2}+2 x+3) =0$

$x^{2}+2 x+3=0 \text{ has no real roots. } $

$\therefore x=2$

$\therefore$ Required area of the shaded region

$ \begin{aligned} & =\int_0^{2}(x+6) d x-\int_0^{2} x^{3} d x \\ & =[\dfrac{x^{2}}{2}+6 x]_0^{2}-\dfrac{1}{4}[x^{4}]_0^{2} \end{aligned} $

$ \begin{aligned} & =(\dfrac{4}{2}+12)-(0+0)-\dfrac{1}{4}[(2)^{4}-0] \\ & =14-\dfrac{1}{4} \times 16=14-4=10 \text{ sq. units. } \end{aligned} $

Solution

We have $y^{2}=4 x$ and $x^{2}=4 y$.

$ \begin{aligned} y & =\dfrac{x^{2}}{4} \\ \Rightarrow \quad(\dfrac{x^{2}}{4})^{2} & =4 x \end{aligned} $

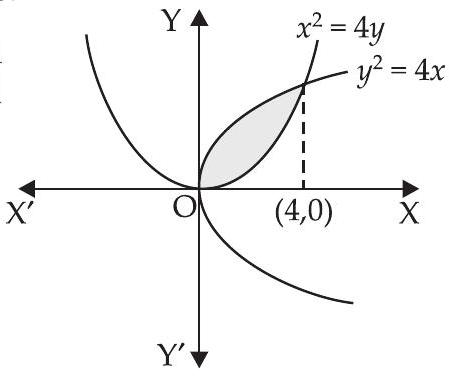
$ \begin{aligned} & \Rightarrow \quad \dfrac{x^{4}}{16}=4 x \\ & \Rightarrow \quad x^{4}=64 x \Rightarrow x^{4}-64 x=0 \\ & \Rightarrow \quad x(x^{3}-64)=0 \\ & \therefore x=0, x=4 \end{aligned} $

Required area $=\int_0^{4} \sqrt{4 x} d x-\int_0^{4} \dfrac{x^{2}}{4} d x=2 \int_0^{4} \sqrt{x} d x-\dfrac{1}{4} \int_0^{4} x^{2} d x$

$ \begin{aligned} & =2 \cdot \dfrac{2}{3}[x^{3 / 2}]_0^{4}-\dfrac{1}{4} \cdot \dfrac{1}{3}[x^{3}]_0^{4} \\ & =\dfrac{4}{3}[(4)^{3 / 2}-0]-\dfrac{1}{12}[(4)^{3}-0]=\dfrac{4}{3}[8]-\dfrac{1}{12}[64] \\ & =\dfrac{32}{3}-\dfrac{16}{3}=\dfrac{16}{3} \text{ sq. units } \end{aligned} $

Hence, the required area $=\dfrac{16}{3}$ sq. units.

Solution

Given that: $\quad y^{2}=9 x \ldots(i)$

and $\quad y=x \ldots(ii)$

Solving eqns. (i) and (ii) we have

$ \begin{aligned} x^{2} =9 x\\ \Rightarrow x^{2}-9 x=0 \\ \Rightarrow x(x-9) =0 \\ \therefore x=0,9 \end{aligned} $

Required area

$ \begin{aligned} & =\int_0^{9} \sqrt{9 x} d x-\int_0^{9} x d x=3 \int_0^{9} \sqrt{x} d x-\int_0^{9} x d x \\ & =3 \cdot \dfrac{2}{3}[x^{3 / 2}]_0^{9}-\dfrac{1}{2}[x^{2}]_0^{9} \\ & =2[(9)^{3 / 2}-0]-\dfrac{1}{2}[(9)^{2}-0] \\ & =2(27)-\dfrac{1}{2}(81)=54-\dfrac{81}{2}=\dfrac{108-81}{2} \\ & =\dfrac{27}{2} \text{ sq. units } \end{aligned} $

Hence, the required area $=\dfrac{27}{2}$ sq. units.

Solution

Here, $x^{2}=y$ and $y=x+2$

$\therefore \quad x^{2}=x+2$

$\Rightarrow \quad x^{2}-x-2=0$

$\Rightarrow \quad x^{2}-2 x+x-2=0$

$\Rightarrow \quad x(x-2)+1(x-2)=0$

$\Rightarrow \quad(x-2)(x+1)=0$

$\therefore x=-1,2$

Graph of $y=x+2$

$ \begin{array}{|c|c|c|} \hline x & 0 & -2 \\ \hline y & 2 & 0 \\ \hline \end{array} $

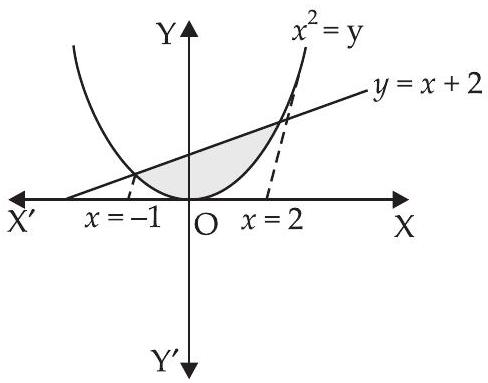
Area of the required region

$ \begin{aligned} & =\int _{-1}^{2}(x+2) d x-\int _{-1}^{2} x^{2} d x=[\dfrac{x^{2}}{2}+2 x] _{-1}^{2}-\dfrac{1}{3}[x^{3}] _{-1}^{2} \\ & =[(\dfrac{4}{2}+4)-(\dfrac{1}{2}-2)]-\dfrac{1}{3}[8-(-1)] \\ & =(6+\dfrac{3}{2})-\dfrac{1}{3}(9)=\dfrac{15}{2}-3=\dfrac{9}{2} \text{ sq. units } \end{aligned} $

Hence, the required area $=\dfrac{9}{2}$ sq. units.

Solution

Here,

$ y^{2}=8 x \text{ and } x=2 $

$ y^{2}=8(2)=16$

$ \therefore \quad y= \pm 4 $

Required area

$=2 \int_0^{2} \sqrt{8 x} d x=2 \times 2 \sqrt{2} \int_0^{2} \sqrt{x} d x$

$=4 \sqrt{2} \times \dfrac{2}{3}[x^{3 / 2}]_0^{2}$

$=\dfrac{8 \sqrt{2}}{3}[(2)^{3 / 2}]=\dfrac{8 \sqrt{2}}{3} \times 2 \sqrt{2}=\dfrac{32}{3}$ sq. units

Hence, the area of the region $=\dfrac{32}{3}$ sq. units.

Solution

Given that ${(x, 0): y=\sqrt{4-x^{2}}}$

$ \begin{matrix} \Rightarrow & y^{2}=4-x^{2} \\ \Rightarrow & x^{2}+y^{2}=4 \text{ which is a circle. } \end{matrix} $

Required area

$ =2 \cdot \int_0^{2} \sqrt{4-x^{2}} d x $

[Since circle is symmetrical about $y$-axis]

$ \begin{aligned} & =2 \cdot \int_0^{2} \sqrt{(2)^{2}-x^{2}} d x \\ & =2 \cdot[\dfrac{x}{2} \sqrt{4-x^{2}}+\dfrac{4}{2} \sin ^{-1} \dfrac{x}{2}]_0^{2} \\ & =2[(\dfrac{2}{2} \sqrt{4-4}+2 \sin ^{-1}(1))-(0+0)] \\ & =2[2 \cdot \dfrac{\pi}{2}]=2 \pi \text{ sq. units } \end{aligned} $

Hence, the required area $=2 \pi$ sq. units.

Solution

Given the curves $y=2 \sqrt{x}, x=0$ and $x=1$.

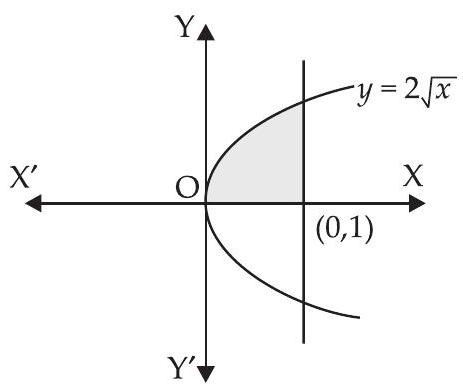
$ \begin{aligned} \text{ Required area } & =\int_0^{1}(2 \sqrt{x}) d x \\ & =2 \times \dfrac{2}{3}[x^{3 / 2}]_0^{1} \\ & =\dfrac{4}{3}[(1)^{3 / 2}-0] \\ & =\dfrac{4}{3} \text{ sq. units } \end{aligned} $

Hence, required area $=\dfrac{4}{3}$ sq. units.

Solution

Given that: $2 y=5 x+7, x$-axis, $x=2$ and $x=8$.

Let us draw the graph of $2 y=5 x+7 \Rightarrow y=\dfrac{5 x+7}{2}$

$ \begin{array}{|c|c|c|} \hline x & 1 & -1 \\ \hline y & 6 & 1 \\ \hline \end{array} $

Area of the required shaded region

$=\int_2^{8}(\dfrac{5 x+7}{2}) d x=\dfrac{1}{2}[\dfrac{5}{2} x^{2}+7 x]_2^{8}$

$=\dfrac{1}{2}[\dfrac{5}{2}(64-4)+7(8-2)]$

$=\dfrac{1}{2}[\dfrac{5}{2} \times 60+7 \times 6]=\dfrac{1}{2}[150+42]$

$=\dfrac{1}{2} \times 192=96$ sq. units

Hence, the required area $=96$ sq. units.

Solution

Here, we have $y=\sqrt{x-1}$

$\Rightarrow \quad y^{2}=x-1$ (Parabola)

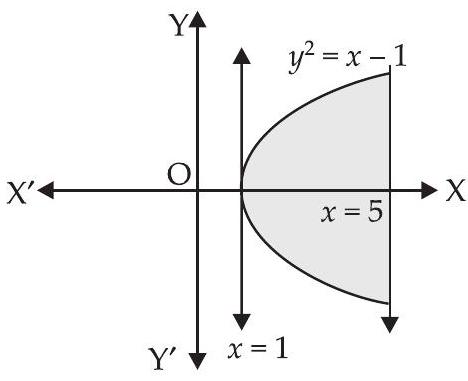
Area of the required region

$=\int_1^{5} \sqrt{x-1} d x$

$=\dfrac{2}{3}[(x-1)^{3 / 2}]_1^{5}$

$=\dfrac{2}{3}[(5-1)^{3 / 2}-0]=\dfrac{2}{3} \times(4)^{3 / 2}$

$=\dfrac{2}{3} \times 8=\dfrac{16}{3}$ sq. units

Hence, the required area $=\dfrac{16}{3}$ sq. units.

Solution

Here, we are given $y=\sqrt{a^{2}-x^{2}}$

$ \begin{matrix} \Rightarrow & y^{2}=a^{2}-x^{2} \\ \Rightarrow & x^{2}+y^{2}=a^{2} \end{matrix} $

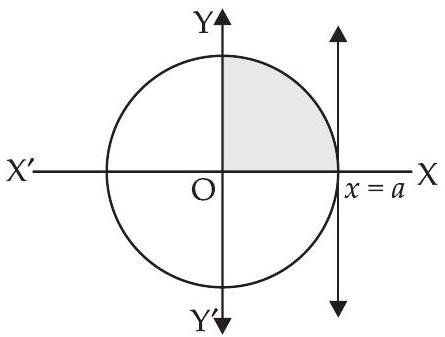
Area of the shaded region

$=2[(1)^{3 / 2}-0]-\dfrac{3}{2}[(1)^{2}-0]$

$=[\dfrac{x}{2} \sqrt{a^{2}-x^{2}}+\dfrac{a^{2}}{2} \sin ^{-1} \dfrac{x}{a}]_0^{a}$

$ \begin{aligned} & =[\dfrac{a}{2} \sqrt{a^{2}-a^{2}}+\dfrac{a^{2}}{2} \sin ^{-1} \dfrac{a}{a}-0-0] \\ & =\dfrac{a^{2}}{2} \sin ^{-1}(1)=\dfrac{a^{2}}{2} \cdot \dfrac{\pi}{2}=\dfrac{\pi a^{2}}{4} \end{aligned} $

Hence, the required area $=\dfrac{\pi a^{2}}{4}$ sq. units.

Solution

We are given the equations of curve $y=\sqrt{x}$ and line $y=x$.

Solving $y=\sqrt{x} \Rightarrow y^{2}=x$ and $y=x$, we get

$ \begin{aligned} x^{2} & =x \Rightarrow x^{2}-x=0 \\ \Rightarrow \quad x(x-1) & =0\\ \therefore x=0,1 \end{aligned} $

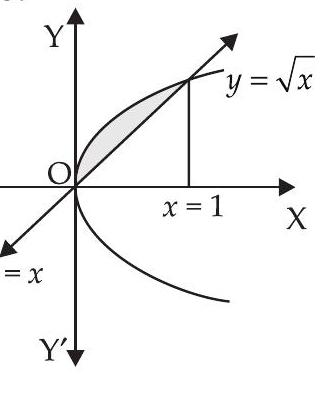
Required area of the shaded region

$ \begin{aligned} & =\int_0^{1} \sqrt{x} d x-\int_0^{1} x d x \\ & =\dfrac{2}{3}[x^{3 / 2}]_0^{1}-\dfrac{1}{2}[x^{2}]_0^{1} \\ & =\dfrac{2}{3}[(1)^{3 / 2}-0]-\dfrac{1}{2}[(1)^{2}-0] \\ & =\dfrac{2}{3}-\dfrac{1}{2} \Rightarrow \dfrac{4-3}{6} \Rightarrow \dfrac{1}{6} \text{ sq. units } \end{aligned} $

Hence, the required area $=\dfrac{1}{6}$ sq. units.

Solution

We are given that $y=-x^{2}$ or $x^{2}=-y$ and the line $x+y+2=0$

Solving the two equations, we get

$x-x^{2}+2 =0$

$\Rightarrow x^{2}-x-2 =0$

$\Rightarrow x^{2}-2 x+x-2 =0$

$\Rightarrow x(x-2)+1(x-2) =0$

$\Rightarrow (x-2)(x+1) =0$

$\therefore x =-1,2$

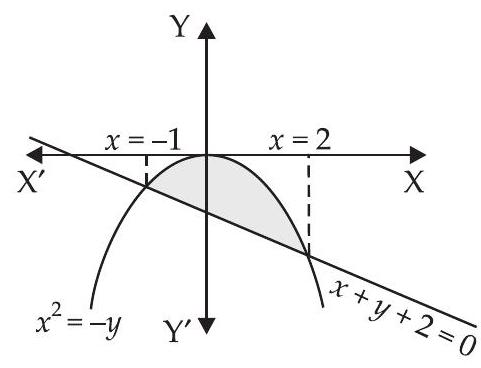
Area of the required shaded region

$=|\int _{-1}^{2}(-x-2) d x-\int _{-1}^{2}-x^{2} d x|$

$\Rightarrow \quad |-[\dfrac{x^{2}}{2}+2 x] _{-1}^{2} +\dfrac{1}{3}[x^{3}] _{-1}^{2}|$

$\Rightarrow \quad |-[(\dfrac{4}{2}+4)-(\dfrac{1}{2}-2)]+\dfrac{1}{3}(8+1)|$

$\Rightarrow \quad |-(6+\dfrac{3}{2})+\dfrac{1}{3}(9)|\Rightarrow|-\dfrac{15}{2}+3|$

$\Rightarrow \quad |\dfrac{-15+6}{2}|=|\dfrac{-9}{2}|=\dfrac{9}{2} \text{ sq. units }$

Solution

Given equation of the curves are for $ y = \sqrt{x} $ and $ x = 2y + 3 $ in the first quadrant.

On solving both the equation for $ y $, we get

$ \begin{aligned} & y = \sqrt{2y + 3} \ & \Rightarrow y^2 = 2y + 3 \ & \Rightarrow y^2 - 2y - 3 = 0 \ & \Rightarrow y^2 - 3y + y - 3 = 0 \ & \Rightarrow y(y - 3) + 1(y - 3) = 0 \ & \Rightarrow (y + 1)(y - 3) = 0 \ & \Rightarrow y = -1, 3 \end{aligned} $

$\therefore$ Required area of shaded region,

$ \begin{aligned} A &= \int_{0}^{3} (2y + 3 - y^2) , dy = \left[ \frac{2y^2}{2} + 3y - \frac{y^3}{3} \right]_{0}^{3} \ &= \left[ \frac{18}{2} + 9 - 9 - 0 \right] \ &= 9 \text{ sq units.} \end{aligned} $

Solution

Equations of the curves are given by

$$ \begin{equation*} x^{2}+y^{2}=4 x \qquad…(i) \end{equation*} $$

$$ \begin{equation*} \text{ and } \quad y^{2}=2 x \qquad…(ii) \end{equation*} $$

$ \begin{matrix} \Rightarrow & x^{2}-4 x+y^{2}=0 \\ \Rightarrow & x^{2}-4 x+4-4+y^{2}=0 \\ \Rightarrow & (x-2)^{2}+y^{2}=4 \end{matrix} $

Clearly it is the equation of a circle having its centre $(2,0)$ and radius 2 .

Solving $x^{2}+y^{2}=4 x$ and $y^{2}=2 x$

$ x^{2}+2 x=4 x $

$\Rightarrow x^{2}+2 x-4 x=0$

$\Rightarrow \quad x^{2}-2 x=0$

$\Rightarrow \quad x(x-2)=0$

$\therefore \quad x=0,2$

Area of the required region

$=2[\int_0^{2} \sqrt{4-(x-2)^{2}} d x-\int_0^{2} \sqrt{2 x} d x]$

[ $\therefore$ Parabola and circle both are symmetrical about $x$-axis.]

$=2[\dfrac{x-2}{2} \sqrt{4-(x-2)^{2}}+\dfrac{4}{2} \sin ^{-1} \dfrac{x-2}{2}]_0^{2}-2 \cdot \sqrt{2} \cdot \dfrac{2}{3}[x^{3 / 2}]_0^{2}$

$=2[(0+0)-(0+2 \sin ^{-1}(-1)]-\dfrac{4 \sqrt{2}}{3}[2^{3 / 2}-0].$

$=-2 \times 2 \cdot(-\dfrac{\pi}{2})-\dfrac{4 \sqrt{2}}{3} \cdot 2 \sqrt{2}$

$=2 \pi-\dfrac{16}{3}=2(\pi-\dfrac{8}{3})$ sq.units

Hence, the required area $=2(\pi-\dfrac{8}{3})$ sq. units.

Solution

Equation of the curves is given by

$y=\sin x$ between $x=0$ and $x=2 \pi$.

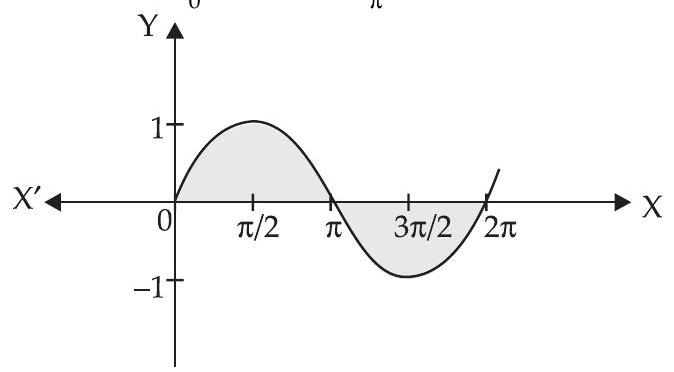
Required area $=\int_0^{\pi} \sin x d x+\int _{\pi}^{2 \pi}|\sin x| d x$

$ \begin{aligned} & =-[\cos x]_0^{\pi}+|(-\cos x)| _{\pi}^{2 \pi}=-[\cos \pi-\cos 0]+[\cos 2 \pi-\cos \pi] \\ & =-[-1-1]+[1+1]=2+2=4 \text{ sq. units } \end{aligned} $

Solution

The coordinates of the vertices of $\triangle ABC$ are given by $A(-1,1)$, B $(0,5)$ and $C(3,2)$.

Equation of $AB$ is $

$y-1=\dfrac{5-1}{0+1}(x+1)$

$\Rightarrow y-1 =4 x+4$

$\therefore y =4 x+4+1 \Rightarrow y=4 x+5 \qquad…(1)$

Equation of $BC\ $ is $ \quad y-5=\dfrac {2-5}{3-0}(x-0)$

$ \Rightarrow \quad y-5=-x $

$ \begin{aligned} \therefore \quad y=5-x \qquad…(ii) \end{aligned} $

Equation of $CA$ is

$ \begin{aligned} y-1 & =\dfrac{2-1}{3+1}(x+1) \\ \Rightarrow \quad y-1 & =\dfrac{1}{4} x+\dfrac{1}{4} \Rightarrow y=\dfrac{1}{4} x+\dfrac{1}{4}+1 \\ \therefore \quad y & =\dfrac{1}{4} x+\dfrac{5}{4}=\dfrac{1}{4}(5+x) \end{aligned} $

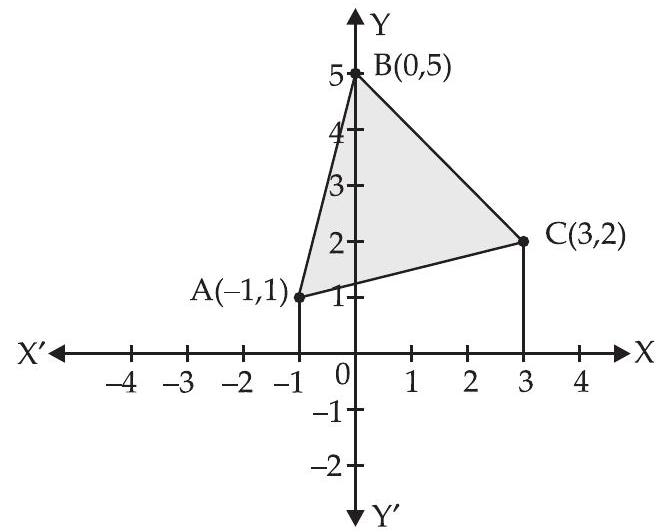
Area of $\triangle ABC$

$ \begin{aligned} & =\int _{-1}^{0}(4 x+5) d x+\int_0^{3}(5-x) d x-\int _{-1}^{3} \dfrac{1}{4}(5+x) d x \\ & =\dfrac{4}{2}[x^{2}] _{-1}^{0}+5[x] _{-1}^{0}+5[x]_0^{3}-\dfrac{1}{2}[x^{2}]_0^{3}-\dfrac{1}{4}[5 x+\dfrac{x^{2}}{2}] _{-1}^{3} \end{aligned} $

$ \begin{aligned} & =2(0-1)+5(0+1)+5(3-0)-\dfrac{1}{2}(9-0) \\ & -\dfrac{1}{4}[(15+\dfrac{9}{2})-(-5+\dfrac{1}{2})] \\ & =-2+5+15-\dfrac{9}{2}-\dfrac{1}{4}(\dfrac{39}{2}+\dfrac{9}{2}) \\ & =18-\dfrac{9}{2}-\dfrac{1}{4} \times \dfrac{48}{2}=18-\dfrac{9}{2}-6=12-\dfrac{9}{2}=\dfrac{15}{2} \text{ sq. units } \end{aligned} $

Hence, the required area $=\dfrac{15}{2}$ sq. units.

Solution

Given that:

${(x, y): y^{2} \leq 6 a x.$ and $.x^{2}+y^{2} \leq 16 a^{2}}$

Equation of Parabola is

$$ \begin{equation*} y^{2}=6 a x \qquad…(i) \end{equation*} $$

and equation of circle is

$$ \begin{equation*} x^{2}+y^{2} \leq 16 a^{2} \qquad…(ii) \end{equation*} $$

Solving eqns. (i) and (ii) we get

$ \begin{matrix} \Rightarrow & x^{2}+6 a x-16 a^{2}=0 \\ \Rightarrow & x^{2}+8 a x-2 a x-16 a^{2}=0 \\ \Rightarrow & x(x+8 a)-2 a(x+8 a)=0 \\ \Rightarrow & (x+8 a)(x-2 a)=0 \end{matrix} $

$\therefore x=2 a$ and $x=-8 a$. (Rejected as it is out of region)

Area of the required shaded region

$ \begin{aligned} & =2[\int_0^{2 a} \sqrt{6 a x} d x+\int _{2 a}^{4 a} \sqrt{16 a^{2}-x^{2}} d x] \\ & =2[\sqrt{6 a} \int_0^{2 a} \sqrt{x} d x+\int _{2 a}^{4 a} \sqrt{(4 a)^{2}-x^{2}} d x] \\ & =2 \sqrt{6 a} \cdot \dfrac{2}{3} \cdot[x^{3 / 2}]_0^{2 a}+2[\dfrac{x}{2} \sqrt{(4 a)^{2}-x^{2}}+\dfrac{16 a^{2}}{2} \sin ^{-1} \dfrac{x}{4 a}] _{2 a}^{4 a} \\ & =\dfrac{4 \sqrt{6}}{3} \cdot \sqrt{a}[(2 a)^{3 / 2}-0]+[x \sqrt{(4 a)^{2}-x^{2}}+16 a^{2} \sin ^{-1} \dfrac{x}{4 a}] _{2 a}^{4 a} \end{aligned} $

$ \begin{aligned} & =\dfrac{4 \sqrt{6}}{3} \sqrt{a} \cdot 2 \sqrt{2} \cdot a^{3 / 2}+[0+16 a^{2} \sin ^{-1}(\dfrac{4 a}{4 a})-2 a \sqrt{16 a^{2}-4 a^{2}}-16 a^{2} \sin ^{-1} \dfrac{2 a}{4 a}] \\ & =\dfrac{8 \sqrt{12}}{3} a^{2}+[16 a^{2} \cdot \sin ^{-1}(1)-2 a \sqrt{12 a^{2}}-16 a^{2} \sin ^{-1} \dfrac{1}{2}] \\ & =\dfrac{16 \sqrt{3}}{3} a^{2}+[16 a^{2} \cdot \dfrac{\pi}{2}-2 a \cdot 2 \sqrt{3} a-16 a^{2} \cdot \dfrac{\pi}{6}] \\ & =\dfrac{16 \sqrt{3}}{3} a^{2}+8 \pi a^{2}-4 \sqrt{3} a^{2}-\dfrac{8}{3} \pi a^{2} \\ & =(\dfrac{16 \sqrt{3}}{3}-4 \sqrt{3}) a^{2}+\dfrac{16}{3} \pi a^{2}=\dfrac{4 \sqrt{3}}{3} a^{2}+\dfrac{16}{3} \pi a^{2} \\ & =\dfrac{4}{3}(\sqrt{3}+4 \pi) a^{2} \end{aligned} $

Hence, required area $=\dfrac{4}{3}(\sqrt{3}+4 \pi) a^{2}$ sq. units.

Solution

Given that:

$x+2 y=2 \qquad…(i)$

$ y-x=1 \qquad…(ii) $

$\text{ and } \qquad 2 x+y=7 \qquad…(iii)$

$\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 1 & 0 \\ \hline \end{array}$

$\begin{array}{|c|c|c|} \hline x & 0 & -1 \\ \hline y & 1 & 0 \\ \hline \end{array}$

$\begin{array}{|c|c|c|} \hline x & 0 & 7 / 2 \\ \hline y & 7 & 0 \\ \hline \end{array}$

Solving eqns. (ii) and (iii) we get

$y =1+x$

$\therefore 2 x+1+x =7$

$3 x =6$

$\Rightarrow x =2$

$\therefore y =1+2$

$=3$

Coordinates of $B=(2,3)$

Solving eqns. (i) and (iii) we get

$x +2 y =2$

$\therefore x =2-2 y$

$2 x+y =7$

$ 2(2-2 y)+y =7$

$\Rightarrow 4-4 y+y =7 \Rightarrow-3 y=3$

$\therefore y =-1 \text{ and } x=4$

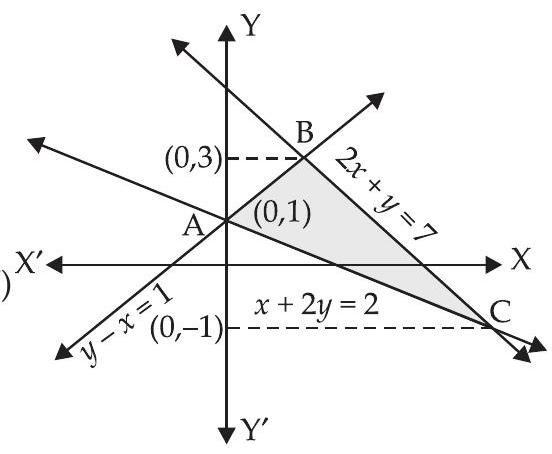
$\therefore$ Coordinates of $C=(4,-1)$ and coordinates of $A=(0,1)$.

Taking the limits on y-axis, we get

$ \begin{matrix} \int _{-1}^{3} x _{BC} d y-\int _{-1}^{1} x _{AC} d y-\int_1^{3} x _{AB} d y \\ =\int _{-1}^{3} \dfrac{7-y}{2} d y-\int _{-1}^{1}(2-2 y) d y-\int_1^{3}(y-1) d y \\ =\dfrac{1}{2}[7 y-\dfrac{y^{2}}{2}] _{-1}^{3}-2[y-\dfrac{y^{2}}{2}] _{-1}^{1}-[\dfrac{y^{2}}{2}-y]_1^{3} \\ =\dfrac{1}{2}[(21-\dfrac{9}{2})-(-7-\dfrac{1}{2})]-2[(1-\dfrac{1}{2})-(-1-\dfrac{1}{2})] -[(\dfrac{9}{2}-3)-(\dfrac{1}{2}-1)] \\ =\dfrac{1}{2} \times 24-2 \times 2-2 \Rightarrow 12-4-2=6 \text{ sq.units } \end{matrix} $

Hence, the required area $=6$ sq. units.

Solution

Given that

and

$ \begin{aligned} & y =4 x+5 \qquad…(i)\\ & y =5-x \qquad…(ii)\\ & 4 y =x+5 \qquad…(iii) \end{aligned} $

$\begin{array}{|c|c|c|} \hline x & 0 & -5 / 4 \\ \hline y & 5 & 0 \\ \hline \end{array}$

$\begin{array}{|c|c|c|} \hline x & 0 & 5 \\ \hline y & 5 & 0 \\ \hline \end{array}$

$\begin{array}{|c|c|c|} \hline x & 0 & -5 \\ \hline y & 5 /4 & 0 \\ \hline \end{array}$

Solving eq. (i) and (ii) we get

$ \begin{matrix} 4 x+5 =5-x \\ \Rightarrow x =0 \text{ and } y=5 \end{matrix} $

$\therefore$ Coordinates of $A=(0,5)$

Solving eq. (ii) and (iii)

$ \begin{aligned} y & =5-x \\ 4 y & =x+5 \\ 5 y & =10 \end{aligned} $

$\therefore y=2$ and $x=3$

$\therefore$ Coordinates of $B=(3,2)$

Solving eq. (i) and (iii)

$ y=4 x+5 $

$ \begin{aligned} & 4 y=x+5 \\ & \Rightarrow \quad 4(4 x+5)=x+5 \\ & \Rightarrow \quad 16 x+20=x+5 \Rightarrow 15 x=-15 \\ & \therefore \quad x=-1 \text{ and } y=1 \end{aligned} $

$\therefore$ Coordinates of $C=(-1,1)$.

$\therefore$ Area of required regions

$=\int _{-1}^{0} y _{AC} d x+\int_0^{3} y _{AB} d x-\int _{-1}^{3} y _{CB} d x$

$=\int _{-1}^{0}(4 x+5) d x+\int_0^{3}(5-x) d x-\int _{-1}^{3} \dfrac{x+5}{4} d x$

$=[4 \dfrac{x^{2}}{2}+5 x] _{-1}^{0}+[5 x-\dfrac{x^{2}}{2}]_0^{3}-\dfrac{1}{4}[\dfrac{x^{2}}{2}+5 x] _{-1}^{3}$

$=[(0+0)-(2-5)]+[(15-\dfrac{9}{2})-(0-0)]-\dfrac{1}{4}[(\dfrac{9}{2}+15)-(\dfrac{1}{2}-5)]$

$=3+\dfrac{21}{2}-\dfrac{1}{4}[\dfrac{39}{2}+\dfrac{9}{2}]=3+\dfrac{21}{2}-\dfrac{1}{4} \times 24 \Rightarrow 3+\dfrac{21}{2}-6$

$=\dfrac{15}{2}$ sq. units

Hence, the required area $=\dfrac{15}{2}$ sq. units.

Solution

Given equation of the curve is $y=2 \cos x$

$\therefore$ Area of the shaded region

$ \int_0^{2 \pi} 2 \cos x d x=\int_0^{\pi / 2} 2 \cos x d x+\int _{\pi / 2}^{3 \pi / 2}|2 \cos x| d x+\int _{3 \pi / 2}^{2 \pi} 2 \cos x d x $

$ \begin{aligned} & =2[\sin x]_0^{\pi / 2}+|[2 \sin x] _{\pi / 2}^{3 \pi / 2}|+2[\sin x] _{3 \pi / 2}^{2 \pi} \\ & =2[\sin \dfrac{\pi}{2}-\sin 0]+|2(\sin \dfrac{3 \pi}{2}-\sin \dfrac{\pi}{2})| \\ & +2[\sin 2 \pi-\sin \dfrac{3 \pi}{2}] \\ & =2(1)+|2(-1-1)|+2(0+1)=2+4+2=8 \text{ sq. units } \end{aligned} $

Solution

Given equations are

$y=1+|x+1|, x=-3$

and $x=3, y=0$

Taking $y=1+|x+1|$

$\Rightarrow \quad y=1+x+1$

$\Rightarrow \quad y=x+2$

and $y=1-x-1 \Rightarrow y=-x$

On solving we get $x=-1$

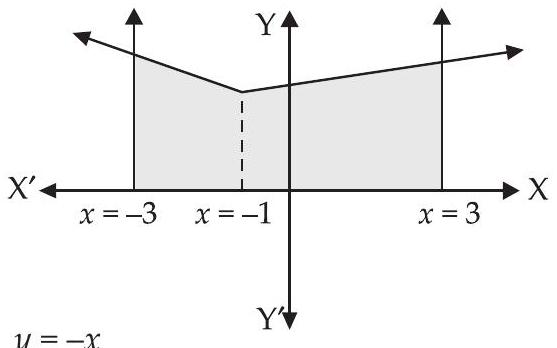
Area of the required regions

$ \begin{aligned} & =\int _{-3}^{-1}-x d x+\int _{-1}^{3}(x+2) d x \\ & =-[\dfrac{x^{2}}{2}] _{-3}^{-1}+[\dfrac{x^{2}}{2}+2 x] _{-1}^{3}=-[\dfrac{1}{2}-\dfrac{9}{2}]+[(\dfrac{9}{2}+6)-(\dfrac{1}{2}-2)] \\ & =-(-4)+[\dfrac{21}{2}+\dfrac{3}{2}]=4+12=16 \text{ sq. units } \end{aligned} $

Hence, the required area $=16$ sq. units.

Solution

Given that $y$-axis, $y=\cos x, y=\sin x, 0 \leq x \leq \dfrac{\pi}{2}$

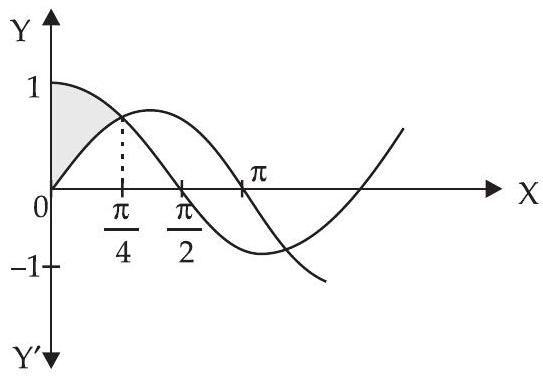
$ \begin{aligned} \text{ Required area } & =\int_0^{\pi / 4} \cos x d x-\int_0^{\pi / 4} \sin x d x \\ & =[\sin x]_0^{\pi / 4}-[-\cos x]_0^{\pi / 4} \\ & =[\sin \dfrac{\pi}{4}-\sin 0]+[\cos \dfrac{\pi}{4}-\cos 0] \\ & =[\dfrac{1}{\sqrt{2}}-0+\dfrac{1}{\sqrt{2}}-1]=\dfrac{2}{\sqrt{2}}-1 \\ & =(\sqrt{2}-1) \text{ sq. units } \end{aligned} $

Hence, the correct option is (c).

• Option (a) $\sqrt{2}$ sq. units: This option is incorrect because the calculated area is $\sqrt{2} - 1$ sq. units, not $\sqrt{2}$ sq. units. The subtraction of 1 is essential in the final result.

• Option (b) $(\sqrt{2}+1)$ sq. units: This option is incorrect because the calculated area is $\sqrt{2} - 1$ sq. units, not $\sqrt{2} + 1$ sq. units. The addition of 1 is not part of the correct area calculation.

• Option (d) $(2 \sqrt{2}-1)$ sq. units: This option is incorrect because the calculated area is $\sqrt{2} - 1$ sq. units, not $2 \sqrt{2} - 1$ sq. units. The factor of 2 in front of $\sqrt{2}$ is not part of the correct area calculation.

Solution

Given that: The equation of parabola is

$ x^{2}=4 y \qquad…(i)$

and equation of straight line is

$x=4 y-2 \qquad…(ii)$

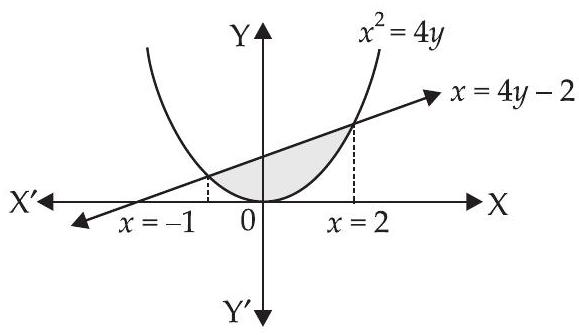
Solving eqn. (i) and (ii) we get

$ y=\dfrac{x^{2}}{4} $

$ \begin{aligned} & x=4(\dfrac{x^{2}}{4})-2 \\ & \Rightarrow \quad x=x^{2}-2 \\ & \Rightarrow \quad x^{2}-x-2=0 \Rightarrow x^{2}-2 x+x-2=0 \\ & \Rightarrow x(x-2)+1(x-2)=0 \Rightarrow(x-2)(x+1)=0 \therefore x=-1, x=2 \\ & \text{ Required area }=\int _{-1}^{2} \dfrac{x+2}{4} d x-\int _{-1}^{2} \dfrac{x^{2}}{4} d x \\ & =\dfrac{1}{4}[\dfrac{x^{2}}{2}+2 x] _{-1}^{2}-\dfrac{1}{4} \cdot \dfrac{1}{3}[x^{3}] _{-1}^{2} \\ & =\dfrac{1}{4}[(\dfrac{4}{2}+4)-(\dfrac{1}{2}-2)]-\dfrac{1}{12}[8+1] \\ & =\dfrac{1}{4}[6+\dfrac{3}{2}]-\dfrac{1}{12}[9]=\dfrac{1}{4} \times \dfrac{15}{2}-\dfrac{3}{4} \\ & =\dfrac{15}{8}-\dfrac{3}{4}=\dfrac{9}{8} \text{ sq. units } \end{aligned} $

Hence, the correct option is $(d)$.

• Option (a) $\dfrac{3}{8}$ sq. units: This option is incorrect because the calculated area of the region bounded by the curve and the straight line is $\dfrac{9}{8}$ sq. units, which is significantly larger than $\dfrac{3}{8}$ sq. units. The integration and algebraic steps show that the area is not as small as $\dfrac{3}{8}$ sq. units.

• Option (b) $\dfrac{5}{8}$ sq. units: This option is incorrect because the calculated area of the region bounded by the curve and the straight line is $\dfrac{9}{8}$ sq. units. The detailed integration process and algebraic simplification confirm that the area is larger than $\dfrac{5}{8}$ sq. units.

• Option (c) $\dfrac{7}{8}$ sq. units: This option is incorrect because the calculated area of the region bounded by the curve and the straight line is $\dfrac{9}{8}$ sq. units. The integration and algebraic steps clearly show that the area is slightly larger than $\dfrac{7}{8}$ sq. units.

Solution

Here, equation of curve is $y=\sqrt{16-x^{2}}$

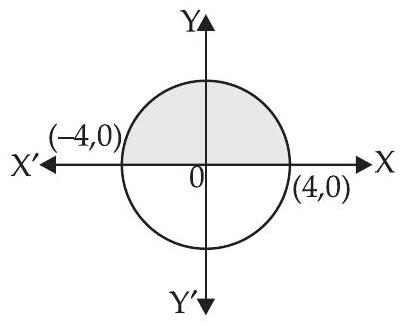
Required area

$ \begin{aligned} & =2[\int_0^{4} \sqrt{16-x^{2}} d x] \\ & =2[\dfrac{x}{2} \sqrt{16-x^{2}}+\dfrac{16}{2} \sin ^{-1} \dfrac{x}{4}]_0^{4} \\ & =2[(0+8 \sin ^{-1} \dfrac{4}{4})-(0+0)] \\ & =2[8 \sin ^{-1}(1)]=16 \cdot \dfrac{\pi}{2}=8 \pi \text{ sq. units } \end{aligned} $

Hence, the correct option is $(a)$.

• Option (b) $20 \pi$ sq. units is incorrect because the integral calculation and the geometric interpretation of the area under the curve $y=\sqrt{16-x^{2}}$ yield an area of $8 \pi$ sq. units, not $20 \pi$ sq. units.

• Option (c) $16 \pi$ sq. units is incorrect because the integral calculation and the geometric interpretation of the area under the curve $y=\sqrt{16-x^{2}}$ yield an area of $8 \pi$ sq. units, not $16 \pi$ sq. units.

• Option (d) $256 \pi$ sq. units is incorrect because the integral calculation and the geometric interpretation of the area under the curve $y=\sqrt{16-x^{2}}$ yield an area of $8 \pi$ sq. units, not $256 \pi$ sq. units.

Solution

Given equation of circle is $x^{2}+y^{2}=32 \Rightarrow x^{2}+y^{2}=(4 \sqrt{2})^{2}$ and the line is $y=x$ and the $x$-axis.

Solving the two equations we have

$x^{2}+x^{2} =32$

$\Rightarrow 2 x^{2} =32$

$\Rightarrow x^{2} =16$

$\therefore x = \pm 4$

Required area

$ \begin{aligned} & =\int_0^{4} x d x+\int_4^{4 \sqrt{2}} \sqrt{(4 \sqrt{2})^{2}-x^{2}} d x \\ & =\dfrac{1}{2}[x^{2}]_0^{4}+[\dfrac{x}{2} \sqrt{(4 \sqrt{2})^{2}-x^{2}}+\dfrac{32}{2} \sin ^{-1} \dfrac{x}{4 \sqrt{2}}]_4^{4 \sqrt{2}} \\ & =\dfrac{1}{2}[16-0]+[0+16 \sin ^{-1}(\dfrac{4 \sqrt{2}}{4 \sqrt{2}})-2 \sqrt{32-16}-16 \sin ^{-1} \dfrac{4}{4 \sqrt{2}}] \\ & =8+[16 \sin ^{-1}(1)-8-16 \sin ^{-1} \dfrac{1}{\sqrt{2}}] \\ & =8+16 \cdot \dfrac{\pi}{2}-8-16 \cdot \dfrac{\pi}{4}=8 \pi-4 \pi=4 \pi \text{ sq. units } \end{aligned} $

Hence, the correct option is $(b)$.

• Option (a) $16 \pi$ sq. units: This option is incorrect because it overestimates the area. The actual area calculation involves integrating the region bounded by the line $y=x$ and the circle $x^2 + y^2 = 32$, which results in a smaller area of $4 \pi$ sq. units.

• Option (c) $32 \pi$ sq. units: This option is incorrect because it significantly overestimates the area. The total area of the circle itself is $32 \pi$ sq. units, but the region in question is only a small part of the circle, specifically in the first quadrant and bounded by the line $y=x$ and the $x$-axis.

• Option (d) 24 sq. units: This option is incorrect because it does not account for the circular segment’s area correctly. The area calculation involves both the triangular region under the line $y=x$ and the segment of the circle, which results in an area of $4 \pi$ sq. units, not 24 sq. units.

Solution

Given that: $y=\cos x, x=0, x=\pi$

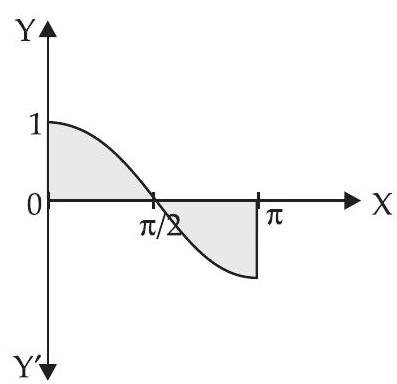
Required area

$ \begin{aligned} & =\int_0^{\pi / 2} \cos x d x+|\int _{\pi / 2}^{\pi} \cos x d x| \\ & =[\sin x]_0^{\pi / 2}+|(\sin x) _{\pi / 2}^{\pi}| \\ & =[\sin \dfrac{\pi}{2}-\sin 0]+|[\sin \pi-\sin \dfrac{\pi}{2}]| \\ & =(1-0)+|0-1|=1+1=2 \text{ sq. units } \end{aligned} $

Hence, the correct option is $(a)$.

• Option (b) 4 sq. units: This option is incorrect because the integral of the cosine function from $x = 0$ to $x = \pi$ results in an area of 2 square units, not 4. The calculation shows that the total area under the curve $y = \cos x$ between these limits is 2 square units.

• Option (c) 3 sq. units: This option is incorrect because the integral of the cosine function from $x = 0$ to $x = \pi$ results in an area of 2 square units, not 3. The calculation confirms that the total area under the curve $y = \cos x$ between these limits is 2 square units.

• Option (d) 1 sq. unit: This option is incorrect because the integral of the cosine function from $x = 0$ to $x = \pi$ results in an area of 2 square units, not 1. The calculation demonstrates that the total area under the curve $y = \cos x$ between these limits is 2 square units.

Solution

Given equation of parabola is $y^{2}=x$ and equation of straight line is $2 y=x$

Solving eqns. (i) and (ii) we get

$ \begin{aligned} & (\dfrac{x}{2})^{2}=x \Rightarrow \dfrac{x^{2}}{4}=x \Rightarrow x^{2}=4 x \\ & \Rightarrow x(x-4)=0\\ & \therefore x=0,4 \end{aligned} $

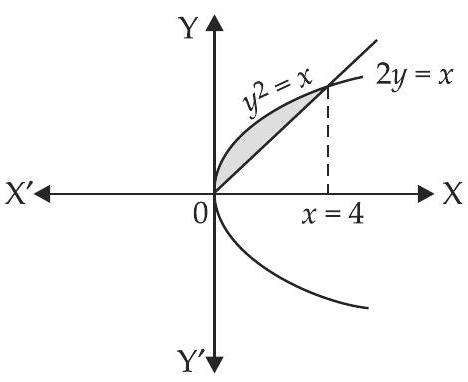
Required area

$ \begin{aligned} & =\int_0^{4} \sqrt{x} d x-\int_0^{4} \dfrac{x}{2} d x \\ & =\dfrac{2}{3}[x^{3 / 2}]_0^{4}-\dfrac{1}{2} \cdot \dfrac{1}{2}[x^{2}]_0^{4} \end{aligned} $

$=\dfrac{2}{3}[(4)^{3 / 2}-0]-\dfrac{1}{4}[(4)^{2}-0]=\dfrac{2}{3} \times 8-\dfrac{1}{4} \times 16$

$=\dfrac{16}{3}-4=\dfrac{4}{3}$ sq. units

Hence, the correct answer is $(a)$.

• Option (b) 1 sq. unit: This option is incorrect because the calculated area of the region bounded by the parabola $ y^2 = x $ and the line $ 2y = x $ is $\dfrac{4}{3}$ sq. units, not 1 sq. unit. The integration and subtraction of the areas under the curves do not result in 1 sq. unit.

• Option (c) $\dfrac{2}{3}$ sq. units: This option is incorrect because the area calculation involves integrating the functions $\sqrt{x}$ and $\dfrac{x}{2}$ over the interval from 0 to 4. The correct result of this integration and subtraction is $\dfrac{4}{3}$ sq. units, not $\dfrac{2}{3}$ sq. units.

• Option (d) $\dfrac{1}{3}$ sq. units: This option is incorrect because the area derived from the integration process is $\dfrac{4}{3}$ sq. units. The value $\dfrac{1}{3}$ sq. units does not match the result of the correct mathematical operations performed to find the area between the given curves.

Solution

Given equation of curve is $y=\sin x$ between $x=0$ and $x=\dfrac{\pi}{2}$

Area of required region

$ \begin{aligned} & =\int_0^{\pi / 2} \sin x d x=-[\cos x]_0^{\pi / 2} \\ & =-[\cos \dfrac{\pi}{2}-\cos 0] \\ & =-[0-1]=1 \text{ sq. unit } \end{aligned} $

• Option (a) is incorrect because the integral of $\sin x$ from $0$ to $\dfrac{\pi}{2}$ does not yield 2 sq. units. The correct integral calculation results in 1 sq. unit.
• Option (b) is incorrect because the integral of $\sin x$ from $0$ to $\dfrac{\pi}{2}$ does not yield 4 sq. units. The correct integral calculation results in 1 sq. unit.
• Option (c) is incorrect because the integral of $\sin x$ from $0$ to $\dfrac{\pi}{2}$ does not yield 3 sq. units. The correct integral calculation results in 1 sq. unit.

Solution

Given equation of ellipse is $\dfrac{x^{2}}{25}+\dfrac{y^{2}}{16}=1$

$\Rightarrow \dfrac{y^{2}}{16}=1-\dfrac{x^{2}}{25} \Rightarrow y^{2}=\dfrac{16}{25}(25-x^{2})$

$\therefore \quad y=\dfrac{4}{5} \sqrt{25-x^{2}}$

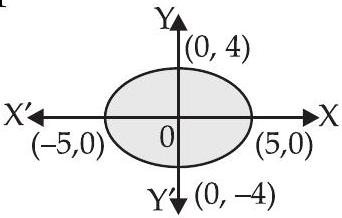
$\therefore$ Since the ellipse is symmetrical about the axes.

$\therefore$ Required area $=4 \times \int_0^{5} \dfrac{4}{5} \sqrt{25-x^{2}} d x=4 \times \dfrac{4}{5} \int_0^{5} \sqrt{(5)^{2}-x^{2}} d x$

$ \begin{aligned} & =\dfrac{16}{5}[\dfrac{x}{2} \sqrt{(5)^{2}-x^{2}}+\dfrac{25}{2} \sin ^{-1} \dfrac{x}{5}]_0^{5} \\ & =\dfrac{16}{5}[0+\dfrac{25}{2} \cdot \sin ^{-1}(\dfrac{5}{5})-0-0]=\dfrac{16}{5}[\dfrac{25}{2} \cdot \sin ^{-1}(1)] \\ & =\dfrac{16}{5}[\dfrac{25}{2} \cdot \dfrac{\pi}{2}]=20 \pi \text{ sq. units } \end{aligned} $

Hence, the correct answer is (a).

• Option (b) $20 \pi^{2}$ sq. units: This option is incorrect because the area of an ellipse is given by the formula $\pi \times a \times b$, where $a$ and $b$ are the semi-major and semi-minor axes, respectively. The correct calculation yields $20 \pi$ sq. units, not $20 \pi^{2}$ sq. units. The presence of $\pi^2$ is a mathematical error.

• Option (c) $16 \pi^{2}$ sq. units: This option is incorrect for similar reasons as option (b). The area of the ellipse should be calculated using the formula $\pi \times a \times b$. The correct area is $20 \pi$ sq. units, and the inclusion of $\pi^2$ and the incorrect numerical factor of 16 instead of 20 makes this option incorrect.

• Option (d) $25 \pi$ sq. units: This option is incorrect because it miscalculates the area of the ellipse. The correct area is $20 \pi$ sq. units, derived from the semi-major axis $a = 5$ and the semi-minor axis $b = 4$. The factor of 25 is incorrect and does not align with the correct formula for the area of an ellipse.

Solution

Given equation of circle is

$x^{2}+y^{2}=1 \Rightarrow y=\sqrt{1-x^{2}}$

Since the circle is symmetrical about the axes.

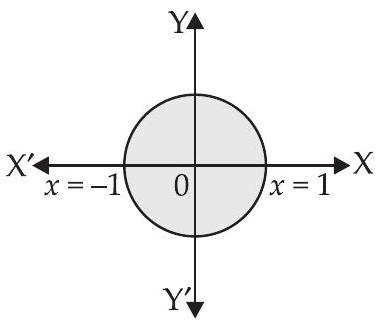
$\therefore$ Required area $=4 \times \int_0^{1} \sqrt{1-x^{2}} d x$

$=4[\dfrac{x}{2} \sqrt{1-x^{2}}+\dfrac{1}{2} \sin ^{-1} x]_0^{1}$

$=4[0+\dfrac{1}{2} \sin ^{-1}(1)-0-0]$

$=4 \times \dfrac{1}{2} \times \dfrac{\pi}{2}=\pi$ sq. units

Hence, the correct answer is $(b)$.

• Option (a) $2 \pi$ sq. units is incorrect because the area of a circle with radius 1 is given by the formula $\pi r^2$. For a circle with radius 1, the area is $\pi \times 1^2 = \pi$ sq. units, not $2 \pi$ sq. units.

• Option (c) $3 \pi$ sq. units is incorrect because, as mentioned, the area of a circle with radius 1 is $\pi$ sq. units. There is no mathematical basis for the area being $3 \pi$ sq. units.

• Option (d) $4 \pi$ sq. units is incorrect because the area of a circle with radius 1 is $\pi$ sq. units. The value $4 \pi$ sq. units would correspond to a circle with a radius of 2, not 1.

Solution

Given equation of lines are

$y=x+1, x=2 \text{ and } x=3$

Required area

$ \begin{aligned} & =\int_2^{3}(x+1) d x=[\dfrac{x^{2}}{2}+x]_2^{3} \\ & =(\dfrac{9}{2}+3)-(\dfrac{4}{2}+2) \\ & =\dfrac{15}{2}-4=\dfrac{7}{2} \text{ sq.units } \end{aligned} $

Hence, the correct option is (a).

• Option (b) $\dfrac{9}{2}$ sq. units is incorrect because the integral calculation of the area between $x=2$ and $x=3$ for the function $y=x+1$ results in $\dfrac{7}{2}$ sq. units, not $\dfrac{9}{2}$ sq. units.

• Option (c) $\dfrac{11}{2}$ sq. units is incorrect because the integral calculation of the area between $x=2$ and $x=3$ for the function $y=x+1$ results in $\dfrac{7}{2}$ sq. units, not $\dfrac{11}{2}$ sq. units.

• Option (d) $\dfrac{13}{2}$ sq. units is incorrect because the integral calculation of the area between $x=2$ and $x=3$ for the function $y=x+1$ results in $\dfrac{7}{2}$ sq. units, not $\dfrac{13}{2}$ sq. units.

Solution

Given equations of lines are $x=2 y+3, y=1$ and $y=-1$

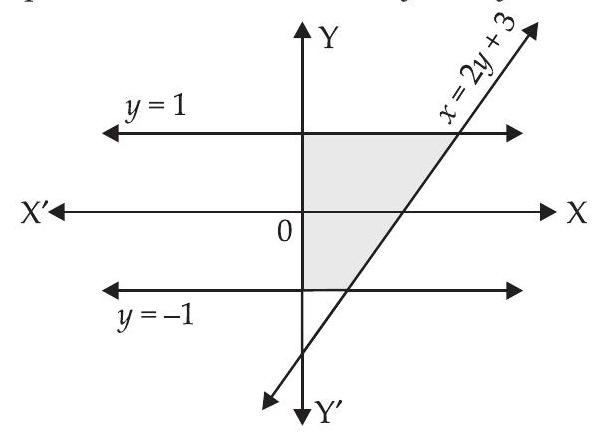
$ \begin{aligned} \text{ Required area } & =\int _{-1}^{1}(2 y+3) d y \\ & =2 \cdot \dfrac{1}{2}[y^{2}] _{-1}^{1}+3[y] _{-1}^{1} \\ & =(1-1)+3(1+1)=6 \text{ sq. units } \end{aligned} $

Hence, the correct answer is (c).

• Option (a) 4 sq. units: This option is incorrect because the integral calculation of the area between the given curve and the lines $ y = 1 $ and $ y = -1 $ results in 6 sq. units, not 4 sq. units. The integral $\int_{-1}^{1} (2y + 3) , dy$ evaluates to 6, as shown in the solution.

• Option (b) $\dfrac{3}{2}$ sq. units: This option is incorrect because the integral calculation of the area between the given curve and the lines $ y = 1 $ and $ y = -1 $ results in 6 sq. units, not $\dfrac{3}{2}$ sq. units. The integral $\int_{-1}^{1} (2y + 3) , dy$ evaluates to 6, as shown in the solution.

• Option (d) 8 sq. units: This option is incorrect because the integral calculation of the area between the given curve and the lines $ y = 1 $ and $ y = -1 $ results in 6 sq. units, not 8 sq. units. The integral $\int_{-1}^{1} (2y + 3) , dy$ evaluates to 6, as shown in the solution.