Differential Equations
Short Answer Type Questions
1. Find the solution of $\frac{d y}{d x}=2^{y-x}$.
Show Answer
Solution
The given differential equation is
Separating the variables, we get
$ \frac{d y}{d x}=2^{y-x} \Rightarrow \frac{d y}{d x}=\frac{2^{y}}{2^{x}} $
$ \frac{d y}{2^{y}}=\frac{d x}{2^{x}} \Rightarrow 2^{-y} d y=2^{-x} d x $
Integrating both sides, we get
$ \begin{aligned} \int 2^{-y} d y & =\int 2^{-x} d x \\ & \\ \frac{-2^{-y}}{\log 2} & =\frac{-2^{-x}}{\log 2}+c \quad \Rightarrow-2^{-y}=-2^{-x}+c \log 2 \\ \Rightarrow \quad-2^{-y}+2^{-x} & =c \log 2 \\ \Rightarrow \quad 2^{-x}-2^{-y} & =k \quad \quad \quad \text where \quad c \log 2=k \end{aligned} $
2. Find the differential equation of all non vertical lines in a plane.
Show Answer
Solution
Equation of all non vertical lines are $y=m x+c$
Differentiating with respect to $x$, we get $\frac{d y}{d x}=m$
Again differentiating w.r.t. $x$ we have $\frac{d^{2} y}{d x^{2}}=0$
Hence, the required equation is $\frac{d^{2} y}{d x^{2}}=0$.
3. Given that $\frac{d y}{d x}=e^{-2 y}$ and $y=0$ when $x=5$. Find the value of $x$ when $y=3$.
Show Answer
Solution
Given equation is
$ \begin{aligned} & \frac{d y}{d x} & =e^{-2 y} \end{aligned} $
Separating the variables, we get
$ \begin{aligned} \Rightarrow \quad \frac{d y}{e^{-2 y}} & =d x \Rightarrow e^{2 y} \cdot d y=d x \end{aligned} $
Integrating both sides, we get
$ \int e^{2 y} d y=\int d x \Rightarrow \frac{1}{2} e^{2 y}=x+c $
Put $y=0$ and $x=5$ (Given)
$\Rightarrow \frac{1}{2} e^{0}=5+c \Rightarrow c=\frac{1}{2}-5=-\frac{9}{2}$
$\therefore$ The equation becomes $\frac{1}{2} e^{2 y}=x-\frac{9}{2}$
Now putting $y=3$, we get
$ \frac{1}{2} e^{6}=x-\frac{9}{2} \Rightarrow x=\frac{1}{2} e^{6}+\frac{9}{2} $
Hence the required value of $x=\frac{1}{2}(e^{6}+9)$.
4. Solve the differential equation $(x^{2}-1) \frac{d y}{d x}+2 x y=\frac{1}{x^{2}-1}$.
Show Answer
Solution
Given differential equation is
$ (x^{2}-1) \frac{d y}{d x}+2 x y=\frac{1}{x^{2}-1} $
Dividing by $(x^{2}-1)$, we get
$ \frac{d y}{d x}+\frac{2x y}{x^{2}-1}=\frac{1}{(x^{2}-1)^{2}} $
It is a linear differential equation of first order and first degree.
Here, $ P=\frac{2 x}{x^{2}-1}$ and $Q=\frac{1}{(x^{2}-1)^{2}}$
Integrating factor I.F. $=e^{\int P d x}=e^{\int \frac{2 x}{x^{2}-1} d x}=e^{\log |(x^{2}-1)|}=(x^{2}-1) , ((x^{2}-1)>0)$
$\therefore$ Solution of the equation is
$ \begin{aligned} & y \times \text{ I.F. }=\int Q \times \text{ I.F. } d x+\text{ C } \\ & \Rightarrow y \times(x^{2}-1)=\int \frac{1}{(x^{2}-1)^{2}} \times(x^{2}-1) d x+\text{ C } \\ & \Rightarrow y(x^{2}-1)=\int \frac{1}{x^{2}-1} d x+C \end{aligned} $
$ \Rightarrow y(x^{2}-1)=\frac{1}{2} \log (|\frac{x-1}{x+1}|)+C$
Hence the required solution is $y(x^{2}-1)=\frac{1}{2} \log (|\frac{x-1}{x+1}|)+C$.
5. Solve the differential equation $\frac{d y}{d x}+2 x y=y$.
Show Answer
Solution
Given equation is $\frac{d y}{d x}+2 x y=y$.
$ \Rightarrow \quad \frac{d y}{d x}=y-2 x y \quad \Rightarrow \frac{d y}{d x}=y(1-2 x) \\ \Rightarrow \frac{d y}{y}=(1-2 x) d x $
Integrating both sides, we have
$ \begin{aligned} & \int \frac{d y}{ y}=\int(1-2 x) d x \Rightarrow \log |y|=x-2 \cdot \frac{x^{2}}{2}+\log |c| \\ & \Rightarrow \quad \log |y|=x-x^{2}+\log |c| \Rightarrow \log |y|-\log |c|=x-x^{2} \\ & \Rightarrow \quad \log |\frac{y}{c}|=x-x^{2} \Rightarrow |{y}|=|{c}|e^{x-x^{2}} \\ \Rightarrow {y}=\pm {c}e^{x-x^{2}} \\ & \therefore \quad y=C \cdot e^{x-x^{2}} (where \quad C=\pm c) \end{aligned} $
Hence, the required solution is $y=C \cdot e^{x-x^{2}}$.
6. Find the general solution of $\frac{d y}{d x}+a y=e^{m x}$.
Show Answer
Solution
Given equation is $\frac{d y}{d x}+a y=e^{m x}$.
Here, $P=a$ and $Q=e^{m x}$
$\therefore$ I.F. $=e^{\int P d x}=e^{\int a \cdot d x}=e^{a x}$.
Solution of equation is $y \times$ I.F $=\int Q \times $ I.F. $d x+c$
$ \begin{matrix} \Rightarrow \quad y \cdot e^{a x}=\int e^{m x} \cdot e^{a x} d x+c \Rightarrow y \cdot e^{a x}=\int e^{(m+a) x} d x+c \\ \Rightarrow \qquad y \cdot e^{a x}=\frac{e^{(m+a) x}}{(m+a)}+c \Rightarrow y=\frac{e^{(m+a) x}}{(m+a)} \cdot e^{-a x}+c \cdot e^{-a x} \\ \therefore \qquad y=\frac{e^{m x}}{(m+a)}+c \cdot e^{-a x} \end{matrix} $
$ \Rightarrow (m+a)y = e^{mx}+ c(m+a)e^{-ax}$
$ \Rightarrow (m+a)y = e^{mx}+ Ce^{-ax} (where \quad C= c(m+a))$
Hence the required solution is $ (m+a)y = e^{mx}+ Ce^{-ax}$
7. Solve the differential equation $\frac{d y}{d x}+1=e^{x+y}$.
Show Answer
Solution
Given that: $\frac{d y}{d x}+1=e^{x+y}$
Put $x+y=t$
Differentiate both sides w.r.t. x , (we get)
$ \begin{matrix} \therefore & 1+\frac{d y}{d x} & =\frac{d t}{d x} \\ \therefore & \frac{d t}{d x} & =e^{t} \Rightarrow \frac{d t}{e^{t}}=d x \\ \Rightarrow e^{-t} d t=d x \end{matrix} $
Integrating both sides, we have
$ \begin{gathered} \int e^{-t} d t=\int d x \Rightarrow-e^{-t}=x+c \\ \Rightarrow \quad-e^{-(x+y)}=x+c \Rightarrow \frac{-1}{e^{x+y}}=x+c \Rightarrow(x+c) e^{x+y}=-1 \end{gathered} $
Hence, the required solution is $(x+c) \ e^{x+y} \ +1=0$.
8. Solve: $y d x-x d y=x^{2} y d x$.
Show Answer
Solution
Given equation is $y d x-x d y=x^{2} y d x$.
$ \begin{aligned} & \Rightarrow \quad y d x-x^{2} y d x=x d y \\ & \Rightarrow \quad y(1-x^{2}) d x=x d y \\ & \Rightarrow \quad(\frac{1-x^{2}}{x}) d x=\frac{d y}{y} \Rightarrow(\frac{1}{x}-x) d x=\frac{d y}{y} \end{aligned} $
Integrating both sides we get
$ \begin{aligned} & \int(\frac{1}{x}-x) d x=\int \frac{d y}{y} \\ \Rightarrow & \log |x|-\frac{x^{2}}{2}=\log |y|+\log |c| \end{aligned} $
$ \begin{aligned} & \Rightarrow \log |x|-\frac{x^{2}}{2}=\log |y c| \Rightarrow \log |x|-\log |y c|=\frac{x^{2}}{2} \\ & \Rightarrow \log |\frac{x}{y c}|=\frac{x^{2}}{2} \Rightarrow |\frac{x}{y c}|=e^\frac{x^{2}}{2} \\ & \Rightarrow \quad \frac{x}{y c}=\pm e^{x^{2} / 2} \Rightarrow \frac{y c}{x}=\mp e^{-x^{2} / 2} \Rightarrow y c=\mp x e^{-x^{2} / 2} \\ & \therefore \quad y=\mp \frac{1}{c} \cdot x e^{-x^{2} / 2} \Rightarrow y=k x e^{-x^{2} / 2} \quad[where \quad k=\mp \frac{1}{c}] \end{aligned} $
Hence, the required solution is $y=k x e^{-x^{2} / 2}$.
9. Solve the differential equation $\frac{d y}{d x}=1+x+y^{2}+x y^{2}$, when $y=0, x=0$.
Show Answer
Solution
Given equation is
$ \begin{aligned} \frac{d y}{d x} & =1+x+y^{2}+x y^{2} \\ \Rightarrow \quad \frac{d y}{d x} & =1(1+x)+y^{2}(1+x) \\ \Rightarrow \quad \frac{d y}{d x} & =(1+x)(1+y^{2})\\ \Rightarrow \quad \frac{d y}{1+y^{2}}=(1+x) d x \end{aligned} $
Integrating both sides, we get
$ \int \frac{d y}{1+y^{2}}=\int(1+x) d x \Rightarrow \tan ^{-1} y=x+\frac{x^{2}}{2}+c $
Put $x=0$ and $y=0$, we get $\tan ^{-1}(0)=0+0+c \Rightarrow c=0$
$\therefore \quad \tan ^{-1} y=x+\frac{x^{2}}{2} \Rightarrow y=\tan (x+\frac{x^{2}}{2})$
Hence, the required solution is $y=\tan (x+\frac{x^{2}}{2})$.
10. Find the general solution of $(x+2 y^{3}) \frac{d y}{d x}=y$.
Show Answer
Solution
Given equation is $(x+2 y^{3}) \frac{d y}{d x}=y$
$ \begin{aligned} & \Rightarrow \quad \frac{d y}{d x}=\frac{y}{x+2 y^{3}} \Rightarrow \frac{d x}{d y}=\frac{x+2 y^{3}}{y} \\ & \Rightarrow \quad \frac{d x}{d y}=\frac{x}{y}+\frac{2 y^{3}}{y} \Rightarrow \frac{d x}{d y}-\frac{x}{y}=2 y^{2} \end{aligned} $
It is a linear differential equation of first order and first degree.
Here $P=-\frac{1}{y}$ and $Q=2 y^{2}$.
$\therefore$ Integrating factor I.F. $=e^{\int P d y}=e^{\int-\frac{1}{y} d y}=e^{-\log |y|}=e^{\log \frac{1}{|y|}}=\frac{1}{|y|}, \quad (y \neq 0)$
For $ y > 0 $
So the solution of the equation is
$ \begin{aligned} x \times I . F . & =\int Q \times \text{ I.F. } d y+c \\ x \cdot \frac{1}{y} & =\int 2 y^{2} \cdot \frac{1}{y} d y+c \\ \Rightarrow \quad \frac{x}{y} & =2 \int y d y+c \Rightarrow \frac{x}{y}=2 \cdot \frac{y^{2}}{2}+c \Rightarrow \frac{x}{y}=y^{2}+c \end{aligned} $
So $x=y(y^{2}+c)$
For $ y < 0 $
So the solution of the equation is
$ \begin{aligned} x \times I . F . & =\int Q \times \text{ I.F. } d y+k \\ x \cdot \frac{1}{-y} & =\int 2 y^{2} \cdot \frac{1}{-y} d y+k \\ \Rightarrow \quad \frac{x}{y} & =2 \int y d y-k \Rightarrow \frac{x}{y}=2 \cdot \frac{y^{2}}{2}-k \Rightarrow \frac{x}{y}=y^{2}-k \end{aligned} $
So $x=y(y^{2}-k)$
Hence, the required solution is $x=y(y^{2}+C)$.
11. If $y(x)$ is a solution of $(\frac{2+\sin x}{1+y}) \frac{d y}{d x}=-\cos x$ and $y(0)=1$, then find the value of $y(\frac{\pi}{2})$.
Show Answer
Solution
Given equation is
$ \begin{aligned} & (\frac{2+\sin x}{1+y}) \frac{d y}{d x}=-\cos x \\ \Rightarrow &(\frac{2+\sin x}{\cos x}) \frac{d y}{d x}=-(1+y)\\ \Rightarrow \frac{d y}{(1+y)}=-(\frac{\cos x}{2+\sin x}) d x \end{aligned} $
Integrating both sides, we get
$ \begin{aligned} \int \frac{d y}{1+y} & =-\int \frac{\cos x}{2+\sin x} d x \\ \log |1+y| & =-\log |2+\sin x|+\log |c| \\ \Rightarrow \log |1+y|+\log |2+\sin x| & =\log |c| \\ \Rightarrow \quad \log |(1+y)(2+\sin x)| & =\log |c| \Rightarrow |(1+y)(2+\sin x)|=|c| \\ \Rightarrow (1+y)(2+\sin x)=\pm c \\ \Rightarrow (1+y)(2+\sin x)= C, \quad (where \quad C =\pm c) \end{aligned} $
Put $x=0$ and $y=1$, we get
$(1+1)(2+\sin 0)=C \Rightarrow 4=C$
$\therefore$ equation is $(1+y)(2+\sin x)=4$
Now put $x=\frac{\pi}{2}$
$ \begin{aligned} & \therefore \quad(1+y)(2+\sin \frac{\pi}{2})=4 \\ & \Rightarrow \quad(1+y)(2+1)=4 \Rightarrow 1+y=\frac{4}{3} \Rightarrow y=\frac{4}{3}-1 \Rightarrow y=\frac{1}{3} \end{aligned} $
So, $y(\frac{\pi}{2})=\frac{1}{3}$
Hence, the required solution is $y(\frac{\pi}{2})=\frac{1}{3}$.
12. If $y(t)$ is a solution of $(1+t) \frac{d y}{d t}-t y=1$ and $y(0)=-1$, then show that $y(1)=-\frac{1}{2}$.
Show Answer
Solution
Given equation is
$ (1+t) \frac{d y}{d t}-t y=1 \Rightarrow \frac{d y}{d t}-(\frac{t}{1+t}) y=\frac{1}{1+t} $
It is a linear differential equation of first order and first degree.
Here, $P=\frac{-t}{1+t}$ and $Q=\frac{1}{1+t}$
$\therefore$ Integrating factor I.F. $=e^{\int P d t}=e^{\int \frac{-t}{1+t} d t}=e^{-\int \frac{1+t-1}{1+t} d t}$
$ \begin{aligned} & I.F. =e^{-\int(1-\frac{1}{1+t}) d t}=e^{-[t-\log |(1+t)|]} \\ & =e^{-t+\log |(1+t)|}=e^{-t} \cdot e^{\log (1+t)} , \quad ((1+t)>0) \end{aligned} $
$\therefore$ I.F. $=e^{-t} \cdot(1+t)$
Required solution of the given differential equation is
$ \begin{matrix} y \times \text{ I.F. } =\int \text Q \times {I.F. } d t+c \\ \Rightarrow \qquad y \cdot e^{-t}(1+t) =\int \frac{1}{(1+t)} \cdot e^{-t} \cdot(1+t) d t+c \\ \Rightarrow \qquad y \cdot e^{-t}(1+t) =\int e^{-t} d t+c \\ \Rightarrow \qquad y \cdot e^{-t}(1+t) =-e^{-t}+c \end{matrix} $
$ \begin{aligned} & \text{ Put } t=0 \text{ and } y=-1 , [\because y(0)=-1] \\ & \Rightarrow \quad-1 \cdot e^{0} \cdot 1=-e^{0}+c \\ & \Rightarrow \quad-1=-1+c \Rightarrow c=0 \end{aligned} $
So the equation becomes
$ y e^{-t}(1+t)=-e^{-t} $
Now put $t=1$
$\therefore \quad y \cdot e^{-1}(1+1)=-e^{-1}$
$\Rightarrow \quad 2 y=-1 \Rightarrow y=-\frac{1}{2}$
Hence $y(1)=-\frac{1}{2}$ is verified.
13. Form the differential equation having $y=(\sin ^{-1} x)^{2}+A$ $\cos ^{-1} x+B$ where $A$ and $B$ are arbitrary constants, as its general solution.
Show Answer
Solution
Given equation is $y=(\sin ^{-1} x)^{2}+A \cos ^{-1} x+B$
$ \frac{d y}{d x}=2 \sin ^{-1} x \cdot \frac{1}{\sqrt{1-x^{2}}}+A \cdot(\frac{-1}{\sqrt{1-x^{2}}}) $
Multiplying both sides by $\sqrt{1-x^{2}}$, we get
$ \sqrt{1-x^{2}} \frac{d y}{d x}=2 \sin ^{-1} x-A $
Again differentiating w.r.t $x$, we get
$ \begin{aligned} & \sqrt{1-x^{2}} \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x} \cdot \frac{1 \times(-2 x)}{2 \sqrt{1-x^{2}}}=\frac{2}{\sqrt{1-x^{2}}} \\ \Rightarrow \quad & \sqrt{1-x^{2}} \frac{d^{2} y}{d x^{2}}-\frac{x}{\sqrt{1-x^{2}}} \frac{d y}{d x}=\frac{2}{\sqrt{1-x^{2}}} \end{aligned} $
Multiplying both sides by $\sqrt{1-x^{2}}$, we get
$ \Rightarrow \quad(1-x^{2}) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}-2=0 $
Which is the required differential equation.
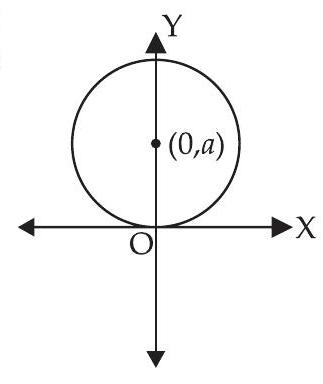
14. Form the differential equation of all circles which pass through origin and whose centres lie on $y$-axis.
Show Answer
Solution
Equation of circle which passes through the origin and whose centre lies on $y$-axis is
$$(x-0)^{2}+(y-a)^{2} =a^{2}$$
$$\Rightarrow \qquad x^{2}+y^{2}+a^{2}-2 a y =a^{2}$$
$$\Rightarrow \qquad x^{2}+y^{2}-2 a y =0 \tag{i}$$
Differentiate w.r.t. x , we get
$\Rightarrow \quad 2 x+2 y \cdot \frac{d y}{d x}-2 a \cdot \frac{d y}{d x}=0$
$\Rightarrow \quad x+y \frac{d y}{d x}-a \cdot \frac{d y}{d x}=0 \Rightarrow x+(y-a) \cdot \frac{d y}{d x}=0$
$ y-a=\frac{-x}{d y / d x} $
$ \therefore \quad a=y+\frac{x}{d y / d x} $
Putting the value of $a$ in eq. (i), we get
$ \begin{aligned} & x^{2}+y^{2}-2(y+\frac{x}{d y / d x}) y=0 \\ & \Rightarrow \quad x^{2}+y^{2}-2 y^{2}-\frac{2 x y}{\frac{d y}{d x}}=0 \Rightarrow x^{2}-y^{2}=\frac{2 x y}{\frac{d y}{d x}} \\ & \therefore \quad(x^{2}-y^{2}) \frac{d y}{d x}-2 x y=0 \end{aligned} $
Hence, the required differential equation is
$ (x^{2}-y^{2}) \frac{d y}{d x}-2 x y=0 $
15. Find the equation of a curve passing through origin and satisfying the differential equation $(1+x^{2}) \frac{d y}{d x}+2 x y=4 x^{2}$.
Show Answer
Solution
Given equation is
$ \begin{aligned} & (1+x^{2}) \frac{d y}{d x}+2 x y=4 x^{2} \\ & \Rightarrow \quad \frac{d y}{d x}+\frac{2 x}{1+x^{2}} \cdot y=\frac{4 x^{2}}{1+x^{2}} \end{aligned} $
It is a linear differential equation of first order and first degree.
Here, $P=\frac{2 x}{1+x^{2}}$ and $Q=\frac{4 x^{2}}{1+x^{2}}$
Integrating factor I.F. $=e^{\int P d x}=e^{\int \frac{2 x}{1+x^{2}} d x}=e^{\log |(1+x^{2})|}=|(1+x^{2})| = (1+ x^{2} ) , \quad (\because \quad (1+ x^{2} ) \quad is \quad positive) $
$\therefore$ Solution is
$$ \begin{align*} & y \times \text{ I.F. }=\int Q \times \text{ I.F. } d x+c \\ & \Rightarrow y(1+x^{2})=\int \frac{4 x^{2}}{1+x^{2}} \times(1+x^{2}) d x+c \\ & \Rightarrow \quad y(1+x^{2})=\int 4 x^{2} d x+c \\ & \Rightarrow \quad y(1+x^{2})=\frac{4}{3} x^{3}+c \tag{i} \end{align*} $$
Since the curve is passing through origin i.e., $(0,0)$
$\therefore$ Put $y=0$ and $x=0$ in eq. (i)
$0(1+0)=\frac{4}{3}(0)^{3}+c \Rightarrow c=0$
$\therefore$ Equation is $y(1+x^{2})=\frac{4}{3} x^{3} \Rightarrow y=\frac{4 x^{3}}{3(1+x^{2})}$
Hence, the required solution is $y=\frac{4 x^{3}}{3(1+x^{2})}$.
16. Solve : $x^{2} \cdot \frac{d y}{d x}=x^{2}+x y+y^{2}$
Show Answer
Solution
Given equation is $x^{2} \frac{d y}{d x}=x^{2}+x y+y^{2}$
$ \Rightarrow \quad \frac{d y}{d x}=\frac{x^{2}+x y+y^{2}}{x^{2}} $ (Homogenious differential equation )
Put $y=v x$
$\therefore \quad \frac{d y}{d x}=v+x \cdot \frac{d v}{d x}$
$\therefore \quad v+x \cdot \frac{d v}{d x}=\frac{x^{2}+v x^{2}+v^{2} x^{2}}{x^{2}}$
$\Rightarrow \quad v+x \cdot \frac{d v}{d x}=\frac{x^{2}(1+v+v^{2})}{x^{2}}$
$\Rightarrow \quad v+x \cdot \frac{d v}{d x}=1+v+v^{2} \Rightarrow x \cdot \frac{d v}{d x}=1+v+v^{2}-v$
$ \Rightarrow \quad x \cdot \frac{d v}{d x}=1+v^{2}\\ \Rightarrow \frac{d v}{1+v^{2}}=\frac{d x}{x} $
Integrating both sides, we get
$ \begin{aligned} \int \frac{d v}{1+v^{2}} & =\int \frac{d x}{x} \\ \Rightarrow \quad \tan ^{-1} v & =\log |x|+c \Rightarrow \tan ^{-1}(\frac{y}{x})=\log |x|+c \end{aligned} $
Hence, the required solution is $\tan ^{-1}(\frac{y}{x})=\log |x|+c$.
17. Find the general solution of the differential equation
$ (1+y^{2})+(x-e^{\tan ^{-1} y}) \frac{d y}{d x}=0 $
Show Answer
Solution
Given equation is
$ \begin{aligned} & (1+y^{2})+(x-e^{\tan ^{-1} y}) \frac{d y}{d x}=0 \\ \Rightarrow & (x-e^{\tan ^{-1} y}) \frac{d y}{d x}=-(1+y^{2}) \Rightarrow \frac{d y}{d x}=\frac{-(1+y^{2})}{x-e^{\tan ^{-1} y}} \\ \Rightarrow & \quad \frac{d x}{d y}=\frac{x-e^{\tan ^{-1} y}}{-(1+y^{2})} \Rightarrow \frac{d x}{d y}=-\frac{x}{(1+y^{2})}+\frac{e^{\tan ^{-1} y}}{1+y^{2}} \\ \Rightarrow & \frac{d x}{d y}+\frac{x}{(1+y^{2})}=\frac{e^{\tan ^{-1} y}}{1+y^{2}} \end{aligned} $
It is a linear differential equation of first order and first degree.
Here, $P=\frac{1}{1+y^{2}}$ and $Q=\frac{e^{\tan ^{-1} y}}{1+y^{2}}$
$\therefore$ Integrating factor I.F. $=e^{\int P d y}=e^{\int \frac{1}{1+y^{2}} d y}=e^{\tan ^{-1} y}$
$\therefore$ Solution is
$ \begin{aligned} & x \times \text{ I.F. }=\int Q \times \text{ I.F. } d y+c \\ \Rightarrow \quad x \cdot e^{\tan ^{-1} y} & =\int \frac{e^{\tan ^{-1} y}}{1+y^{2}} \cdot e^{\tan ^{-1} y} d y+c \end{aligned} $
Put $e^{\tan ^{-1} y}=t$
$\therefore e^{\tan ^{-1} y} \cdot \frac{1}{1+y^{2}} d y=d t$
$\therefore \quad x \cdot e^{\tan ^{-1} y}=\int t \cdot d t+c$
$\Rightarrow x \cdot e^{\tan ^{-1} y}=\frac{1}{2} t^{2}+c$
$ \begin{aligned} & \Rightarrow \quad x \cdot e^{\tan ^{-1} y}=\frac{1}{2}(e^{\tan ^{-1} y})^{2}+c \\ & \Rightarrow 2 x \cdot e^{\tan ^{-1} y}=(e^{\tan ^{-1} y})^{2}+2 c \\ & \Rightarrow 2 x \cdot e^{\tan ^{-1} y}=(e^{2\tan ^{-1} y})+ C, \quad (where \quad C = 2c) \end{aligned} $
Hence, this is the required general solution.
18. Find the general solution of $y^{2} d x+(x^{2}-x y+y^{2}) d y=0$.
Show Answer
Solution
The given equation is $y^{2} d x+(x^{2}-x y+y^{2}) d y=0$.
$ \begin{matrix} \Rightarrow & y^{2} d x=-(x^{2}-x y+y^{2}) d y \\ \Rightarrow & \frac{d x}{d y}=-\frac{x^{2}-x y+y^{2}}{y^{2}} \end{matrix} $
Since it is a homogeneous differential equation
$\therefore$ Put $x=v y \Rightarrow \frac{d x}{d y}=v+y \cdot \frac{d v}{d y}$
So, $\quad v+y \cdot \frac{d v}{d y}=-(\frac{v^{2} y^{2}-v y^{2}+y^{2}}{y^{2}})$
$\Rightarrow \quad v+y \cdot \frac{d v}{d y}=-\frac{y^{2}(v^{2}-v+1)}{y^{2}}$
$\Rightarrow \quad v+y \cdot \frac{d v}{d y}=(-v^{2}+v-1) \Rightarrow y \cdot \frac{d v}{d y}=-v^{2}+v-1-v$
$\Rightarrow \quad y \cdot \frac{d v}{d y}=-v^{2}-1 \Rightarrow \frac{d v}{(v^{2}+1)}=-\frac{d y}{y}$
Integrating both sides, we get
$ \begin{aligned} & \Rightarrow \quad \int \frac{d v}{(v^{2}+1)}=-\int \frac{d y}{y} \Rightarrow \tan ^{-1} v=-\log |y|+c \\ & \Rightarrow \quad \tan ^{-1}(\frac{x}{y})+\log |y|=c \end{aligned} $
Hence the required solution is $\tan ^{-1}(\frac{x}{y})+\log |y|=c$.
19. Solve: $(x+y)(d x-d y)=d x+d y$.
Show Answer
Solution
Given differential equation is
$\qquad (x+y)(d x-d y) =d x+d y$
$\Rightarrow \quad (x+y) d x-(x+y) d y =d x+d y$
$\Rightarrow \quad -(x+y) d y-d y =d x-(x+y) d x$
$ \begin{aligned} \Rightarrow \quad -(x+y+1) d y =-(x+y-1) d x \\ \Rightarrow \frac{d y}{d x} =\frac{x+y-1}{x+y+1} \end{aligned} $
Put $x+y=z$
$ \begin{aligned} \therefore \quad 1+\frac{d y}{d x} & =\frac{d z}{d x} \\ \frac{d y}{d x} & =\frac{d z}{d x}-1 \end{aligned} $
So, $\quad \frac{d z}{d x}-1=\frac{z-1}{z+1}$
$\Rightarrow \quad \frac{d z}{d x}=\frac{z-1}{z+1}+1 \Rightarrow \frac{d z}{d x}=\frac{z-1+z+1}{z+1}$
$\Rightarrow \quad \frac{d z}{d x}=\frac{2 z}{z+1} \quad \Rightarrow \frac{z+1}{z} d z=2 \cdot d x$
Integrating both sides, we get
$ \begin{aligned} & \int \frac{z+1}{z} d z=2 \int d x \\ & \Rightarrow \quad \int(1+\frac{1}{z}) d z=2 \int d x \\ & \Rightarrow \quad z+\log |z|=2 x+\log |c| \\ & \Rightarrow \quad x+y+\log |x+y|=2 x+\log |c| \\ & \Rightarrow \quad y+\log |x+y|=x+\log |c| \\ & \Rightarrow \quad \log |x+y|=x-y+\log |c| \\ & \Rightarrow \log |x+y|-\log |c|=(x-y) \\ & \Rightarrow \quad \log |\frac{x+y}{c}|=(x-y) \Rightarrow |\frac{x+y}{c}|=e^{x-y} \\ & \quad x+y=\pm c \cdot e^{x-y} \\ & \therefore \quad x+y=C \cdot e^{x-y}, \quad (where \quad C = \pm c) \end{aligned} $
Hence, the required solution is $x+y=C \cdot e^{x-y}$.
20. Solve: $2(y+3)-x y \cdot \frac{d y}{d x}=0$, given that $y(1)=-2$.
Show Answer
Solution
Given differential equation is
$ \begin{aligned} 2(y+3)-x y \cdot \frac{d y}{d x} & =0 \\ \Rightarrow \quad x y \cdot \frac{d y}{d x} & =2 y+6 \\ \Rightarrow \quad(\frac{y}{2 y+6}) d y & =\frac{d x}{x} \Rightarrow \frac{1}{2}(\frac{y}{y+3}) d y=\frac{d x}{x} \end{aligned} $
Integrating both sides, we get
$ \begin{aligned} & \Rightarrow \quad \frac{1}{2} \int \frac{y}{y+3} \cdot d y=\int \frac{d x}{x} \Rightarrow \frac{1}{2} \int \frac{y+3-3}{y+3} d y=\int \frac{d x}{x} \\ & \Rightarrow \quad \frac{1}{2} \int(1-\frac{3}{y+3}) d y=\int \frac{d x}{x} \end{aligned} $
$ \begin{aligned} & \Rightarrow \frac{1}{2} \int 1 \cdot d y-\frac{3}{2} \int \frac{1}{y+3} d y=\int \frac{d x}{x} \\ & \Rightarrow \quad \frac{1}{2} y-\frac{3}{2} \log |y+3|=\log|x|+\log |c| \\ & \Rightarrow \quad \frac{1}{2} y-\frac{3}{2} \log |y+3|=\log|xc| \\ & \Rightarrow \quad y-{3} \log |y+3|=2\log|xc| \\ & \Rightarrow \quad y-{3} \log |y+3|=\log(|xc|)^{2} \\ & \Rightarrow \quad y= \log (|y+3|)^{3}+\log(|xc|)^{2} \\ & \Rightarrow \quad y= \log (|y+3|)^{3}+\log(xc)^{2} \\ & \Rightarrow \quad y= \log ((xc)^{2}(|y+3|)^{3}) \\ & \Rightarrow \quad e^{y}= ((xc)^{2}(|y+3|)^{3}) \\ & \Rightarrow \quad x^{2}|y+3|^{3}=\frac {1}{c^{2}} e^{y} \\ & \Rightarrow \quad x^{2}(y+3)^{3}=\pm \frac {1}{c^{2}} e^{y} \\ & \Rightarrow \quad x^{2}(y+3)^{3}=C e^{y},(where \quad C=\pm \frac {1}{c^{2}}) \end{aligned} $
Put $x=1, y=-2$
$ \Rightarrow \quad 1^{2}(-2+3)^{3} =C e^{-2} $
$ \Rightarrow \quad C=e^{2}$
$ \therefore$ equation is
$ \Rightarrow x^{2}(y+3)^{3}=e^{y+2}$
Hence, the required solution is $x^{2}(y+3)^{3}=e^{y+2}$.
21. Solve the differential equation $d y=cos x \text {(2-y cosec x)} d x$ given that $y=2$ when $x=\frac{\pi}{2}$.
Show Answer
Solution
The given differential equation is
$ d y=\cos x \text{(2-y cosec x)} d x $
$\Rightarrow \frac{d y}{d x}=\cos x\text {(2-y cosec x)} \Rightarrow \frac{d y}{d x}=2 \cos x-y \cos x \cdot \frac{1}{sinx}$
$\Rightarrow \frac{d y}{d x}=2 \cos x-y \cot x \Rightarrow \frac{d y}{d x}+y \cot x=2 \cos x$
It is a linear differential equation of first order and first degree.
Here, $P=\cot x$ and $Q=2 \cos x$.
$\therefore$ Integrating factor I.F. $=e^{\int P d x}=e^{\int \cot x d x}=e^{\log |\sin x|}=\sin x , \quad (\sin x>0)$
$\therefore$ Required solution is $y \times$ I.F $=\int Q \times$ I.F. $d x+c$ $\Rightarrow y \cdot \sin x=\int 2 \cos x \cdot \sin x d x+c$
$\Rightarrow y \cdot \sin x=\int \sin 2 x d x+c \Rightarrow y \cdot \sin x=-\frac{1}{2} \cos 2 x+c$
Put $x=\frac{\pi}{2}$ and $y=2$, we get
$ \begin{aligned} 2 \sin \frac{\pi}{2} & =-\frac{1}{2} \cos \pi+c \\ \Rightarrow \quad 2(1) & =-\frac{1}{2}(-1)+c \Rightarrow 2=\frac{1}{2}+c \Rightarrow c=2-\frac{1}{2}=\frac{3}{2} \end{aligned} $
$\therefore$ The equation is $y \sin x=-\frac{1}{2} \cos 2 x+\frac{3}{2}$.
22. Form the differential equation by eliminating $A$ and $B$ in $A x^{2}+B y^{2}=1$.
Show Answer
Solution
Given that $A x^{2}+B y^{2}=1$
Differentiating w.r.t. $x$, we get
$\qquad 2 A \cdot x+2 B y \frac{d y}{d x} =0$
$\Rightarrow \qquad A x+B y \cdot \frac{d y}{d x} =0 \Rightarrow B y \cdot \frac{d y}{d x}=-A x$
$\therefore \qquad \frac{y}{x} \cdot \frac{d y}{d x} =-\frac{A}{B}$
Differentiating both sides again w.r.t. $x$, we have
$ \begin{aligned} & \frac{y}{x} \cdot \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}(\frac{x \cdot \frac{d y}{d x}-y \cdot 1}{x^{2}})=0 \\ \Rightarrow & \frac{y x^{2}}{x} \cdot \frac{d^{2} y}{d x^{2}}+x \cdot(\frac{d y}{d x})^{2}-y \cdot \frac{d y}{d x}=0 \\ \Rightarrow & x y \cdot \frac{d^{2} y}{d x^{2}}+x \cdot(\frac{d y}{d x})^{2}-y \cdot \frac{d y}{d x}=0 \Rightarrow x y \cdot y^{\prime \prime}+x \cdot(y^{\prime})^{2}-y \cdot y^{\prime}=0 \end{aligned} $
Hence, the required equation is
$ x y \cdot y^{\prime \prime}+x \cdot(y^{\prime})^{2}-y \cdot y^{\prime}=0 $
23. Solve the differential equation $(1+y^{2}) \tan ^{-1} x d x+2 y(1+x^{2}) d y=0$.
Show Answer
Solution
Given differential equation is
$ \begin{matrix} (1+y^{2}) \tan ^{-1} x d x+2 y(1+x^{2}) d y=0 \\ \Rightarrow \qquad 2 y(1+x^{2}) d y=-(1+y^{2}) \cdot \tan ^{-1} x \cdot d x \\ \Rightarrow \qquad \frac{2 y}{1+y^{2}} d y=-\frac{\tan ^{-1} x}{1+x^{2}} \cdot d x \end{matrix} $
Integrating both sides, we get
$\int \frac{2 y}{1+y^{2}} d y =-\int \frac{\tan ^{-1} x}{1+x^{2}} \cdot d x $
$ let \quad 1+y^{2} = t $
$ 2y dy = dt $
$ and \quad \tan ^{-1} x = k $
$ \frac{1} {1+x^{2}} dx = dk $
$\therefore \int \frac {dt}{t} = -\int kdk $
$ log |t| =- \frac {k^{2}}{2} + c $
$\Rightarrow \quad \log |1+y^{2}| =-\frac{1}{2}(\tan ^{-1} x)^{2}+c$
$\Rightarrow \quad \frac{1}{2}(\tan ^{-1} x)^{2}+\log |1+y^{2}|=c$
$\Rightarrow \quad \frac{1}{2}(\tan ^{-1} x)^{2}+\log (1+y^{2})=c, \quad (\because (1+y)^{2} \quad is \quad positive)$
Which is the required solution.
24. Find the differential equation of system of concentric circles with centre $(1,2)$.
Show Answer
Solution
Family of concentric circles with centre $(1,2)$ and radius ’ $r$ ’ is
$ (x-1)^{2}+(y-2)^{2}=r^{2} $
Differentiating both sides w.r.t., $x$ we get
$ 2(x-1)+2(y-2) \frac{d y}{d x}=0 \Rightarrow(x-1)+(y-2) \frac{d y}{d x}=0 $
Which is the required equation.
Long Answer Type Questions
25. Solve: $y+\frac{d}{d x}(x y)=x(\sin x+\log x)$
Show Answer
Solution
The given differential equation is
$ \begin{aligned} & y+\frac{d}{d x}(x y)=x(\sin x+\log x) \\ & \Rightarrow \quad y+x \cdot \frac{d y}{d x}+y=x(\sin x+\log x) \\ & \Rightarrow \quad x \frac{d y}{d x}=x(\sin x+\log x)-2 y \\ & \Rightarrow \quad \frac{d y}{d x}=(\sin x+\log x)-\frac{2 y}{x} \Rightarrow \frac{d y}{d x}+\frac{2}{x} y=(\sin x+\log x) \end{aligned} $
It is a linear differential equation of first order and first degree.
Here, $P=\frac{2}{x}$ and $Q=(\sin x+\log x)$
Integrating factor I.F. $=e^{\int P d x}=e^{\int \frac{2}{x} d x}=e^{2 \log |x|}=e^{\log |x|^{2}}=|x|^{2}= x^{2}$
$\therefore$ Solution is
$$ \begin{align*} y \times \text{ I.F. } & =\int Q \times \text{ I.F. } d x+c \\ \Rightarrow \quad y \cdot x^{2} & =\int(\sin x+\log x) x^{2} d x+c \tag{1}\\ \Rightarrow \quad y \cdot x^{2} & = \text {I +c } \end{align*} $$
Let I
$ \begin{aligned} & =\int(\sin x+\log x) x^{2} d x \\ & =\int x^{2} \sin x d x+\int x^{2} \log x d x \\ & (Integration \quad by \quad parts) \\ & \begin{aligned} = & {[x^{2} \cdot \int \sin x d x-\int(D(x^{2}) \cdot \int \sin x d x) d x]+} {[\log x \cdot \int x^{2} d x-\int(D(\log x) \cdot \int x^{2} d x) d x] } \end{aligned} \\ & =[x^{2}(-\cos x)-2 \int-x \cos x d x]+[\log x \cdot \frac{x^{3}}{3}-\int \frac{1}{x} \cdot \frac{x^{3}}{3} d x] \\ & =[-x^{2} \cos x+2(x \sin x-\int 1 \cdot \sin x d x)]+[\frac{x^{3}}{3} \log x-\frac{1}{3} \int x^{2} d x] \\ & =-x^{2} \cos x+2 x \sin x+2 \cos x+\frac{x^{3}}{3} \log x-\frac{1}{9} x^{3} \end{aligned} $
Now from eq (1) we get,
$ \begin{aligned} y \cdot x^{2} & =-x^{2} \cos x+2 x \sin x+2 \cos x+\frac{x^{3}}{3} \log x-\frac{1}{9} x^{3}+c \\ \therefore \quad & y=-\cos x+\frac{2 \sin x}{x}+\frac{2 \cos x}{x^{2}}+\frac{x \log x}{3}-\frac{1}{9} x+c \cdot x^{-2} \end{aligned} $
Hence, the required solution is
$ y=-\cos x+\frac{2 \sin x}{x}+\frac{2 \cos x}{x^{2}}+\frac{x \log x}{3}-\frac{1}{9} x+c \cdot x^{-2} $
26. Find the general solution of $(1+\tan y)(d x-d y)+2 x d y=0$.
Show Answer
Solution
Given that: $(1+\tan y)(d x-d y)+2 x d y=0$
$\Rightarrow \quad(1+\tan y) d x-(1+\tan y) d y+2 x d y=0$
$ \Rightarrow \quad(1+\tan y) d x-(1+\tan y-2 x) d y=0 $
$ \begin{aligned} & \Rightarrow \quad(1+\tan y) \frac{d x}{d y}=(1+\tan y-2 x) \Rightarrow \frac{d x}{d y}=\frac{1+\tan y-2 x}{1+\tan y} \\ & \Rightarrow \quad \frac{d x}{d y}=1-\frac{2 x}{1+\tan y} \Rightarrow \frac{d x}{d y}+\frac{2 x}{1+\tan y}=1 \end{aligned} $
It is a linear differential equation of first order and first degree.
Here, $P=\frac{2}{1+\tan y}$ and $Q=1$
Integrating factor I.F.
$ \begin{aligned} & =e^{\int \frac{2}{1+\tan y} d y}=e^{\int \frac{2 \cos . y}{\sin y+\cos y} d y} \\ & =e^{\int \frac{\sin y+\cos y-\sin y+\cos y}{(\sin y+\cos y)} d y}=e^{\int(1+\frac{\cos y-\sin y}{\sin y+\cos y}) d y} \\ & =e^{\int 1 \cdot d y} \cdot e^{\int \frac{\cos y-\sin y}{\sin y+\cos y} d y} \\ & =e^{y} \cdot e^{\log |(\sin y+\cos y)|}=e^{y} \cdot(\sin y+\cos y), \quad ((\sin y+\cos y)>0) \end{aligned} $
So, the solution is $\quad x \times$ I.F. $=\int Q \times$ I.F. $d y+c$
$\Rightarrow x \cdot e^{y}(\sin y+\cos y)=\int 1 \cdot e^{y}(\sin y+\cos y) d y+c$
$\Rightarrow \quad x \cdot e^{y}(\sin y+\cos y)=e^{y} \cdot \sin y+c$
$ [\because \int e^{x}[f(x)+f^{\prime}(x)] d x=e^{x} f(x)+c] $
$\Rightarrow \quad x(\sin y+\cos y)=\sin y+c \cdot e^{-y}$
Hence, the required solution is $x(\sin y+\cos y)=\sin y+c \cdot e^{-y}$.
27. Solve : $\frac{d y}{d x}=\cos (x+y)+\sin (x+y)$. [Hint: Substitute $x+y=z$ ]
Show Answer
Solution
Given that : $\frac{d y}{d x}=\cos (x+y)+\sin (x+y)$
Put $\quad x+y=v$, on differentiating w.r.t. $x$, we get,
$1+\frac{d y}{d x} =\frac{d v}{d x}$
$\therefore \quad \frac{d y}{d x} =\frac{d v}{d x}-1$
$\therefore \quad \frac{d v}{d x}-1 =\cos v+\sin v$
$\Rightarrow \quad \frac{d v}{d x} =\cos v+\sin v+1$
$\Rightarrow \quad \frac{d v}{\cos v+\sin v+1} = d x $
$\Rightarrow \quad \frac{d v}{(\frac{1-\tan ^{2} \frac{v}{2}}{1+\tan ^{2} \frac{v}{2}}+\frac{2 \tan \frac{v}{2}}{1+\tan ^{2} \frac{v}{2}}+1)} = d x $
$\Rightarrow \quad \frac{(1+\tan ^{2} \frac{v}{2})}{1-\tan ^{2} \frac{v}{2}+2 \tan \frac{v}{2}+1+\tan ^{2} \frac{v}{2}} d v = d x $
Integrating \quad both \quad sides, we \quad have $
$\Rightarrow \quad \int \frac{\sec ^{2} \frac{v}{2}}{2+2 \tan \frac {v}{2}} d v =\int 1 . d x $
$\text{ Put } \quad 2+2 \tan \frac{v}{2} = t$
$2 \cdot \frac{1}{2} \sec ^{2} \frac{v}{2} d v =d t \Rightarrow \sec ^{2} \frac{v}{2} d v=d t $
$\int \frac{d t}{t} =\int 1 \cdot d x $
$\Rightarrow \quad \log |t| =x+c $
$\Rightarrow \quad \log |2+2 \tan \frac{v}{2}| =x+c $
$\Rightarrow \quad \log |2+2 \tan (\frac{x+y}{2})|=x+c \Rightarrow \log 2(|1+\tan (\frac{x+y}{2})|)=x+c $
$\Rightarrow \quad \log 2+\log (|1+\tan (\frac{x+y}{2})|) =x+c $
$\Rightarrow \quad \log (|1+\tan (\frac{x+y}{2})|) =x+c-\log 2$
Hence, the required solution is
$ \log (|1+\tan (\frac{x+y}{2})|)=x+K \quad[c-\log 2=K] $
28. Find the general solution of $\frac{d y}{d x}-3 y=\sin 2 x$.
Show Answer
Solution
Given equation is $\frac{d y}{d x}-3 y=\sin 2 x$.
It is a linear differential equation of first order and first degree.
Here, $P=-3$ and $Q=\sin 2 x$
$\therefore$ Integrating factor I.F. $=e^{\int P d x}=e^{\int-3 d x}=e^{-3 x}$
$\therefore$ Solution is
$ \begin{aligned} & y \times \text{ I.F. }=\int Q \times \text{ I.F. } d x+c \\ & \Rightarrow \quad y \cdot e^{-3 x}=\int \sin 2 x \cdot e^{-3 x} d x+c \\ & \text{ Let } \quad I=\int \sin 2 x \cdot e^{-3 x} d x \\ Integration \quad by \quad part \\ & \Rightarrow \quad I=\sin 2 x \cdot \int e^{-3 x} d x-\int(D(\sin 2 x) \cdot \int e^{-3 x} d x) d x \\ & \Rightarrow \quad I=\sin 2 x \cdot \frac{e^{-3 x}}{-3}-\int 2 \cos 2 x \cdot \frac{e^{-3 x}}{-3} d x \\ & \Rightarrow \quad I=\frac{e^{-3 x}}{-3} \sin 2 x+\frac{2}{3} \int {\cos 2 x} \cdot e^{-3 x} d x \\ & \Rightarrow \quad I=\frac{e^{-3 x}}{-3} \sin 2 x+\frac{2}{3}[\cos 2 x \cdot \int e^{-3 x} d x-\int[D (\cos 2 x) \cdot \int e^{-3 x} d x] d x] \end{aligned} $
$ \begin{aligned} \Rightarrow \quad I & =\frac{e^{-3 x}}{-3} \sin 2 x+\frac{2}{3}[\cos 2 x \cdot \frac{e^{-3 x}}{-3}- \int -2 \sin 2 x \cdot \frac{e^{-3 x}}{-3}] d x \\ \Rightarrow \quad I & =\frac{e^{-3 x}}{-3} \sin 2 x-\frac{2}{9} \cos 2 x \cdot e^{-3 x}-\frac{4}{9} \int \sin 2 x \cdot e^{-3 x} d x \\ \Rightarrow \quad & =\frac{e^{-3 x}}{-3} \sin 2 x-\frac{2}{9} e^{-3 x} \cos 2 x-\frac{4}{9} I \\ \Rightarrow \quad I+\frac{4}{9} I & =\frac{e^{-3 x}}{-3} \sin 2 x-\frac{2}{9} e^{-3 x} \cos 2 x \\ \Rightarrow \quad \frac{13 I}{9} & =-\frac{1}{9}[3 e^{-3 x} \sin 2 x+2 e^{-3 x} \cos 2 x] \\ \Rightarrow \quad I & =-\frac{1}{13} e^{-3 x}[3 \sin 2 x+2 \cos 2 x] \end{aligned} $
$\therefore$ The equation becomes
$ \begin{aligned} y \cdot e^{-3 x} & =-\frac{1}{13} e^{-3 x}[3 \sin 2 x+2 \cos 2 x]+c \\ \therefore \quad y & =-\frac{1}{13}[3 \sin 2 x+2 \cos 2 x]+c \cdot e^{3 x} \end{aligned} $
Hence, the required solution is
$ y=-[\frac{3 \sin 2 x+2 \cos 2 x}{13}]+c \cdot e^{3 x} $
29. Find the equation of a curve passing through $(2,1)$ if the slope of the tangent to the curve at any point $(x, y)$ is $\frac{x^{2}+y^{2}}{2 x y}$.
Show Answer
Solution
Given that the slope of tangent to a curve at $(x, y)$ is
$ \frac{d y}{d x}=\frac{x^{2}+y^{2}}{2 x y} $
It is a homogeneous differential equation
So, put $y=v x \Rightarrow \frac{d y}{d x}=v+x \cdot \frac{d v}{d x}$
$ v+x \cdot \frac{d v}{d x}=\frac{x^{2}+v^{2} x^{2}}{2 x \cdot v x} $
$ \begin{aligned} & \Rightarrow \quad v+x \cdot \frac{d v}{d x}=\frac{1+v^{2}}{2 v} \\ & \Rightarrow \quad x \cdot \frac{d v}{d x}=\frac{1+v^{2}}{2 v}-v \Rightarrow x \cdot \frac{d v}{d x}=\frac{1+v^{2}-2 v^{2}}{2 v} \\ & \Rightarrow \quad x \cdot \frac{d v}{d x}=\frac{1-v^{2}}{2 v} \Rightarrow \frac{2 v}{1-v^{2}} d v=\frac{d x}{x} \end{aligned} $
Integrating both sides, we get
$ \begin{gathered} \int \frac{2 v}{1-v^{2}} d v=\int \frac{d x}{x} \Rightarrow-\log |1-v^{2}|=\log |x|+\log |C| \\ \Rightarrow-\log |1-\frac{y^{2}}{x^{2}}|=\log |x|+\log |C| \Rightarrow-\log |\frac{x^{2}-y^{2}}{x^{2}}|=\log |x|+\log |C| \\ \Rightarrow \log |\frac{x^{2}}{x^{2}-y^{2}}|=\log |x C| \Rightarrow \frac{x^{2}}{x^{2}-y^{2}}=\pm Cx \\ \Rightarrow \frac{x^{2}}{x^{2}-y^{2}}=cx, \quad (where \quad c = \pm C) \end{gathered} $
Since, the curve is passing through the point $(2,1)$
$ \therefore \quad \frac{(2)^{2}}{(2)^{2}-(1)^{2}}=2 c \Rightarrow \frac{4}{3}=2 c \Rightarrow c=\frac{2}{3} $
Hence, the required equation is
$ \frac{x^{2}}{x^{2}-y^{2}}=\frac{2}{3} x \Rightarrow 2(x^{2}-y^{2})=3 x $
30. Find the equation of the curve through the point $(1,0)$ if the slope of the tangent to the curve at any point $(x, y)$ is $\frac{y-1}{x^{2}+x}$.
Show Answer
Solution
Given that the slope of the tangent to the curve at $(x, y)$ is
$ \frac{d y}{d x}=\frac{y-1}{x^{2}+x} \Rightarrow \frac{d y}{y-1}=\frac{d x}{x^{2}+x} $
Integrating both sides, we have
$ \begin{aligned} & \int \frac{d y}{y-1}=\int \frac{d x}{x^{2}+x} \\ & \Rightarrow \quad \int \frac{d y}{y-1}=\int \frac{d x}{x^{2}+x+\frac{1}{4}-\frac{1}{4}} \text{ [making perfect square] } \\ & \Rightarrow \quad \int \frac{d y}{y-1}=\int \frac{d x}{(x+\frac{1}{2})^{2}-(\frac{1}{2})^{2}} \end{aligned} $
$ \begin{matrix} \Rightarrow & \log |y-1|=\frac{1}{2 \times \frac{1}{2}} \log |\frac{x+\frac{1}{2}-\frac{1}{2}}{x+\frac{1}{2}+\frac{1}{2}}|+\log |c| \\ \Rightarrow & \log |y-1|=\log |\frac{x}{x+1}|+\log |c| \\ \Rightarrow & \log |y-1|=\log |c(\frac{x}{x+1})| \\ \therefore & |y-1|=|\frac{c x}{x+1}| \\ \therefore & y-1=\pm \frac{c x}{x+1} \\ \Rightarrow & (y-1)(x+1)=C x , \quad (where \quad C= \pm c) \end{matrix} $
Since, the line is passing through the point $(1,0)$, then $(0-1)(1+1)=C(1) \Rightarrow C=-2$.
$(y-1)(x+1)=-2 x$.
Hence, the required solution is $(y-1)(x+1)+2 x=0$.
31. Find the equation of a curve passing through origin if the slope of the tangent to the curve at any point $(x, y)$ is equal to the square of the difference of the abscissa and ordinate of the point.
Show Answer
Solution
Here, slope of the tangent of the curve $=\frac{d y}{d x}$ and the difference between the abscissa and ordinate $=x-y$.
$\therefore$ As per the condition, $\frac{d y}{d x}=(x-y)^{2}$
Put $x-y=v$
$ \begin{aligned} & 1-\frac{d y}{d x}=\frac{d v}{d x} \\ & \therefore \quad \frac{d y}{d x}=1-\frac{d v}{d x} \end{aligned} $
$\therefore$ the equation becomes
$ 1-\frac{d v}{d x}=v^{2} \Rightarrow \frac{d v}{d x}=1-v^{2} \Rightarrow \frac{d v}{1-v^{2}}=d x $
Integrating both sides, we get
$$ \begin{align*} \int \frac{d v}{1-v^{2}} & =\int d x \\ \Rightarrow \quad \frac{1}{2} \log |\frac{1+v}{1-v}| & =x+c \quad \Rightarrow \quad \frac{1}{2} \log |\frac{1+x-y}{1-x+y}|=x+c \\ \Rightarrow \quad |\frac{1+x-y}{1-x+y}|=e^{2(x+c)} \\ \Rightarrow \quad |\frac{1+x-y}{1-x+y}|=e^{2c}e^{2x} \\ \Rightarrow \quad \frac{1+x-y}{1-x+y}=\pm e^{2c}e^{2x} \\ \Rightarrow \quad \frac{1+x-y}{1-x+y}=\pm e^{2c}e^{2x} \\ \Rightarrow \quad \frac{1+x-y}{1-x+y}=Ce^{2x} (where C= \pm e^{2c}) \end{align*} $$
Since, the curve is passing through $(0,0)$
$ \Rightarrow \frac{1+0-0}{1-0+0} =Ce^{ 0} $
$ \Rightarrow C=1 $
$ \begin{aligned} & \therefore & \frac{1+x-y}{1-x+y} & =e^{2 x} \\ \Rightarrow & & (1+x-y) & =e^{2 x}(1-x+y) \end{aligned} $
Hence, the required equation is $(1+x-y)=e^{2 x}(1-x+y)$.
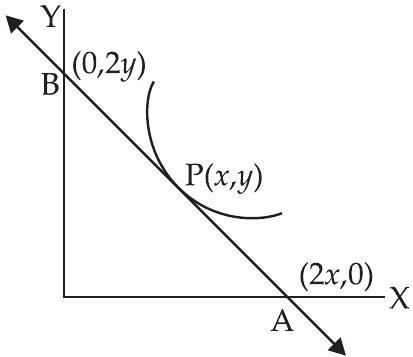
32. Find the equation of a curve passing through the point $(1,1)$, if the tangent drawn at any point $P(x, y)$ on the curve meets the coordinate axes at $A$ and $B$ such that $P$ is the mid point of $AB$.
Show Answer
Solution
Let $P(x, y)$ be any point on the curve and $AB$ be the tangent to the given curve at $P$.
$P$ is the mid point of $A B$ (given)
$\therefore$ Coordinates of $A$ and $B$ are $(2 x, 0)$ and $(0,2 y)$ respectively.
$\therefore$ Slope of the tangent
$ AB= $
$ \begin{aligned} & \frac{2 y-0}{0-2 x}=-\frac{y}{x} \\ & \therefore \quad \frac{d y}{d x}=-\frac{y}{x} \Rightarrow \frac{d y}{y}=-\frac{d x}{x} \end{aligned} $
Integrating both sides, we get
$ \begin{aligned} & \int \frac{d y}{y}=-\int \frac{d x}{x} \Rightarrow \log |y|=-\log |x|+\log |c| \\ & \Rightarrow \quad \log |y|+\log |x|=\log |c| \quad \Rightarrow \log |y x|=\log|c| \\ & \therefore \quad |y x|=|c| \\ & \therefore \quad y x=\pm c \\ & \therefore \quad y x=C , \quad (where \quad C = \pm c) \end{aligned} $
Since, the curve passes through $(1,1)$
$ \begin{aligned} \therefore & & 1 \times 1 & =C\quad \therefore \quad C=1 \\ \Rightarrow & & y x & =1 \end{aligned} $
Hence, the required equation is $x y=1$.
33. Solve: $x \frac{d y}{d x}=y(\log y-\log x+1)$
Show Answer
Solution
Given that: $x \frac{d y}{d x}=y(\log y-\log x+1)$
$ \Rightarrow \quad x \frac{d y}{d x}=y[\log (\frac{y}{x})+1] \Rightarrow \frac{d y}{d x}=\frac{y}{x}[\log (\frac{y}{x})+1] $
Since, it is a homogeneous differential equation.
$\therefore$ Put $y=v x \Rightarrow \frac{d y}{d x}=v+x \cdot \frac{d v}{d x}$
$\therefore \quad v+x \cdot \frac{d v}{d x}=\frac{v x}{x}[\log (\frac{v x}{x})+1]$
$\Rightarrow \quad v+x \cdot \frac{d v}{d x}=v[\log v+1]$
$\Rightarrow \quad x \cdot \frac{d v}{d x}=v[\log v+1]-v \Rightarrow x \cdot \frac{d v}{d x}=v[\log v+1-1]$
$\Rightarrow \quad x \cdot \frac{d v}{d x}=v \cdot \log v \Rightarrow \frac{d v}{v \log v}=\frac{d x}{x}$
Integrating both sides, we get
$ \qquad \int \frac{d v}{v \log v}=\int \frac{d x}{x} $
Put $\log v=t$ on L.H.S.
$ \begin{matrix} \frac{1}{v} d v =dt \\ \therefore \quad \int \frac{d t}{t} =\int \frac{d x}{x} \\ \log |t| =\log |x|+\log |C| \\ \Rightarrow \quad \log |\log v| =\log |x C| \Rightarrow |\log v|=|x C| \\ \Rightarrow \quad \log (\frac{y}{x}) =\pm Cx\\ \Rightarrow \quad \log (\frac{y}{x}) =cx, \quad where \quad c = \pm C \end{matrix} $
Hence, the required solution is $\log (\frac{y}{x})=x c$.
Objective Type Questions
34. The degree of the differential equation
$ (\frac{d^{2} y}{d x^{2}})^{2}+(\frac{d y}{d x})^{2}=x \sin (\frac{d y}{d x}) \text{ is } $
(a) 1
(b) 2
(c) 3
(d) not defined
Show Answer
Solution
The degree of the given differential equation is not defined because the value of $\sin (\frac{d y}{d x})$ on expansion will be in increasing power of $(\frac{d y}{d x})$.
-
Option (a) 1: This is incorrect because the degree of a differential equation is defined as the highest power of the highest order derivative, provided the equation is polynomial in derivatives. In this case, the equation involves a trigonometric function of the derivative, making it non-polynomial.
-
Option (b) 2: This is incorrect because, although the highest power of the second-order derivative is 2, the presence of the trigonometric function $\sin (\frac{d y}{d x})$ means the equation is not polynomial in its derivatives, so the degree is not defined.
-
Option (c) 3: This is incorrect because, although the highest power of the second-order derivative is 2, the presence of the trigonometric function $\sin (\frac{d y}{d x})$ means the equation is not polynomial in its derivatives, so the degree is not defined.
35. The degree of the differential equation $[1+(\frac{d y}{d x})^{2}]^{3 / 2}=\frac{d^{2} y}{d x^{2}}$ is
(a) 4
(b) $\frac{3}{2}$
(c) not defined
(d) 2
Show Answer
Solution
The given differential equation is
$ [1+(\frac{d y}{d x})^{2}]^{3 / 2}=(\frac{d^{2} y}{d x^{2}}) $
Squaring both sides, we have
$ [1+(\frac{d y}{d x})^{2}]^{3}=(\frac{d^{2} y}{d x^{2}})^{2} $
So, the degree of the given differential equation is 2 .
Hence, the correct option is $(d)$.
36. The order and degree of the differential equation $\frac{d^{2} y}{d x^{2}}+(\frac{d y}{d x})^{\frac{1}{4}}+x^{\frac{1}{5}}=0$ respectively are
(a) 2 and 4
(b) 2 and not defined
(c) 2 and 3
(d) 3 and 3
Show Answer
Solution
Given that, $\quad \frac{d^2 y}{d x^2}+\left(\frac{d y}{d x}\right)^{1 / 4}=-x^{1 / 5}$
$ \begin{aligned} & \Rightarrow \quad \frac{d^2 y}{d x^2}+\left(\frac{d y}{d x}\right)^{1 / 4}=-x^{1 / 5} \ & \Rightarrow \quad\left(\frac{d y}{d x}\right)^{1 / 4}=-\left(x^{1 / 5}+\frac{d^2 y}{d x^2}\right) \end{aligned} $
On squaring both sides, we get
$ \left(\frac{d y}{d x}\right)^{1 / 2}=\left(x^{1 / 5}+\frac{d^2 y}{d x^2}\right)^2 $
Again, on sqaring both sides, we have
$ \frac{d y}{d x}=\left(x^{1 / 5}+\frac{d^2 y}{d x^2}\right)^4 $
order $=2$, degree $=4$
Hence, the correct option is $(a)$.
37. If $y=e^{-x}(A \cos x+B \sin x)$, then $y$ is a solution of
(a) $\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0$
(b) $\frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+2 y=0$
(c) $\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}+2 y=0$
(d) $\frac{d^{2} y}{d x^{2}}+2 y=0$
Show Answer
Solution
Given equation is $y=e^{-x}(A \cos x+B \sin x)$
Differentiating both sides, w.r.t. $x$, we get
$ \begin{aligned} & \frac{d y}{d x}=e^{-x}(-A \sin x+B \cos x)-e^{-x}(A \cos x+B \sin x) \\ & \frac{d y}{d x}=e^{-x}(-A \sin x+B \cos x)-y \end{aligned} $
Again differentiating w.r.t. $x$, we get
$ \begin{aligned} & \frac{d^{2} y}{d x^{2}}=e^{-x}(-A \cos x-B \sin x)-e^{-x}(-A \sin x+B \cos x)-\frac{d y}{d x} \\ \Rightarrow & \frac{d^{2} y}{d x^{2}}=-e^{-x}(A \cos x+B \sin x)-[\frac{d y}{d x}+y]-\frac{d y}{d x} \\ \Rightarrow & \frac{d^{2} y}{d x^{2}}=-y-\frac{d y}{d x}-y-\frac{d y}{d x} \\ \Rightarrow & \frac{d^{2} y}{d x^{2}}=-2 \frac{d y}{d x}-2 y \Rightarrow \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}+2 y=0 \end{aligned} $
Hence, the correct option is (c)
38. The differential equation for $y=A \cos \alpha x+B \sin \alpha x$, where $A$ and $B$ are arbitrary constants is:
(a) $\frac{d^{2} y}{d x^{2}}-\alpha^{2} y=0$
(b) $\frac{d^{2} y}{d x^{2}}+\alpha^{2} y=0$
(c) $\frac{d^{2} y}{d x^{2}}+\alpha y=0$
(d) $\frac{d^{2} y}{d x^{2}}-\alpha y=0$
Show Answer
Solution
Given equation is : $y=A \cos \alpha x+B \sin \alpha x$ Differentiating both sides w.r.t. $x$, we have
$ \begin{aligned} \frac{d y}{d x} & =-A \sin \alpha x \cdot \alpha+B \cos \alpha x \cdot \alpha \\ & =-A \alpha \sin \alpha x+B \alpha \cos \alpha x \end{aligned} $
Again differentiating w.r.t. $x$, we get
$ \begin{aligned} \frac{d^{2} y}{d x^{2}} & =-A \alpha^{2} \cos \alpha x-B \alpha^{2} \sin \alpha x \\ \Rightarrow \quad \frac{d^{2} y}{d x^{2}} & =-\alpha^{2}(A \cos \alpha x+B \sin \alpha x) \\ \Rightarrow \quad \frac{d^{2} y}{d x^{2}} & =-\alpha^{2} y \Rightarrow \frac{d^{2} y}{d x^{2}}+\alpha^{2} y=0 \end{aligned} $
Hence, the correct option is (b).
39. Solution of differential equation $x d y-y d x=0$ represents:
(a) a rectangular hyperbola
(b) parabola whose vertex is at origin
(c) straight line passing through origin
(d) a circle whose centre is at origin.
Show Answer
Solution
The given differential equation is
$ x d y-y d x=0 $
$ \Rightarrow \quad \frac{d y}{d x}=\frac{y}{x} \Rightarrow \frac{d y}{y}=\frac{d x}{x} $
Integrating both sides, we get
$
\begin{aligned}
& \qquad \int \frac{d y}{y}=\int \frac{d x}{x} \\
& \Rightarrow \quad \log |y|=\log |x|+\log|c| \Rightarrow \log |y|=\log |x c| \\
& \Rightarrow \quad |y|=|x c| \\
& \Rightarrow \quad y =\pm cx \\
& \Rightarrow \quad y =Cx \quad where \quad C = \pm c
& \text{ which is a straight line passing through the origin. } \\
& \text{ Hence, the correct answer is }(c)
\end{aligned}
$
40. Integrating factor of the differential equation $\cos x \cdot \frac{d y}{d x}+y \sin x=1$ is
(a) $\cos x$
(b) $\tan x$
(c) $\sec x$
(d) $\sin x$
Show Answer
Solution
The given differential equation is
$ \begin{aligned} \cos x \cdot \frac{d y}{d x}+y \sin x =1 \\ \Rightarrow \qquad \frac{d y}{d x}+\frac{\sin x}{\cos x} y =\frac{1}{\cos x} \Rightarrow \frac{d y}{d x}+\tan x y=\sec x \end{aligned} $
Here, $P=\tan x$ and $Q=\sec x$
$\therefore$ Integrating factor $=e^{\int P d x}=e^{\int \tan x d x}=e^{\log |\sec x|}=\sec x ,\quad (\sec x >0)$
Hence, the correct option is (c).
41. Solution of differential equation $\tan y \sec ^{2} x d x+\tan x \sec ^{2} y d y=0$ is
(a) $\tan x+\tan y=k$
(b) $\tan x-\tan y=k$
(c) $\frac{\tan x}{\tan y}=k$
(d) $\tan x \cdot \tan y=k$
Show Answer
Solution
The given differential equation is
$ \tan y \sec ^{2} x d x+\tan x \sec ^{2} y d y=0 $
$\Rightarrow \tan x \sec ^{2} y d y=-\tan y \sec ^{2} x d x$
$\Rightarrow \quad \frac{\sec ^{2} y}{\tan y} \cdot d y=\frac{-\sec ^{2} x}{\tan x} \cdot d x$
Integrating both sides, we get
$ \begin{aligned} & \Rightarrow \quad \int \frac{\sec ^{2} y}{\tan y} d y=\int \frac{-\sec ^{2} x}{\tan x} d x \\ & \Rightarrow \quad \log |\tan y|=-\log |\tan x|+\log |c| \\ & \Rightarrow \quad \log |\tan y|+\log |\tan x|=\log |c| \\ & \Rightarrow \quad \log |\tan x. \tan y|=\log |c| \\ & \Rightarrow \quad |\tan x. \tan y|= |c| \\ & \Rightarrow \quad \tan x. \tan y= \pm c \\ & \Rightarrow \quad \tan x. \tan y= k \quad (where \quad k = \pm c) \end{aligned} $
Hence, option (d) is correct.
42. Family $y=A x+A^{3}$ of curves is represented by the differential equation of degree
(a) 1
(b) 2
(c) 3
(d) 4
Show Answer
Solution
The given equation is
$$ \begin{equation*} y=A x+A^{3}\tag{1} \end{equation*} $$
Differentiating both sides, we get $\frac{d y}{d x}=A$
put the value of A in equation 1
$y=x \frac{dy}{dx}+ (\frac {dy}{dx})^{3}$
So the degree of the differential equation is 3 .
Hence, the correct answer is (c).
43. Integrating factor of $x \frac{d y}{d x}-y=x^{4}-3x$ is
(a) $x$
(c) $\frac{1}{x}$
(b) $\log x$
(d) $-x$
Show Answer
Solution
The given differential equation is
$ x \frac{d y}{d x}-y=x^{4}-3 x \Rightarrow \frac{d y}{d x}-\frac{y}{x}=x^{3}-3 $
Here, $P=-\frac{1}{x}$ and $Q=x^{3}-3$
So, integrating factor $=e^{\int P d x}=e^{\int-\frac{1}{x} d x}=e^{-\log| x|}=e^{\log \frac{1}{x}}=\frac{1}{x} , (x>0) $
Hence, the correct option is (c).
44. Solution of $\frac{d y}{d x}-y=1, y(0)=1$ is given by
(a) $x y=-e^{x}$
(b) $x y=-e^{-x}$
(c) $x y=-1$
(d) $y=2 e^{x}-1$
Show Answer
Solution
The given differential equation is
$ \frac{d y}{d x}-y=1 $
Here, $P=-1, Q=1$
$\therefore$ Integrating factor, I.F. $=e^{\int P d x}=e^{\int-1 d x}=e^{-x}$
So, the solution is
$ \begin{aligned} & y \times \text{ I.F. }=\int Q \times \text{ I.F. } d x+c \\ & \Rightarrow \quad y \times e^{-x}=\int 1 . e^{-x} d x+c \\ & \Rightarrow \quad y \cdot e^{-x}=-e^{-x}+c \\ & \text{ Put } x=0, y=1 \\ & \Rightarrow \quad 1 \cdot e^{0}=-e^{0}+c \\ & \Rightarrow \quad 1=-1+c \quad \\ & \therefore c=2 \end{aligned} $
So the equation is $y \cdot e^{-x}=-e^{-x}+2$
$ \Rightarrow \quad y=-1+2 e^{x}=2 e^{x}-1 $
Hence, the correct option is $(d)$.
45. The number of solutions of $\frac{d y}{d x}=\frac{y+1}{x-1}$ when $y(1)=2$ is
(a) none
(b) one
(c) two
(d) infinite
Show Answer
Solution
The given differential equation is $\frac{d y}{d x}=\frac{y+1}{x-1}$
$ \Rightarrow \quad \frac{d y}{y+1}=\frac{d x}{x-1} $
Integrating both sides, we get
$\int \frac{d y}{y+1}=\int \frac{d x}{x-1}$
$\Rightarrow \log |(y+1)|=\log |(x-1)|+\log |c| $
$\Rightarrow \quad \log |(y+1)|-\log |(x-1)|=\log |c|$
$\Rightarrow \log |\frac{y+1}{x-1}|=\log |c| $
$\Rightarrow \frac{y+1}{x-1}=C \text{ Put } x=1 \text{ and } y=2 \quad where \quad C = \pm c$
$\Rightarrow \frac{2+1}{1-1}=C \quad \therefore C=\infty$
$\therefore \frac{y+1}{x-1}=\frac{1}{0} \Rightarrow x-1=0 \Rightarrow x=1$
Hence, the correct option is $(b)$.
46. Which of the following is a second order differential equation?
(a) $(y^{\prime})^{2}+x=y^{2}$
(c) $y^{ \prime}+(y^{ \prime})^{2}+y=0$
(b) $y^{\prime} y^{\prime \prime}+y=\sin x$
(d) $y^{\prime}=y^{2}$
Show Answer
Solution
Second order differential equation is $y^{\prime} y^{\prime \prime}+y=\sin x$
Hence, the correct option is $(b)$.
47. Integrating factor of the differential equation
$ (1-x^{2}) \frac{d y}{d x}-x y=1 \text{ is } $
(a) $-x$
(b) $\frac{x}{1+x^{2}}$
(c) $\sqrt{1-x^{2}}$
(d) $\frac{1}{2} \log (1-x^{2})$
Show Answer
Solution
The given differential equation is
$ \begin{aligned} & (1-x^{2}) \frac{d y}{d x}-x y=1 \\ \Rightarrow \quad & \frac{d y}{d x}-\frac{x}{1-x^{2}} \cdot y=\frac{1}{1-x^{2}} \end{aligned} $
Here, $P=-\frac{x}{1-x^{2}}$ and $Q=\frac{1}{1-x^{2}}$
$\therefore$ Integrating factor
$ \text{ I.F. }=e^{\int P d x}=e^{\int \frac{-x}{1-x^{2}} d x}=e^{\frac{1}{2} \log |(1-x^{2})|}=\sqrt{1-x^{2}}, \quad ( (1-x^{2})>0) $
Hence, the correct option is (c).
48. $\tan ^{-1} x+\tan ^{-1} y=c$ is the general solution of the differential equation:
(a) $\frac{d y}{d x}=\frac{1+y^{2}}{1+x^{2}}$
(b) $\frac{d y}{d x}=\frac{1+x^{2}}{1+y^{2}}$
(c) $(1+x^{2}) d y+(1+y^{2}) d x=0$
(d) $(1+x^{2}) d x+(1+y^{2}) d y=0$
Show Answer
Solution
Given equation is $\tan ^{-1} x+\tan ^{-1} y=c$
Differentiating w.r.t. $x$, we have
$ \begin{aligned} \frac{1}{1+x^{2}}+\frac{1}{1+y^{2}} \cdot \frac{d y}{d x} & =0 \\ \Rightarrow \quad(\frac{1}{1+y^{2}}) \frac{d y}{d x}=-(\frac{1}{1+x^{2}}) & \Rightarrow \frac{d y}{d x}=-(\frac{1+y^{2}}{1+x^{2}}) \\ \Rightarrow \quad(1+x^{2}) d y & =-(1+y^{2}) d x \\ \Rightarrow \quad(1+x^{2}) d y+(1+y^{2}) d x & =0 \end{aligned} $
Hence the correct option is (c).
49. The differential equation $y \frac{d y}{d x}+x=c$ represents:
(a) Family of hyperbolas
(c) Family of ellipses
(b) Family of parabolas
(d) Family of circles
Show Answer
Solution
Given differential equation is
$ \begin{aligned} y \frac{d y}{d x}+x & =c \\ \Rightarrow \quad y \frac{d y}{d x} & =c-x \quad \Rightarrow y d y=(c-x) d x \end{aligned} $
$\therefore$ Integrating both sides, we get
$\int y d y =\int(c-x) d x$
$\Rightarrow \frac{y^{2}}{2} =c x-\frac{x^{2}}{2}+k\Rightarrow \frac{x^{2}}{2}+\frac{y^{2}}{2}-c x=k$
$\Rightarrow x^{2}+y^{2}-2 c x =2 k \text{ which is a family of circles. }$
Hence, the correct option is (d).
50. The general solution of $e^{x} \cos y d x-e^{x} \sin y d y=0$ is:
(a) $e^{x} \cos y=k$
(b) $e^{x} \sin y=k$
(c) $e^{x}=k \cos y$
(d) $e^{x}=k \sin y$
Show Answer
Solution
The given differential equation is
$ e^{x} \cos y d x-e^{x} \sin y d y=0 $
$\Rightarrow e^{x}(\cos y d x-\sin y d y)=0$
$\Rightarrow \quad \cos y d x-\sin y d y=0$
$\Rightarrow \quad \sin y d y=\cos y d x \Rightarrow \frac{\sin y}{\cos y} d y=d x$
Integrating both sides, we have
$ \begin{aligned} \int \frac{\sin y}{\cos y} d y & =\int d x \\ \Rightarrow \quad-\log |\cos y| & =x+\log k \Rightarrow \log |\frac{1}{\cos y}|-\log k=x \\ \Rightarrow \quad \log (\frac{1}{k |\cos y|}) & =x \Rightarrow \frac{1}{k |\cos y|}=e^{x} \\ \Rightarrow \quad \frac{1}{k} & =e^{x} |\cos y| \Rightarrow e^{x} \cos y= \quad \pm \frac{1}{k} \\ &\Rightarrow e^{x} \cos y= c, \quad (where \quad c = \pm \frac {1}{k} ) \end{aligned} $
Hence, the correct option is (a).
51. The degree of the differential equation:
$ \frac{d^{2} y}{d x^{2}}+(\frac{d y}{d x})^{3}+6 y^{5}=0 \text{ is } $
(a) 1
(b) 2
(c) 3
(d) 5
Show Answer
Solution
The degree of the given differential equation is 1 as the power of the highest order is 1.
Hence, the correct option is $(a)$.
52. The solution of the differential equation
$ \frac{d y}{d x}+y=e^{-x}, y(0)=0 \text{ is } $
(a) $y=e^{x}(x-1)$
(c) $y=x e^{-x}+1$
(b) $y=x e^{-x}$
(d) $y=(x+1) e^{-x}$
Show Answer
Solution
The given differential equation is
$ \frac{d y}{d x}+y=e^{-x} $
Since, it is a linear differential equation of first order.
$\therefore P=1$ and $Q=e^{-x}$
$\therefore$ I.F $=e^{\int 1 . d x}=e^{x}$
So, the solution is
$ \begin{aligned} & \quad y \times \text{ I.F. }= \int Q \times \cdot \text{ I.F. } d x+c \Rightarrow y \cdot e^{x}=\int e^{-x} \cdot e^{x} d x+c \\ & \Rightarrow \quad y \cdot e^{x}=\int 1 \cdot d x+c \Rightarrow y \cdot e^{x}=x+c \\ & \text{ Put } x=0, y=0, \text{ we have } 0=0+c \quad \\ & \therefore c=0 \end{aligned} $
So, the solution is $y e^{x}=x \Rightarrow y=x \cdot e^{-x}$
Hence, the correct option is (b).
53. Integrating factor of the differential equation
$ \frac{d y}{d x}+y \tan x-\sec x=0 \text{ is } $
(a) $\cos x$
(b) $\sec x$
(c) $e^{\cos x}$
(d) $e^{\sec x}$
Show Answer
Solution
Given differential equation is
$ \frac{d y}{d x}+y \tan x-\sec x=0 \Rightarrow \frac{d y}{d x}+y \tan x=\sec x $
Here, $P=\tan x$ and $Q=\sec x$
$\therefore$ I.F. $=e^{\int P d x}=e^{\int \tan x d x}=e^{\log |\sec x|}=\sec x , (\sec x>0)$
Hence, the correct option is (b).
54. The solution of the differential equation
$ \frac{d y}{d x}=\frac{1+y^{2}}{1+x^{2}} \text{ is } $
(a) $y=\tan ^{-1} x$
(b) $y-x=k(1+x y)$
(c) $x=\tan ^{-1} y$
(d) $\tan (x y)=k$
Show Answer
Solution
The given differential equation is
$ \frac{d y}{d x}=\frac{1+y^{2}}{1+x^{2}} \Rightarrow \frac{d y}{1+y^{2}}=\frac{d x}{1+x^{2}} $
Integrating both sides, we get
$\int \frac{d y}{1+y^{2}} =\int \frac{d x}{1+x^{2}}$
$\Rightarrow \tan ^{-1} y =\tan ^{-1} x+c \Rightarrow \tan ^{-1} y-\tan ^{-1} x=c$
$\Rightarrow \tan^{-1}(\frac{y-x}{1+x y}) =c$
$\Rightarrow \frac{y-x}{1+x y} =\tan c \Rightarrow \frac{y-x}{1+x y}=k \quad[k=\tan c]$
$\Rightarrow y-x =k(1+x y)$
Hence, the correct option is $(b)$.
55. The integrating factor of the differential equation
$ \frac{d y}{d x}+y=\frac{1+y}{x} \text{ is: } $
(a) $\frac{x}{e^{x}}$
(b) $\frac{e^{x}}{x}$
(c) $x e^{x}$
(d) $e^{x}$
Show Answer
Solution
The given differential equation is
$ \frac{d y}{d x}+y=\frac{1+y}{x} $
$\begin{matrix} \Rightarrow & \frac{d y}{d x}=\frac{1+y}{x}-y \\ \Rightarrow & \frac{d y}{d x}=\frac{1}{x}+y \frac{(1-x)}{x} \Rightarrow \frac{d y}{d x}-(\frac{1-x}{x}) y=\frac{1}{x}\end{matrix} $
Here, $P=-(\frac{1-x}{x})$ and $Q=\frac{1}{x}$
$\therefore$ Integrating factor I.F. $=e^{\int P d x}=e^{\int \frac{x-1}{x} d x}=e^{\int(1-\frac{1}{x}) d x}$
$ =e^{(x-\log |x|)}=e^{x} \cdot e^{-\log x}, (x>0) $
$ =e^{x} \cdot e^{\log \frac{1}{x}}=e^{x} \cdot \frac{1}{x} $
Hence, the correct option is $(b)$.
56. $y=a e^{m x}+b e^{-m x}$ satisfies which of the following differential equations?
(a) $\frac{d y}{d x}+m y=0$
(b) $\frac{d y}{d x}-m y=0$
(c) $\frac{d^{2} y}{d x^{2}}-m^{2} y=0$
(d) $\frac{d^{2} y}{d x^{2}}+m^{2} y=0$
Show Answer
Solution
The given equation is $y=a e^{m x}+b e^{-m x}$
On differentiation, we get $\frac{d y}{d x}=a \cdot m e^{m x}-b \cdot m e^{-m x}$
Again differentiating w.r.t., we have
$ \begin{aligned} & \frac{d^{2} y}{d x^{2}}=a m^{2} e^{m x}+b m^{2} e^{-m x} \\ \Rightarrow & \frac{d^{2} y}{d x^{2}}=m^{2}(a e^{m x}+b e^{-m x}) \Rightarrow \frac{d^{2} y}{d x^{2}}=m^{2} y \Rightarrow \frac{d^{2} y}{d x^{2}}-m^{2} y=0 \end{aligned} $
Hence, the correct option is (c).
57. The solution of the differential equation $\cos x \sin y d x+\sin x \cos y d y=0$ is
(a) $\frac{\sin x}{\sin y}=c$
(b) $\sin x \sin y=c$
(c) $\sin x+\sin y=c$
(d) $\cos x \cos y=c$
Show Answer
Solution
The given differential equation is $\cos x \sin y d x+\sin x \cos y d y=0$
$\Rightarrow \quad \sin x \cos y d y=-\cos x \sin y d x$
$\Rightarrow \frac{\cos y}{\sin y} d y=-\frac{\cos x}{\sin x} d x \Rightarrow \cot y d y=-\cot x d x$
Integrating both sides, we have
$\Rightarrow \quad \int \cot y d y=-\int \cot x d x$
$ \begin{aligned} & \Rightarrow \quad \log |\sin y|=-\log |\sin x|+\log |C| \\ & \Rightarrow \quad \log |\sin y|+\log |\sin x|=\log |C| \\ & \Rightarrow \quad \log |\sin y \cdot \sin x|=\log |C| \Rightarrow \sin x \sin y=\pm C \\ & \Rightarrow \sin x \sin y=c, \quad (where \quad c= \pm C) \end{aligned} $
Hence, the correct option is (b).
58. The solution of $x \frac{d y}{d x}+y=e^{x}$ is:
(a) $y=\frac{e^{x}}{x}+\frac{k}{x}$
(b) $y=x e^{x}+c x$
(c) $y=x \cdot e^{x}+k$
(d) $x=\frac{e^{y}}{y}+\frac{k}{y}$
Show Answer
Solution
The given differential equation is $x \frac{d y}{d x}+y=e^{x}$
$\Rightarrow \quad \frac{d y}{d x}+\frac{y}{x}=\frac{e^{x}}{x}$
Here $P=\frac{1}{x}$ and $Q=\frac{e^{x}}{x}$
$\therefore$ Integrating factor I.F. $=e^{\int \frac{1}{x} d x}=e^{\log |x|}=x, (x>0)$
So, the solution is
$ \begin{aligned} y \times \text{ I.F. } & =\int Q \times \text{ I.F. } d x+k \Rightarrow y \times x=\int \frac{e^{x}}{x} \times x d x+k \\ \Rightarrow y \times x & =\int e^{x} d x+k \Rightarrow y \times x=e^{x}+k \\ \therefore y & =\frac{e^{x}}{x}+\frac{k}{x} \end{aligned} $
Hence, the correct option is $(a)$.
59. The differential equation of the family of curves $x^{2}+y^{2}-2 a y=0$, where $a$ is arbitrary constant, is:
(a) $(x^{2}-y^{2}) \frac{d y}{d x}=2 x y$
(b) $2(x^{2}+y^{2}) \frac{d y}{d x}=x y$
(c) $2(x^{2}-y^{2}) \frac{d y}{d x}=x y$
(d) $(x^{2}+y^{2}) \frac{d y}{d x}=2 x y$
Show Answer
Solution
The given equation is
$$ \begin{equation*} x^{2}+y^{2}-2 a y=0 \tag{1} \end{equation*} $$
Differentiating w.r.t. $x$, we have
$ \begin{aligned} & 2 x+2 y \cdot \frac{d y}{d x}-2 a \frac{d y}{d x}=0 \\ & \Rightarrow \quad x+y \frac{d y}{d x}-a \frac{d y}{d x}=0 \quad \Rightarrow \quad x+(y-a) \frac{d y}{d x}=0 \\ & \Rightarrow \quad(y-a) \frac{d y}{d x}=-x \quad \Rightarrow y-a=\frac{-x}{d y / d x} \end{aligned} $
$\Rightarrow \quad a=y+\frac{x}{d y / d x} \Rightarrow a=\frac{y \cdot \frac{d y}{d x}+x}{\frac{d y}{d x}}$
Putting the value of $a$ in eq. (1) we get
$ \begin{aligned} & x^{2}+y^{2}-2 y[\frac{y \frac{d y}{d x}+x}{\frac{d y}{d x}}]=0 \\ & \Rightarrow \quad(x^{2}+y^{2}) \frac{d y}{d x}-2 y(y \frac{d y}{d x}+x)=0 \\ & \Rightarrow \quad(x^{2}+y^{2}) \frac{d y}{d x}-2 y^{2} \frac{d y}{d x}-2 x y=0 \\ & \Rightarrow \quad(x^{2}+y^{2}-2 y^{2}) \frac{d y}{d x}=2 x y \Rightarrow(x^{2}-y^{2}) \frac{d y}{d x}=2 x y \end{aligned} $
$\therefore$ Hence the correct option is $(a)$.
60. Family $y=A x+A^{3}$ of curves will correspond to a differential equation of order
(a) 3
(b) 2
(c) 1
(d) not defined
Show Answer
Solution
The given equation is
$$ \begin{equation*} y=A x+A^{3}\tag{1} \end{equation*} $$
Differentiating both sides, we get $\frac{d y}{d x}=A$
put the value of A in equation 1
$y=x \frac{dy}{dx}+ (\frac {dy}{dx})^{3}$
So the order of the differential equation is 1 .
Hence, the correct option is $(c)$.
61. The general solution of $\frac{d y}{d x}=2 x e^{x^{2}-y}$ is :
(a) $e^{x^{2}-y}=c$
(c) $e^{y}=e^{x^{2}}+c$
(b) $e^{-y}+e^{x^{2}}=c$
(d) $e^{x^{2}+y}=c$
Show Answer
Solution
The given differential equation is
$ \begin{aligned} \frac{d y}{d x} & =2 x \cdot e^{x^{2}-y} \\ \Rightarrow \quad \frac{d y}{d x} & =2 x \cdot e^{x^{2}} \cdot e^{-y} \Rightarrow \frac{d y}{e^{-y}}=2 x \cdot e^{x^{2}} d x \end{aligned} $
Integrating both sides, we have
$ \begin{aligned} \int \frac{d y}{e^{-y}}=\int 2 x \cdot e^{x^{2}} d x \Rightarrow & \int e^{y} d y=\int 2 x \cdot e^{x^{2}} d x \\ & \text{ Put in RHS } x^{2}=t \therefore 2 x d x=d t \end{aligned} $
$ \begin{aligned} \therefore \quad \int e^{y} d y & =\int e^{t} d t \\ \Rightarrow \quad e^{y} & =e^{t}+c \Rightarrow e^{y}=e^{x^{2}}+c \\ \Rightarrow \quad e^{y-x^{2}} = c \end{aligned} $
Hence, the correct option is (c).
62. The curve for which the slope of the tangent at any point is equal to the ratio of the abscissa to the ordinate of the point is:
(a) an ellipse
(b) parabola
(c) circle
(d) rectangular hyperbola
Show Answer
Solution
Since, the slope of the tangent to the curve $=x: y$
$ \therefore \quad \frac{d y}{d x}=\frac{x}{y} \Rightarrow y d y=x d x $
Integrating both sides, we get $\int y d y=\int x d x$
$ \begin{aligned} & \Rightarrow \quad \frac{y^{2}}{2}=\frac{x^{2}}{2}+c \Rightarrow y^{2}=x^{2}+2 c \\ & \Rightarrow \quad y^{2}-x^{2}=2 c=k \text{ which is rectangular hyperbola. } \end{aligned} $
Hence, the correct option is $(d)$.
63. The general solution of the differential equation $\frac{d y}{d x}=e^{\frac{x^{2}}{2}}+x y$ is:
(a) $y=c \cdot e^{\frac{-x^{2}}{2}}$
(c) $y=(x+c) \cdot e^{{x^{2}}}$
(b) $y=c \cdot e^{\frac{x^{2}}{2}}$
(d) $y=(c-x) e^{\frac{x^{2}}{2}}$
Show Answer
Solution
The given differential equation is
$ \frac{d y}{d x}=e^{\frac{x^{2}}{2}}+x y \Rightarrow \frac{d y}{d x}-x y=e^{\frac{x^{2}}{2}} $
Since it is linear differential equation where $P=-x$ and $Q=e^{\frac{x^{2}}{2}}$
$\therefore$ Integrating factor I.F. $=e^{\int P d x}=e^{\int-x d x}=e^{-\frac{x^{2}}{2}}$
So, the solution is
$ \begin{aligned} & y \times \text{ I.F. }=\int Q \times \text{ I.F. } d x+c \\ & \Rightarrow \quad y \times e^{-\frac{x^{2}}{2}}=\int e^{\frac{x^{2}}{2}} e^{-\frac{x^{2}}{2}} d x+c \\ & \Rightarrow \quad y \times e^{-\frac{x^{2}}{2}}=\int e^{0} d x+c \\ & \Rightarrow \quad y \times e^{-\frac{x^{2}}{2}}=\int 1 . d x+c \Rightarrow y \times e^{-\frac{x^{2}}{2}}=x+c \end{aligned} $
$ \therefore \quad y=(x+c) e^{\frac{x^{2}}{2}} $
Hence the correct option is $(c)$.
Take left hand side
$\frac{d y}{d x} = \frac{d ((c-x) e^{\frac{x^{2}}{2}})}{d x}$
$=(c-x)\cdot e^\frac {x^{2}}{2} \cdot \frac {2x}{2}+e^\frac {x^{2}}{2} (0-1) $
$=x((c-x)e^\frac {x^{2}}{2})-e^\frac {x^{2}}{2}$
$=xy-e^\frac {x^{2}}{2}$
$\therefore $ the left-hand side is not equal the right-hand side.
Hence the option (d) is incorrect.
64. The solution of the equation $(2 y-1) d x-(2 x+3) d y=0$ is
(a) $\frac{2 x-1}{2 y+3}=k$
(b) $\frac{2 y+1}{2 x-3}=k$
(c) $\frac{2 x+3}{2 y-1}=k$
(d) $\frac{2 x-1}{2 y-1}=k$
Show Answer
Solution
The given differential equation is
$ \begin{aligned} (2 y-1) d x-(2 x+3) d y & =0 \Rightarrow(2 x+3) d y=(2 y-1) d x \\ \Rightarrow \quad \frac{d y}{2 y-1} & =\frac{d x}{2 x+3} \end{aligned} $
Integrating both sides, we get
$ \begin{matrix} \int \frac{d y}{2 y-1} =\int \frac{d x}{2 x+3} \\ \Rightarrow \quad \frac{1}{2} \log |2 y-1| =\frac{1}{2} \log |2 x+3|+\log c \\ \Rightarrow \quad \log |2 y-1| =\log |2 x+3|+2 \log c \\ \Rightarrow \quad \log |2 y-1|-\log |2 x+3| =\log c^{2} \\ \Rightarrow \quad \log |\frac{2 y-1}{2 x+3}| =\log c^{2} \\ \Rightarrow \quad \frac{2 y-1}{2 x+3} = \pm c^{2}\\ \Rightarrow \quad \frac{2 y-1}{2 x+3} = C , \quad where \quad C = \pm c^2 \\ \Rightarrow \quad \frac{2 x+3}{2 y-1}=\frac{1}{C} \\ \Rightarrow \quad \frac{2 x+3}{2 y-1} =k \text{, where } k=\frac{1}{C} \end{matrix} $
Hence, the correct option is (c).
65. The differential equation for which $y=a \cos x+b \sin x$ is a solution, is:
(a) $\frac{d^{2} y}{d x^{2}}+y=0$
(b) $\frac{d^{2} y}{d x^{2}}-y=0$
(c) $\frac{d^{2} y}{d x^{2}}+(a+b) y=0$
(d) $\frac{d^{2} y}{d x^{2}}+(a-b) y=0$
Show Answer
Solution
The given equation is
$ \begin{gathered} y=a \cos x+b \sin x \\ \frac{d y}{d x}=-a \sin x+b \cos x \end{gathered} $
$ \begin{aligned} \frac{d^{2} y}{d x^{2}} & =-a \cos x-b \sin x \\ \Rightarrow \quad \frac{d^{2} y}{d x^{2}} & =-(a \cos x+b \sin x) \Rightarrow \frac{d^{2} y}{d x^{2}}=-y \Rightarrow \frac{d^{2} y}{d x^{2}}+y=0 \end{aligned} $
Hence, the correct option is $(a)$.
66. The solution of $\frac{d y}{d x}+y=e^{-x}, y(0)=0$ is:
(a) $y=e^{-x}(x-1)$
(b) $y=x \cdot e^{x}$
(c) $y=x e^{-x}+1$
(d) $y=x \cdot e^{-x}$
Show Answer
Solution
The given differential equation is $\frac{d y}{d x}+y=e^{-x}$
Since, it is a linear differential equation then $P=1$ and $Q=e^{-x}$
Integrating factor I.F. $=e^{\int P d x}=e^{\int 1 . d x}=e^{x}$
$\therefore$ Solution is
$ \begin{aligned} y \times \text{ I.F. } & =\int Q \times \text{ I.F. } d x+c \\ \Rightarrow \quad y \times e^{x} & =\int e^{-x} \times e^{x} d x+c \Rightarrow y \times e^{x}=\int e^{0} d x+c \\ \Rightarrow \quad y \times e^{x} & =\int 1 . d x+c \Rightarrow y \times e^{x}=x+c \end{aligned} $
Put $y=0$ and $x=0$
$\therefore \quad 0=0+c \quad $
$\therefore \quad c=0$
$\therefore$ equation is $y \times e^{x}=x$
So $\quad y=x \cdot e^{-x}$
Hence, the correct option is $(d)$.
67. The order and degree of the differential equation
$ [\frac{d^{3} y}{d x^{3}}]^{2}-3 \frac{d^{2} y}{d x^{2}}+2(\frac{d y}{d x})^{4}=y^{4} \text{ are } $
(a) 1,4
(b) 3,4
(c) 2,4
(d) 3,2
Show Answer
Solution
The given differential equation is
$ [\frac{d^{3} y}{d x^{3}}]^{2}-3 \frac{d^{2} y}{d x^{2}}+2(\frac{d y}{d x})^{4}=y^{4} $
Here the highest derivative is $\frac{d^{3} y}{d x^{3}}$.
$\therefore$ the order of the differential equation is 3 and since, the power of highest order is 2
$\therefore$ its degree is 2
Hence, the correct option is (d).
68. The order and degree of the differential equation
$[1+(\frac{d y}{d x})^{2}]=\frac{d^{2} y}{d x^{2}}$ are:
(a) $2, \frac{3}{2}$
(b) 2,3
(c) 2, 1
(d) 3, 4
Show Answer
Solution
The given differential equation is
$ [1+(\frac{d y}{d x})^{2}]=\frac{d^{2} y}{d x^{2}} $
Here, the highest derivative is 2 ,
$\therefore$ order $=2$
and the power of the highest derivative is 1
$\therefore$ degree $=1$
Hence, the correct option is (c).
69. The differential equation of the family of curves $y^{2}=4 a(x+a)$ is:
(a) $y^{2}=4 \frac{d y}{d x}(x+\frac{d y}{d x})$
(b) $2 y \cdot \frac{d y}{d x}=4 a$
(c) $y \cdot \frac{d^{2} y}{d x^{2}}+(\frac{d y}{d x})^{2}=0$
(d) $2 x \cdot \frac{d y}{d x}+y(\frac{d y}{d x})^{2}-y=0$
Show Answer
Solution
The given equation of family of curves is
$$ \begin{align*} & y^{2}=4 a(x+a) \\ \Rightarrow \quad & y^{2}=4 a x+4 a^{2} \tag{1} \end{align*} $$
Differentiating both sides, w.r.t. $x$, we get
$ \begin{aligned} 2 y \cdot \frac{d y}{d x} & =4 a \\ \Rightarrow \quad y \cdot \frac{d y}{d x} & =2 a \Rightarrow \frac{y}{2} \frac{d y}{d x}=a \end{aligned} $
Now, putting the value of $a$ in eq. (1) we get
$ \begin{aligned} y^{2} & =4 x(\frac{y}{2} \frac{d y}{d x})+4(\frac{y}{2} \cdot \frac{d y}{d x})^{2} \\ \Rightarrow \quad y^{2} & =2 x y \frac{d y}{d x}+y^{2}(\frac{d y}{d x})^{2} \Rightarrow y=2 x \frac{d y}{d x}+y(\frac{d y}{d x})^{2} \end{aligned} $
$ \Rightarrow \quad 2 x \cdot \frac{d y}{d x}+y \cdot(\frac{d y}{d x})^{2}-y=0 $
Hence, the correct option is (d).
70. Which of the following is the general solution of
$ \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+y=0 ? $
(a) $y=(A x+B) \cdot e^{x}$
(b) $y=(A x+B) e^{-x}$
(c) $y=A e^{x}+B e^{-x}$
(d) $y=A \cos x+B \sin x$
Show Answer
Solution
The given differential equation is
$ \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+y=0 $
Since the above equation is of second order and first degree
$\therefore \quad D^{2} y-2 D y+y=0$, where $D=\frac{d}{d x}$
$\Rightarrow(D^{2}-2 D+1) y=0$
$\therefore$ auxiliary equation is
$ m^{2}-2 m+1=0 \Rightarrow(m-1)^{2}=0 \Rightarrow m=1,1 $
If the roots of Auxiliary equation are real and equal say $(m)$ then $C F=(ax+b) \cdot e^{m x}$
$\therefore \quad C F=(A x+B) e^{x}$
So $y=(A x+B) \cdot e^{x}$
Hence, the correct option is $(a)$.
71. General solution of $\frac{d y}{d x}+y \tan x=\sec x$ is:
(a) $y \sec x=\tan x+c$
(b) $y \tan x=\sec x+c$
(c) $\tan x=y \tan x+c$
(d) $x \sec x=\tan y+c$
Show Answer
Solution
The given differential equation is $\frac{d y}{d x}+y \tan x=\sec x$
Since, it is a linear differential equation
$\therefore \quad P=\tan x$ and $Q=\sec x$
Integrating factor I.F. $=e^{\int P d x}=e^{\int \tan x d x}=e^{\log |\sec x|}=\sec x, (\sec x>0)$
$\therefore$ Solution is
$ \begin{aligned} y \times \text{ I.F. } & =\int Q \times \text{ I.F. } d x+c \\ \Rightarrow \quad y \times \sec x & =\int \sec x \cdot \sec x d x+c \\ \Rightarrow \quad y \sec x & =\int \sec ^{2} x d x+c \Rightarrow y \sec x=\tan x+c \\ \Rightarrow y \sec x=\tan x+c \end{aligned} $
Hence, the correct option is (a).
72. Solution of differential equation $\frac{d y}{d x}+\frac{y}{x}=\sin x$ is:
(a) $x(y+\cos x)=\sin x+c$
(b) $x(y-\cos x)=\sin x+c$
(c) $x y \cos x=\sin x+c$
(d) $x(y+\cos x)=\cos x+c$
Show Answer
Solution
The given differential equation is $\frac{d y}{d x}+\frac{y}{x}=\sin x$
Since, it is a linear differential equation
$\therefore \quad P=\frac{1}{x}$ and $Q=\sin x$
Integrating factor I.F. $=e^{\int \frac{1}{x} d x}=e^{\log |x|}=x , (x>0)$
$\therefore$ Solution is $y \times$ I.F. $=\int Q \times$ I.F. $d x+c$
$ \begin{matrix} y \times x =\int \sin x \cdot x d x+c \Rightarrow y \times x=\int x \sin x d x+c \\ y x =x \cdot \int \sin x d x-\int(D(x) \int \sin x d x) d x+c \\ \Rightarrow y x =x(-\cos x)-\int-\cos x d x \\ \Rightarrow y x=-x \cos x+\int \cos x d x \Rightarrow y x=-x \cos x+\sin x+c \\ \Rightarrow y x+x \cos x =\sin x+c \\ \Rightarrow x(y+\cos x) =\sin x+c \end{matrix} $
Hence, the correct option is $(a)$.
73. The general solution of the differential equation $(e^{x}+1) y d y=(y+1) e^{x} d x$ is:
(a) $(y+1)=k(e^{x}+1)$
(b) $y+1=e^{x}+1+k$
(c) $y=\log [k(y+1)(e^{x}+1)]$
(d) $y=\log {\frac{e^{x}+1}{y+1}}+k$
Show Answer
Solution
The given differential equation is
$ \begin{aligned} (e^{x}+1) y d y & =(y+1) e^{x} d x \\ \Rightarrow \quad \frac{y}{y+1} d y & =\frac{e^{x}}{e^{x}+1} d x \end{aligned} $
Integrating both sides, we get
$ \begin{aligned} \int \frac{y}{y+1} d y & =\int \frac{e^{x}}{e^{x}+1} d x \\ \Rightarrow \quad \int \frac{y+1-1}{y+1} d y & =\int \frac{e^{x}}{e^{x}+1} d x \\ \Rightarrow \quad \int 1 \cdot d y-\int \frac{1}{y+1} d y & =\int \frac{e^{x}}{e^{x}+1} d x \end{aligned} $
$ \begin{aligned} \Rightarrow \quad y-\log |y+1| =\log |e^{x}+1|+\log |c| \\ \Rightarrow \quad y =\log |y+1|+\log |e^{x}+1|+\log |c| \\ \Rightarrow \quad y =\log |c(y+1)(e^{x}+1)| \\ \Rightarrow \quad y =\log [k(y+1)(e^{x}+1)] , \quad (where \quad k= \pm c) \end{aligned} $
Hence, the correct option is (c).
74. The solution of differential equation $\frac{d y}{d x}=e^{x-y}+x^{2} e^{-y}$ is:
(a) $y=e^{x-y}-x^{2} e^{-y}+c$
(b) $e^{y}-e^{x}=\frac{x^{3}}{3}+c$
(c) $e^{x}+e^{y}=\frac{x^{3}}{3}+c$
(d) $e^{x}-e^{y}=\frac{x^{3}}{3}+c$
Show Answer
Solution
The given differential equation is
$ \begin{aligned} & \frac{d y}{d x}=e^{x-y}+x^{2} e^{-y} \\ & \Rightarrow \quad \frac{d y}{d x}=e^{x} \cdot e^{-y}+x^{2} \cdot e^{-y} \Rightarrow \frac{d y}{d x}=e^{-y}(e^{x}+x^{2}) \\ & \Rightarrow \quad \frac{d y}{e^{-y}}=(e^{x}+x^{2}) d x \Rightarrow e^{y} \cdot d y=(e^{x}+x^{2}) d x \end{aligned} $
Integrating both sides, we have
$ \begin{aligned} \int e^{y} d y & =\int(e^{x}+x^{2}) d x \\ \Rightarrow \quad e^{y} & =e^{x}+\frac{x^{3}}{3}+c \Rightarrow e^{y}-e^{x}=\frac{x^{3}}{3}+c \end{aligned} $
Hence, the correct option is $(b)$.
75. The solution of the differential equation
$ \frac{d y}{d x}+\frac{2 x y}{1+x^{2}}=\frac{1}{(1+x^{2})^{2}} \text{ is: } $
(a) $y(1+x^{2})=c+\tan ^{-1} x$
(b) $\frac{y}{1+x^{2}}=c+\tan ^{-1} x$
(c) $y \log (1+x^{2})=c+\tan ^{-1} x$
(d) $y(1+x^{2})=c+\sin ^{-1} x$
Show Answer
Solution
The given differential equation is
$ \frac{d y}{d x}+\frac{2 x y}{1+x^{2}}=\frac{1}{(1+x^{2})^{2}} $
Since, it is a linear differential equation
$ P=\frac{2 x}{1+x^{2}} \text{ and } Q=\frac{1}{(1+x^{2})^{2}} $
Integrating factor I.F. $=e^{\int P d x}=e^{\int \frac{2 x}{1+x^{2}} d x}=e^{\log |(1+x^{2})|}=|(1+x^{2})|=(1+x^{2}), \quad (\because (1+x^{2}) \quad is \quad positive) $
$\therefore$ Solution is $y \times$ I.F. $=\int Q \times$ I.F. $d x+c$
$ \begin{aligned} & \Rightarrow \quad y(1+x^{2})=\int \frac{1}{(1+x^{2})^{2}} \times(1+x^{2}) d x+c \\ & \Rightarrow \quad y(1+x^{2})=\int \frac{1}{(1+x^{2})} d x+c \Rightarrow y(1+x^{2})=\tan ^{-1} x+c \end{aligned} $
Hence, the correct option is $(a)$.
Fillers
76. Fill in the blanks of the following ( $i$ to $x i$ ):
(i) The degree of the differential equation $\frac{d^{2} y}{d x^{2}}+e^{d y / d x}=0$ is ……
(ii) The degree of the differential equation $\sqrt{1+(\frac{d y}{d x})^{2}}=x$ is ……
(iii) The number of arbitrary constants in the general solution of a differential equation of order three is ……
(iv) $\frac{d y}{d x}+\frac{y}{x \log x}=\frac{1}{x}$ is an equation of the type ……
(v) General solution of the differential equation of the type $\frac{d x}{d y}+P_1 x=Q_1$ is given by ……
(vi) The solution of the differential equation $x \frac{d y}{d x}+2 y=x^{2}$ is ……
(vii) The solution of $(1+x^{2}) \frac{d y}{d x}+2 x y-4 x^{2}=0$ is ……
(viii) The solution of the differential equation $y d x+(x+x y) d y=0$ is ……
(ix) General solution of $\frac{d y}{d x}+y=\sin x$ is ……
( $x$ ) The solution of differential equation $\cot y d x=x d y$ is ……
(xi) The integrating factor of $\frac{d y}{d x}+y=\frac{1+y}{x}$ is ……
Show Answer
Solution
(i) The degree of the differential equation $\frac{d^{2} y}{d x^{2}}+e^{d y / d x}=0$ is not defined.
(ii) The given differential equation is $\sqrt{1+(\frac{d y}{d x})^{2}}=x$ Squaring both sides, we get
$ 1+(\frac{d y}{d x})^{2}=x^{2} $
So, the degree of the equation is 2 .
(iii) The number of arbitrary constants in the solution is 3 .
(iv) The given differential equation $\frac{d y}{d x}+\frac{y}{x \log x}=\frac{1}{x}$ is of the type $\frac{d y}{d x}+P y=Q$.
(v) General solution of the differential equation of the type $\frac{d x}{d y}+P_1 x=Q_1$ is given by $x \times$ I.F. $=\int Q \times$ I.F. $d y+c$
$\Rightarrow \quad x \cdot e^{\int P_1 d y}=\int Q_1 \cdot e^{\int P_1 d y} d y+c$.
(vi) The given differential equation is $x \frac{d y}{d x}+2 y=x^{2}$
$\Rightarrow \quad \frac{d y}{d x}+\frac{2}{x} y=x$.
Since, it is linear differential equation
$\therefore \quad P=\frac{2}{x}$ and $Q=x$
Integrating factor I.F. $=e^{\int P d x}=e^{\int \frac{2}{x} d x}=e^{2 \log |x|}=e^{\log |x^{2}|}=x^{2}$
$\therefore$ Solution is
$ \begin{aligned} y \times \text{ I.F. } & =\int Q \times \text{ I.F. } d x+c \\ \Rightarrow \quad y \cdot x^{2} & =\int x \cdot x^{2} d x+c \quad \Rightarrow y \cdot x^{2}=\int x^{3} d x+c \\ \Rightarrow \quad y \cdot x^{2} & =\frac{1}{4} x^{4}+c \quad \Rightarrow y=\frac{1}{4} x^{2}+c \cdot x^{-2} \end{aligned} $
Hence, the solution is $y=\frac{1}{4} x^{2}+c \cdot x^{-2}$.
(vii) The given differential equation is
$ \begin{aligned} & (1+x^{2}) \frac{d y}{d x}+2 x y-4 x^{2}=0 \\ \Rightarrow \quad & \frac{d y}{d x}+\frac{2 x y}{1+x^{2}}=\frac{4 x^{2}}{1+x^{2}} \end{aligned} $
Since it is a linear differential equation
$\therefore \quad P=\frac{2 x}{1+x^{2}}$ and $Q=\frac{4 x^{2}}{1+x^{2}}$
Integrating factor I.F. $=e^{\int P d x}=e^{\int \frac{2 x}{1+x^{2}} d x}=e^{\log |(1+x^{2})|}=(1+x^{2}) , \quad (\because (1+x^{2}) \quad is \quad positive )$
$\therefore$ Solution is $y \times I$.F $=\int Q \times$ I.F. $d x+c$
$ \begin{aligned} \Rightarrow y \times(1+x^{2}) =\int \frac{4 x}{1+x^{2}} \times(1+x^{2}) d x+c \\ \Rightarrow y \times(1+x^{2}) =\int 4 x^{2} d x+c \Rightarrow y \times(1+x^{2})=\frac{4}{3} x^{3}+c \\ \Rightarrow y =\frac{4}{3} \frac{x^{3}}{(1+x^{2})}+c(1+x^{2})^{-1} \end{aligned} $
$\Rightarrow 3y (1+x^{2})= 4x^{3}+3c$
$\Rightarrow 3y (1+x^{2})= 4x^{3}+C , (where \quad C=3c)$
Hence, the required solution is $ 3y (1+x^{2})= 4x^{3}+C$
(viii) The given differential equation is
$ \begin{gathered} y d x+(x+x y) d y=0 \\ \Rightarrow \quad(x+x y) d y=-y d x \Rightarrow x(1+y) d y=-y d x \\ \Rightarrow \quad \frac{1+y}{y} d y=-\frac{1}{x} d x \end{gathered} $
Integrating both sides, we get
$ \begin{aligned} & \int \frac{1+y}{y} d y=-\int \frac{1}{x} d x \\ & \Rightarrow \quad \int(\frac{1}{y}+1) d y=-\int \frac{1}{x} d x \\ & \Rightarrow \quad \log |y|+y=-\log |x|+\log |c| \\ & \Rightarrow \log |x|+\log |y|=\log |c|-y \\ & \Rightarrow \quad \log |x y |=\log |c|-y \\ & \Rightarrow \quad |x y |=e^{\log|c|}e^{-y} \\ & \Rightarrow \quad x y =\pm e^{\log|c|}e^{-y} \\ & \Rightarrow \quad x y =Ce^{-y} , \quad (where \quad C=\pm e^{\log|c|} )\\ \end{aligned} $
Hence, the required solution is $x y=C e^{-y}$.
(ix) The given differential equation is $\frac{d y}{d x}+y=\sin x$
Since, it it a linear differential equation
$\therefore \quad P=1$ and $Q=\sin x$
Integrating factor I.F. $=e^{\int P d x}=e^{\int 1 . d x}=e^{x}$
$\therefore$ Solution is $y \times$ I.F. $=\int Q \times$ I.F. $d x+c$
$\Rightarrow \quad y \cdot e^{x}=\int \sin x \cdot e^{x} d x+c$
Let $ I=\int \sin x \cdot e^{x} d x$
$ Intigration \quad by \quad part $
$ \begin{aligned} & I=\sin x \cdot \int e^{x} d x-\int(D(\sin x) \cdot \int e^{x} d x) d x \\ & I=\sin x \cdot e^{x}-\int \cos x \cdot e^{x} d x \\ & I=\sin x \cdot e^{x}-[\cos x \cdot \int e^{x} d x-\int(D(\cos x) \int e^{x} d x) d x] \end{aligned} $
$ \begin{aligned} I & =\sin x \cdot e^{x}-[\cos x \cdot e^{x}-\int-\sin x \cdot e^{x} d x] \\ I & =\sin x \cdot e^{x}-\cos x \cdot e^{x}-\int \sin x \cdot e^{x} d x \\ I & =\sin x \cdot e^{x}-\cos x \cdot e^{x}-I \\ \Rightarrow I+I & =e^{x}(\sin x-\cos x) \\ \Rightarrow \quad 2 I & =e^{x}(\sin x-\cos x) \\ \therefore \quad I & =\frac{e^{x}}{2}(\sin x-\cos x) \end{aligned} $
From eq. (1) we get
$ \begin{aligned} y \cdot e^{x} & =\frac{e^{x}}{2}(\sin x-\cos x)+c \\ y & =(\frac{\sin x-\cos x}{2})+c \cdot e^{-x} \end{aligned} $
Hence, the required solution is
$ y=(\frac{\sin x-\cos x}{2})+c \cdot e^{-x} $
(x) The given differential equation is $\cot y d x=x d y$
$ \Rightarrow \frac{d y}{\cot y}=\frac{d x}{x} \Rightarrow \tan y d y=\frac{d x}{x} $
Integrating both sides, we get
$ \begin{aligned} & \quad \int \tan y d y=\int \frac{d x}{x} \Rightarrow \log |\sec y|=\log |x|+\log |c| \\ \Rightarrow \quad & \log |\sec y|-\log |x|=\log |c| \\ \Rightarrow \quad & \log |\frac{\sec y}{x}|=\log |c| \\ \therefore \quad & |\frac{\sec y}{x}|=|c| \\ \therefore \quad & \frac{\sec y}{x}=\pm c \\ \therefore \quad & \frac{\sec y}{x}=C \quad ( where \quad C = \pm c)\\ \Rightarrow & \frac{x}{\sec y}=\frac{1}{C} \Rightarrow \frac{x}{\sec y}=C \\ \therefore \quad & x=C \sec y \end{aligned} $
Hence, the required solution is $x=C \sec y$.
$(x i)$ The given differential equation is
$ \begin{aligned} \frac{d y}{d x}+y & =\frac{1+y}{x} \\ \frac{d y}{d x}+y & =\frac{1}{x}+\frac{y}{x} \\ \Rightarrow \quad \frac{d y}{d x}+y-\frac{y}{x} & =\frac{1}{x} \Rightarrow \frac{d y}{d x}+(1-\frac{1}{x}) y=\frac{1}{x} \end{aligned} $
$ \begin{aligned} & \text{ Here } P=(1-\frac{1}{x}) \\ & \therefore \quad \text{ I.F. }=e^{\int P d x}=e^{\int(1-\frac{1}{x}) d x}=e^{(x-\log |x|)} \\ & =e^{x} \cdot e^{-\log |x|}=e^{x} \cdot e^{\log |\frac{1}{x}|}=\frac{e^{x}}{|x|}=\frac{e^{x}}{x},(x>0) \end{aligned} $
Hence, the required I.F. $=\frac{e^{x}}{x}$
True/False
77. State True or False for the following:
(i) Integrating factor of the differential equation of the form $\frac{d x}{d y}+P_1 x=Q_1$ is given by $e^{\int P_1 d y}$.
(ii) Solution of the differential equation of the type $\frac{d x}{d y}+P_1 x=Q_1$ is given by $x$. I.F. $=\int$ (I.F.) $Q_1 d y$.
(iii) Correct substitution for the solution of the differential equation of the type $\frac{d y}{d x}=f(x, y)$, where $f(x, y)$ is a homogeneous function of zero degree is $y=v x$.
(iv) Correct substitution for the solution of the differential equation of the type $\frac{d x}{d y}=g(x, y)$, where $g(x, y)$ is a homogeneous function of the degree zero is $x=v y$.
(v) Number of arbitrary constants in the particular solution of a differential equation of order two is two.
(vi) The differential equation representing the family of circles $x^{2}+(y-a)^{2}=a^{2}$ will be of order two.
(vii) The solution of $\frac{d y}{d x}=(\frac{y}{x})^{1 / 3}$ is $y^{2 / 3}-x^{2 / 3}=c$.
(viii) Differential equation representing the family of curves
$ y=e^{x}(A \cos x+B \sin x) \text{ is } \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+2 y=0 . $
(ix) The solution of differential equation $\frac{d y}{d x}=\frac{x+2 y}{x}$ is $x+y=k x^{2}$.
(x) Solution of $\frac{x d y}{d x}=y+x \tan \frac{y}{x}$ is $\sin (\frac{y}{x})=c x$.
(xi) The differential equation of all non-horizontal lines in a plane is $\frac{d^{2} x}{d y^{2}}=0$.
Show Answer
Solution
(i) True
I.F. of the given differential equation
$ \frac{d x}{d y}+P_1 x=Q \text{ is } e^{\int P_1 d y} $
(ii) True
(iii) True
(iv) True
(v) False
Since particular solution of a differential equation has no arbitrary constant.
(vi) False
We know that the order of the differential equation is equal to the number of arbitrary constants.
(vii) True
The given differential equation is
$ \begin{aligned} \frac{d y}{d x} & =(\frac{y}{x})^{1 / 3} \\ \Rightarrow \quad \frac{d y}{d x} & =\frac{y^{1 / 3}}{x^{1 / 3}} \Rightarrow \frac{d y}{y^{1 / 3}}=\frac{d x}{x^{1 / 3}} \end{aligned} $
Integrating both sides, we get
$\int \frac{d y}{y^{1 / 3}} =\int \frac{d x}{x^{1 / 3}} \Rightarrow \int y^{-1 / 3} d y=\int x^{-1 / 3} d x$
$\Rightarrow \frac{1}{-\frac{1}{3}+1} y^{-1 / 3+1} =\frac{1}{-1 / 3+1} \cdot x^{-1 / 3+1}+c$
$\Rightarrow \quad \frac{3}{2} y^{2 / 3} =\frac{3}{2} x^{2 / 3}+c$
$\Rightarrow \quad y^{2 / 3} =x^{2 / 3}+\frac{2}{3} c \Rightarrow y^{2 / 3}-x^{2 / 3}=k[k=\frac{2}{3} c]$
(viii) True
Given equation is
$ y=e^{x}(A \cos x+B \sin x) $
Differentiating both sides, we get
$ \begin{aligned} & \frac{d y}{d x}=e^{x}(-A \sin x+B \cos x)+(A \cos x+B \sin x) e^{x} \\ & \frac{d y}{d x}=e^{x}(-A \sin x+B \cos x)+y \end{aligned} $
Again differentiating w.r.t. $x$, we get
$ \begin{aligned} & \frac{d^{2} y}{d x^{2}}=e^{x}(-A \cos x-B \sin x)+(-A \sin x+B \cos x) \cdot e^{x}+\frac{d y}{d x} \\ & \frac{d^{2} y}{d x^{2}}=-e^{x}(A \cos x+B \sin x)+\frac{d y}{d x}-y+\frac{d y}{d x} \\ & \frac{d^{2} y}{d x^{2}}=-y-y+2 \frac{d y}{d x} \quad \therefore \quad \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+2 y=0 \end{aligned} $
(ix) True
The given differential equation is
$ \begin{aligned} \frac{d y}{d x} & =\frac{x+2 y}{x} \\ \Rightarrow \quad \frac{d y}{d x} & =1+2 \frac{y}{x} \Rightarrow \frac{d y}{d x}-\frac{2 y}{x}=1 \end{aligned} $
Here, $P=\frac{-2}{x}$ and $Q=1$
Integrating factor I.F. $=e^{\int \frac{-2}{x} d x}=e^{-2 \log |x|}=e^{\log |x|^{-2}}=\frac{1}{|x|^{2}} = \frac{1}{x^{2}}$
$\therefore$ Solution is $y \times$ I.F. $=\int Q \times$ I.F. $d x+c$
$\Rightarrow y \times \frac{1}{x^{2}}=\int 1 \times \frac{1}{x^{2}} d x+c$
$\Rightarrow \quad \frac{y}{x^{2}}=\int \frac{1}{x^{2}} d x+c \Rightarrow \frac{y}{x^{2}}=-\frac{1}{x}+c$
$\Rightarrow \quad y=-x+c x^{2} \Rightarrow y+x=c x^{2}$
(x) True
The given differential equation is
$ \begin{aligned} & x \frac{d y}{d x}=y+x \tan (\frac{y}{x}) \\ & x \frac{d y}{d x}-x \tan (\frac{y}{x})=y \\ & \Rightarrow \frac{d y}{d x}-\tan (\frac{y}{x})=\frac{y}{x} \Rightarrow \frac{d y}{d x}=\frac{y}{x}+\tan (\frac{y}{x}) \\ & \text{ Put } y=v x \Rightarrow \frac{d y}{d x}=v+x \frac{d v}{d x} \\ & \Rightarrow \quad v+x \cdot \frac{d v}{d x}=\frac{v x}{x}+\tan (\frac{v x}{x}) \end{aligned} $
$ \begin{aligned} & \Rightarrow \quad v+x \frac{d v}{d x}=v+\tan v \Rightarrow x \frac{d v}{d x}=\tan v \\ & \Rightarrow \quad \frac{d v}{\tan v}=\frac{d x}{x} \Rightarrow \cot v d v=\frac{d x}{x} \end{aligned} $
Integrating both sides, we get
$ \begin{matrix} \int \cot v d v =\int \frac{d x}{x} \Rightarrow \log |\sin v|=\log |x|+\log |c| \\ \Rightarrow \log |\sin \frac{y}{x}|=\log |x c| \\ \therefore \qquad \sin \frac{y}{x} =\pm cx \\ \therefore \qquad \sin \frac{y}{x} =Cx , \quad (where \quad C= \pm c) \end{matrix} $
(xi) True
Let $y=m x+c$ be the non-horizontal line in a plane
$\therefore \qquad \frac{d y}{d x}=m$ and $\frac{d^{2} y}{d x^{2}}=0$.





