Solution

Let $\alpha=60^{\circ}, \beta=45^{\circ}$ and the angle inclined to OZ axis be $\gamma$

We know that

$\cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma=1$

$\Rightarrow \cos ^{2} 60^{\circ}+\cos ^{2} 45^{\circ}+\cos ^{2} \gamma=1$

$\Rightarrow \quad(\dfrac{1}{2})^{2}+(\dfrac{1}{\sqrt{2}})^{2}+\cos ^{2} \gamma=1 \quad \Rightarrow \quad \dfrac{1}{4}+\dfrac{1}{2}+\cos ^{2} \gamma=1$

$\Rightarrow \quad \dfrac{3}{4}+\cos ^{2}\gamma=1 \Rightarrow \cos ^{2} \gamma=1-\dfrac{3}{4}=\dfrac{1}{4}$

$\therefore \quad \cos \gamma= \pm \dfrac{1}{2}$

$\therefore \quad \overrightarrow{{}OA}=|\overrightarrow{{}OA}|(\dfrac{1}{2} \hat{i}+\dfrac{1}{\sqrt{2}} \hat{j}\pm\dfrac{1}{2} \hat{k})=10(\dfrac{1}{2} \hat{i}+\dfrac{1}{\sqrt{2}} \hat{j}\pm\dfrac{1}{2} \hat{k})$

$=5 \hat{i}+5 \sqrt{2} \hat{j}\pm5 \hat{k}$

Hence, the position vector of $A$ is $(5 \hat{i}+5 \sqrt{2} \hat{j}\pm5 \hat{k})$.

Solution

We know that the equation of line is

$ \vec{r}=\vec{a}+\vec{b} \lambda $

Here, $\vec{a}=\hat{i}-2 \hat{j}+3 \hat{k}$ and $ \overrightarrow{{}b}= 3\hat{i}-2 \hat{j}+6 \hat{k}$

$\therefore$ Equation of line is $\vec{r}=(\hat{i}-2 \hat{j}+3 \hat{k})+\lambda(3 \hat{i}-2 \hat{j}+6 \hat{k}) $

$\Rightarrow (x\hat{i} + y \hat{j}+ z \hat{k})= (\hat{i}-2 \hat{j}+3 \hat{k})+\lambda(3 \hat{i}-2 \hat{j}+6 \hat{k})$

$\Rightarrow(x \hat{i}+y \hat{j}+z \hat{k})-(\hat{i}-2 \hat{j}+3 \hat{k})=\lambda(3 \hat{i}-2 \hat{j}+6 \hat{k})$

$\Rightarrow(x-1) \hat{i}+(y+2) \hat{j}+(z-3) \hat{k}=\lambda(3 \hat{i}-2 \hat{j}+6 \hat{k})$

Hence, the required equation is

$(x-1) \hat{i}+(y+2) \hat{j}+(z-3) \hat{k}=\lambda(3 \hat{i}-2 \hat{j}+6 \hat{k})$

Solution

The given equations are

$ \begin{aligned} & \dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4} \text{ and } \dfrac{x-4}{5}=\dfrac{y-1}{2}=z \\ & \text{ Let } \quad \dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}=\lambda \\ & \therefore x=2 \lambda+1, y=3 \lambda+2 \text{ and } z=4 \lambda+3 \\ & \text{ and } \quad \dfrac{x-4}{5}=\dfrac{y-1}{2}=\dfrac{z}{1}=\mu \\ & \therefore x=5 \mu+4, y=2 \mu+1 \text{ and } z=\mu \end{aligned} $

If the two lines intersect each other at one point,

then $2 \lambda+1=5 \mu+4 \Rightarrow 2 \lambda-5 \mu=3\quad …$ (i)

$3 \lambda +2=2 \mu+1 \Rightarrow 3 \lambda-2 \mu=-1 \quad …$ (ii)

and $4 \lambda+3=\mu \quad \Rightarrow 4 \lambda-\mu=-3 \quad …$ (iii)

Solving eqns. (i) and (ii) we get

$\begin{aligned} \Rightarrow 6 \lambda-15 \mu=9 \\ 6 \lambda-4 \mu=-2 \\ (-) \quad (+) \quad (+) \\ \hline \quad -11 \mu =\quad 11 \\ \therefore \quad \mu=-1 \end{aligned}$

Putting the value of $\mu$ in eq. (i) we get,

$2\lambda -5(-1) =3$

$\Rightarrow \quad 2 \lambda+5 =3$

$\Rightarrow \quad 2 \lambda =-2 \quad \therefore \lambda=-1$

Now putting the value of $\lambda$ and $\mu$ in eq. (iii) then

$ \begin{aligned} 4(-1)-(-1) & =-3 \\ -4+1 & =-3 \\ -3 & =-3 \text{ (satisfied) } \end{aligned} $

$\therefore$ Given lines intersect and coordinates of the point of intersection are

$ \begin{aligned} & x=5(-1)+4=-5+4=-1 \\ & y=2(-1)+1=-2+1=-1 \\ & z=-1 \end{aligned} $

Hence, the given lines intersect each other at $(-1,-1,-1)$.

Solution

Here,

$ \vec{b} _1=2 \hat{i}+\hat{j}+2 \hat{k} \text{ and } \vec{b} _2=6 \hat{i}+3 \hat{j}+2 \hat{k} $

$ \begin{aligned} \therefore \quad \cos \theta & =\dfrac{ \vec{b} _1 \cdot \vec{b} _2}{| \vec{b} _1| \vec{b} _2 \mid}=\dfrac{(2 \hat{i}+\hat{j}+2 \hat{k}) \cdot(6 \hat{i}+3 \hat{j}+2 \hat{k})}{\sqrt{(2)^{2}+(1)^{2}+(2)^{2}} \cdot \sqrt{(6)^{2}+(3)^{2}+(2)^{2}}} \\ & =\dfrac{12+3+4}{\sqrt{4+1+4} \cdot \sqrt{36+9+4}}=\dfrac{19}{\sqrt{9} \cdot \sqrt{49}}=\dfrac{19}{3 \cdot 7}=\dfrac{19}{21} \\ \therefore \quad \theta & =\cos ^{-1}(\dfrac{19}{21}) \end{aligned} $

Hence, the required angle is $\cos ^{-1}(\dfrac{19}{21})$.

Solution

Given points are $A(0,-1,-1)$ , $B(4,5,1)$, $C(3,9,4) \text{ and } D(-4,4,4)$

Cartesian form of equation $AB$ is

$ \dfrac{x-0}{4-0}=\dfrac{y+1}{5+1}=\dfrac{z+1}{1+1} \Rightarrow \dfrac{x}{4}=\dfrac{y+1}{6}=\dfrac{z+1}{2} $

and its vector form is $\vec{r}=(-\hat{j}-\hat{k})+\lambda(4 \hat{i}+6 \hat{j}+2 \hat{k})$

Similarly, equation of $CD$ is

$ \dfrac{x-3}{-4-3}=\dfrac{y-9}{4-9}=\dfrac{z-4}{4-4} \Rightarrow \dfrac{x-3}{-7}=\dfrac{y-9}{-5}=\dfrac{z-4}{0} $

and its vector form is $\vec{r}=(3 \hat{i}+9 \hat{j}+4 \hat{k})+\mu(-7 \hat{i}-5 \hat{j})$

Now, here $ \vec{a} _1=-\hat{j}-\hat{k}, \quad \vec{b} _1=4 \hat{i}+6 \hat{j}+2 \hat{k}$

$ \vec{a} _2=3 \hat{i}+9 \hat{j}+4 \hat{k}, \quad \vec{b} _2=-7 \hat{i}-5 \hat{j} $

Shortest distance between $AB$ and $CD$

$ \begin{aligned} \text{ S.D. } & =|\dfrac{( \vec{a} _2- \vec{a} _1) \cdot( \vec{b} _1 \times \vec{b} _2)}{| \vec{b} _1 \times \vec{b} _2|}| \\ \vec{a} _2- \vec{a} _1 & =(3 \hat{i}+9 \hat{j}+4 \hat{k})-(-\hat{j}-\hat{k})=3 \hat{i}+10 \hat{j}+5 \hat{k} . \\ \vec{b} _1 \times \vec{b} _2 & = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 4 & 6 & 2 \\ -7 & -5 & 0 \end{vmatrix} \\ & =\hat{i}(0+10)-\hat{j}(0+14)+\hat{k}(-20+42) \\ & =10 \hat{i}-14 \hat{j}+22 \hat{k} \end{aligned} $

$ \begin{aligned} | \vec{b} _1 \times \vec{b} _2| & =\sqrt{(10)^{2}+(-14)^{2}+(22)^{2}} \\ & =\sqrt{100+196+484}=\sqrt{780} \\ \therefore \quad \quad \text{ S.D } & =\dfrac{(3 \hat{i}+10 \hat{j}+5 \hat{k}) \cdot(10 \hat{i}-14 \hat{j}+22 \hat{k})}{\sqrt{780}} \\ & =\dfrac{30-140+110}{\sqrt{780}}=0 \end{aligned} $

Hence, the two lines intersect each other.

Solution

Given that: $\quad x=p y+q \Rightarrow y=\dfrac{x-q}{p}$

and $ z=r y+s \Rightarrow y=\dfrac{z-s}{r} $

$\therefore$ The equation becomes

$\dfrac{x-q}{p}=\dfrac{y}{1}=\dfrac{z-s}{r}$ in which direction ratios are $a_1=p, b_1=1, c_1=r$

Similarly

$ x=p^{\prime} y+q^{\prime} \Rightarrow y=\dfrac{x-q^{\prime}}{p^{\prime}} $

and $ z=r^{\prime} y+s^{\prime} \Rightarrow y=\dfrac{z-s^{\prime}}{r^{\prime}} $

$\therefore$ The equation becomes

$ \dfrac{x-q^{\prime}}{p^{\prime}}=\dfrac{y}{1}=\dfrac{z-s^{\prime}}{r^{\prime}} \text{ in which } a_2=p^{\prime}, b_2=1, c_2=r^{\prime} $

If the lines are perpendicular to each other, then

$ \begin{matrix} a_1 a_2+b_1 b_2+c_1 c_2=0 \\ p p^{\prime}+1.1+r r^{\prime}=0 \end{matrix} $

Hence, $p p^{\prime}+r r^{\prime}+1=0$ is the required condition.

Solution

Given that $A(2,3,4)$ and $B(4,5,8)$

Coordinates of mid-point $C$ are $(\dfrac{2+4}{2}, \dfrac{3+5}{2}, \dfrac{4+8}{2})=(3,4,6)$

Now direction ratios of the normal to the plane

$ \begin{aligned} & =\text{ direction ratios of } AB \\ & =4-2,5-3,8-4=(2,2,4) \end{aligned} $

Equation of the plane is

$a(x-x_1)+b(y-y_1)+c(z-z_1) =0 $

$\Rightarrow \quad 2(x-3)+2(y-4)+4(z-6) =0 $

$\Rightarrow \quad 2 x-6+2 y-8+4 z-24 =0$

$\Rightarrow \quad 2 x+2 y+4 z =38 \quad \Rightarrow \quad x+y+2 z=19$

Hence, the required equation of plane is $x+y+2 z=19 \quad$ or $\quad \vec{r}(\hat{i}+\hat{j}+2 \hat{k})=19$.

Solution

Since, the normal to the plane is equally inclined to the axes

$\therefore \cos \alpha=\cos \beta=\cos \gamma$

$\Rightarrow \cos ^{2} \alpha+\cos ^{2} \alpha+\cos ^{2} \alpha=1$

$\begin{aligned} \Rightarrow 3 \cos ^{2} \alpha =1 \Rightarrow \cos \alpha=\dfrac{1}{\sqrt{3}} \\ \Rightarrow \cos \alpha =\cos \beta=\cos \gamma=\dfrac{1}{\sqrt{3}}\end{aligned}$

So, the normal is

$ \overrightarrow{{}N}=\dfrac{1}{\sqrt{3}} \hat{i}+\dfrac{1}{\sqrt{3}} \hat{j}+\dfrac{1}{\sqrt{3}} \hat{k} $

$\therefore$ Equation of the plane is $\vec{r} \cdot \vec{N}=d$

$ \begin{aligned} & \Rightarrow \quad \vec{r} \cdot \dfrac{\vec{N}}{|\vec{N}|}=d \\ & \Rightarrow \quad \dfrac{\vec{r} \cdot(\dfrac{1}{\sqrt{3}} \hat{i}+\dfrac{1}{\sqrt{3}} \hat{j}+\dfrac{1}{\sqrt{3}} \hat{k})}{1}=3 \sqrt{3} \\ & \Rightarrow \quad \vec{r} \cdot(\dfrac{1}{\sqrt{3}} \hat{i}+\dfrac{1}{\sqrt{3}} \hat{j}+\dfrac{1}{\sqrt{3}} \hat{k})=3 \sqrt{3} \\ & \Rightarrow(x \hat{i}+y \hat{j}+z \hat{k}) \cdot \dfrac{1}{\sqrt{3}}(\hat{i}+\hat{j}+\hat{k})=3 \sqrt{3} \\ & \Rightarrow \quad x+y+z=3 \sqrt{3} \cdot \sqrt{3} \Rightarrow x+y+z=9 \end{aligned} $

Hence, the required equation of plane is $x+y+z=9$.

Solution

Direction ratios of the normal to the plane are

$(a,b,c)=(1+2,-3+1,3+3) =(3,-2,6)$

Equation of plane passing through one point $(x_1, y_1, z_1)$ is

$a(x-x_1)+b(y-y_1)+c(z-z_1) =0 $

$\Rightarrow \quad 3(x-1)-2(y+3)+6(z-3) =0 $

$\Rightarrow \quad 3 x-3-2 y-6+6 z-18 =0$

$\Rightarrow \quad 3 x-2 y+6 z-27 =0 \quad \Rightarrow 3 x-2 y+6 z=27$

Hence, the required equation is $3 x-2 y+6 z=27$.

Solution

Since, the equation of the plane passing through the points $(x_1, y_1, z_1),(x_2, y_2, z_2)$ and $(x_3, y_3, z_3)$ is

$ \begin{aligned} & \begin{vmatrix} x-x_1 & y-y_1 & z-z_1 \\ x_2-x_1 & y_2-y_1 & z_2-z_1 \\ x_3-x_1 & y_3-y_1 & z_3-z_1 \end{vmatrix} =0 \\ & \Rightarrow \begin{vmatrix} x-2 & y-1 & z-0 \\ 3-2 & -2-1 & -2-0 \\ 3-2 & 1-1 & 7-0 \end{vmatrix} =0 \Rightarrow \begin{vmatrix} x-2 & y-1 & z \\ 1 & -3 & -2 \\ 1 & 0 & 7 \end{vmatrix} =0 \\ & \Rightarrow(x-2) \begin{vmatrix} -3 & -2 \\ 0 & 7 \end{vmatrix} -(y-1) \begin{vmatrix} 1 & -2 \\ 1 & 7 \end{vmatrix} +z \begin{vmatrix} 1 & -3 \\ 1 & 0 \end{vmatrix} =0 \\ & \Rightarrow \quad(x-2)(-21)-(y-1)(7+2)+z(3)=0 \\ & \Rightarrow \quad-21(x-2)-9(y-1)+3 z=0 \\ & \Rightarrow \quad-21 x+42-9 y+9+3 z=0 \\ & \Rightarrow \quad-21 x-9 y+3 z+51=0 \Rightarrow 7 x+3 y-z-17=0 \end{aligned} $

Hence, the required equation is $7 x+3 y-z-17=0$.

Solution

Given, $\dfrac{x-3}{2} =\dfrac{y-3}{1}=\dfrac{z}{1}=\lambda$

Any point on the given line is

$x =2 \lambda+3, y=\lambda+3$ and $\quad z =\lambda$

Let P and Q be the point of intersection of two lines through the origin with the given line.

Let, coordinates of $P=(2\lambda +3, \lambda+3,\lambda)$

$\therefore$ Direction ratios of OP are $(2 \lambda+3-0),(\lambda+3-0)$ and $(\lambda-0) \Rightarrow 2 \lambda+3, \lambda+3, \lambda$

But the direction ratios of the line PQ are $2, 1,1$

$\begin{aligned}\cos \theta =\dfrac{a_1 a_2+b_1 b_2+c_1 c_2}{\sqrt{a_1^{2}+b_1^{2}+c_1^{2}} \cdot \sqrt{a_2^{2}+b_2^{2}+c_2^{2}}}\end{aligned}$

$\begin{aligned}\cos \dfrac{\pi}{3} =\dfrac{2(2 \lambda+3)+1(\lambda+3)+1 . \lambda}{\sqrt{(2)^{2}+(1)^{2}+(1)^{2}} \cdot \sqrt{(2 \lambda+3)^{2}+(\lambda+3)^{2}+\lambda^{2}}}\end{aligned} $

$\begin{aligned}\Rightarrow \quad \dfrac{1}{2} =\dfrac{4 \lambda+6+\lambda+3+\lambda}{\sqrt{6} \cdot \sqrt{4 \lambda^{2}+9+12 \lambda+\lambda^{2}+9+6 \lambda+\lambda^{2}}}\end{aligned} $

$\begin{aligned}\Rightarrow \quad \dfrac{\sqrt{6}}{2} =\dfrac{6 \lambda+9}{\sqrt{6 \lambda^{2}+18 \lambda+18}}=\dfrac{6 \lambda+9}{\sqrt{6} \sqrt{\lambda^{2}+3 \lambda+3}}\end{aligned}$

$ \begin{aligned} & \Rightarrow \quad \dfrac{6}{2}=\dfrac{3(2 \lambda+3)}{\sqrt{\lambda^{2}+3 \lambda+3}} \Rightarrow 3=\dfrac{3(2 \lambda+3)}{\sqrt{\lambda^{2}+3 \lambda+3}} \\ & \Rightarrow \quad 1=\dfrac{2 \lambda+3}{\sqrt{\lambda^{2}+3 \lambda+3}} \Rightarrow \sqrt{\lambda^{2}+3 \lambda+3}=2 \lambda+3 \\ & \Rightarrow \quad \lambda^{2}+3 \lambda+3=4 \lambda^{2}+9+12 \lambda \\ & \Rightarrow \quad 3 \lambda^{2}+9 \lambda+6=0 \quad \Rightarrow \lambda^{2}+3 \lambda+2=0 \\ & \Rightarrow \quad(\lambda+1)(\lambda+2)=0 \\ & \therefore \quad \lambda=-1, \lambda=-2 \\ & \therefore \text{ Direction ratios are }[2(-1)+3,-1+3,-1] \text{ i.e., } 1,2,-1 \text{ when } \\ & \lambda=-1 \text{ and }[2(-2)+3,-2+3,-2] \text{ i.e., }-1,1,-2 \text{ when } \lambda=-2 . \end{aligned} $

Hence, the required equations of two lines through the origin are

$ \dfrac{x}{1}=\dfrac{y}{2}=\dfrac{z}{-1} \text{ and } \dfrac{x}{-1}=\dfrac{y}{1}=\dfrac{z}{-2} . $

Solution

The given equations are

$ \begin{aligned} l+m+n & =0 \qquad…(i)\\ l^{2}+m^{2}-n^{2} & =0 \qquad…(ii) \end{aligned} $

From equation (i) $n=-(l+m)$

Putting the value of $n$ in eq. (ii) we get

$ \begin{aligned} & l^{2}+m^{2}-[-(l+m)^{2}]=0 \\ & \Rightarrow \quad l^{2}+m^{2}-l^{2}-m^{2}-2 l m=0 \\ & \Rightarrow \quad-2 lm=0 \\ & \Rightarrow \quad l m=0 \Rightarrow(-m-n) m=0 \quad [\because l=-m-n] \\ & \Rightarrow \quad(m+n) m=0 \Rightarrow m=0 \text{ or } m=-n \\ & \Rightarrow \quad l=-n \text{ or } l=0 \end{aligned} $

$\therefore$ Direction cosines of the two lines are

$0,-n, n$ and $-n, 0, n \Rightarrow 0,-1,1$ and $-1,0,1$

$\begin{aligned}\therefore \quad \cos \theta =\dfrac{(0 \hat{i}-\hat{j}+\hat{k}) \cdot(-\hat{i}+0 \hat{j}+\hat{k})}{\sqrt{(-1)^{2}+(1)^{2}} \sqrt{(-1)^{2}+(1)^{2}}}=\dfrac{1}{\sqrt{2} \cdot \sqrt{2}}=\dfrac{1}{2}\end{aligned}$

$\therefore \quad \theta =\dfrac{\pi}{3}$

Hence, the required angle is $\dfrac{\pi}{3}$.

Solution

Given that $l, m, n$ and $l+\delta l, m+\delta m, n+\delta n$, are the direction cosines of a variable line in two positions

$ \begin{aligned} \therefore \quad l^{2}+m^{2}+n^{2}=1 \qquad…(i) \end{aligned} $

$ \begin{aligned} & \text{ and }(l+\delta l)^{2}+(m+\delta m)^{2}+(n+\delta n)^{2}=1 \qquad…(ii)\\ & \Rightarrow l^{2}+\delta l^{2}+2 l . \delta l+m^{2}+\delta m^{2}+2 m . \delta m+n^{2}+\delta n^{2}+2 n . \delta n=1 \\ & \Rightarrow(l^{2}+m^{2}+n^{2})+(\delta l^{2}+\delta m^{2}+\delta n^{2})+2(l . \delta l+m . \delta m+n . \delta n)=1 \\ & \Rightarrow 1+(\delta l^{2}+\delta m^{2}+\delta n^{2})+2(l . \delta l+m . \delta m+n \cdot \delta n)=1 \\ & \Rightarrow l . \delta l+m . \delta m+n . \delta n=-\dfrac{1}{2}(\delta l^{2}+\delta m^{2}+\delta n^{2}) \end{aligned} $

Let $\vec{a}$ and $\vec{b}$ be the unit vectors along a line with direction cosines $l, m$, $n$ and $(l+\delta l),(m+\delta m),(n+\delta n)$.

$\therefore \vec{a}=l \hat{i}+m \hat{j}+n \hat{k}$ and $\vec{b}=(l+\delta l) \hat{i}+(m+\delta m) \hat{j}+(n+\delta n) \hat{k}$

$\cos \delta \theta=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}$

$\cos \delta \theta=\dfrac{(l \hat{i}+m \hat{j}+n \hat{k}) \cdot[(l+\delta l) \hat{i}+(m+\delta m) \hat{j}+(n+\delta n) \hat{k}]}{1.1}$ $\qquad [\because|\vec{a}|=|\vec{b}|=1]$

$\Rightarrow \quad \cos \delta \theta=l(l+\delta l)+m(m+\delta m)+n(n+\delta n)$

$\Rightarrow \quad \cos \delta \theta=l^{2}+l . \delta l+m^{2}+m . \delta m+n^{2}+n . \delta n$

$\Rightarrow \quad \cos \delta \theta=(l^{2}+m^{2}+n^{2})+(l . \delta l+m . \delta m+n . \delta n)$

$\Rightarrow \quad \cos \delta \theta=1-\dfrac{1}{2}(\delta l^{2}+\delta m^{2}+\delta n^{2})$

$\Rightarrow 1-\cos \delta \theta=\dfrac{1}{2}(\delta l^{2}+\delta m^{2}+\delta n^{2})$

$\Rightarrow 2 \sin ^{2} \dfrac{\delta \theta}{2}=\dfrac{1}{2}(\delta l^{2}+\delta m^{2}+\delta n^{2})$

$\Rightarrow 4 \sin ^{2} \dfrac{\delta \theta}{2}=\delta l^{2}+\delta m^{2}+\delta n^{2}$

$ \Rightarrow 4(\dfrac{\delta \theta}{2})^{2}=\delta l^{2}+\delta m^{2}+\delta n^{2}\qquad \begin{bmatrix} \because \quad \dfrac{\delta \theta}{2} \text{ is very small so, } \sin \dfrac{\delta \theta}{2}=\dfrac{\delta \theta}{2} \end{bmatrix} $

$\Rightarrow \quad(\delta \theta)^{2}=\delta l^{2}+\delta m^{2}+\delta n^{2}$

Hence proved

Solution

We have $A(a, b, c)$ and $O(0,0,0)$

$\therefore$ Direction ratios of $OA=a-0, b-0, c-0 =a, b, c$

$\therefore$ Direction cosines of line $OA =\dfrac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}, \dfrac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}, \dfrac{c}{\sqrt{a^{2}+b^{2}+c^{2}}} $

Now direction ratios of the normal to the plane are $(a, b, c)$.

$\therefore$ Equation of the plane passing through the point $A(a, b, c)$ is

$ a(x-a)+b(y-b)+c(z-c)=0 $

$ \begin{aligned} \Rightarrow a x-a^{2}+b y-b^{2}+c z-c^{2} =0 \\ \Rightarrow a x+b y+c z =a^{2}+b^{2}+c^{2} \end{aligned} $

Hence, the required equation is $a x+b y+c z=a^{2}+b^{2}+c^{2}$.

Solution

Let OX, OY, OZ and OX’, OY’, OZ’ be two rectangular systems

Given the plane cuts rectengular axis at distances $a, b, c$ and $a^{\prime}, b^{\prime}, c^{\prime}$ respectively from the origin.

$\therefore$ Equations of two planes are

$$ \begin{equation*} \dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1 \ldots(i) \quad \text{ and } \quad \dfrac{x}{a^{\prime}}+\dfrac{y}{b^{\prime}}+\dfrac{z}{c^{\prime}}=1 \ldots(ii) \end{equation*} $$

Length of perpendicular from origin to plane $(i)$ is

$ =\Bigg|\dfrac{\dfrac{0}{a}+\dfrac{0}{b}+\dfrac{0}{c}-1}{\sqrt{\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}+\dfrac{1}{c^{2}}}}\Bigg|=\dfrac{1}{\sqrt{\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}+\dfrac{1}{c^{2}}}} $

Length of perpendicular from origin to plane (ii)

$ =\Bigg|\dfrac{\dfrac{0}{a^{\prime}}+\dfrac{0}{b^{\prime}}+\dfrac{0}{c^{\prime}}-1}{\sqrt{\dfrac{1}{a^{\prime 2}}+\dfrac{1}{b^{\prime 2}}+\dfrac{1}{c^{\prime 2}}}}\Bigg|=\dfrac{1}{\sqrt{\dfrac{1}{a^{\prime 2}}+\dfrac{1}{b^{\prime 2}}+\dfrac{1}{c^{\prime 2}}}} $

As per the condition of the question

$ \dfrac{1}{\sqrt{\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}+\dfrac{1}{c^{2}}}}=\dfrac{1}{\sqrt{\dfrac{1}{a^{\prime 2}}+\dfrac{1}{b^{\prime 2}}+\dfrac{1}{c^{\prime 2}}}} $

Hence, $\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}+\dfrac{1}{c^{2}}=\dfrac{1}{a^{\prime 2}}+\dfrac{1}{b^{\prime 2}}+\dfrac{1}{c^{\prime 2}}$

Solution

Given that: $\quad \dfrac{4-x}{2}=\dfrac{y}{6}=\dfrac{1-z}{3}$ is the equation of line

$ \Rightarrow \quad \dfrac{x-4}{-2}=\dfrac{y}{6}=\dfrac{z-1}{-3}=\lambda $

$\therefore$ Coordinates of any point $Q$ on the line are $x=-2 \lambda+4, y=6 \lambda$ and $z=-3 \lambda+1$ and the given point is $P(2,3,-8)$

Direction ratios of PQ are $-2 \lambda+4-2,6 \lambda-3,-3 \lambda+1+8$

i.e., $-2 \lambda+2,6 \lambda-3,-3 \lambda+9$

and the direction ratios of the given line are $-2,6,-3$.

If PQ is perpendicular to the given line then,

$-2(-2 \lambda+2)+6(6 \lambda-3)-3(-3 \lambda+9)=0$

$\Rightarrow \quad 4 \lambda-4+36 \lambda-18+9 \lambda-27=0$

$\Rightarrow \quad 49 \lambda-49=0 \Rightarrow \lambda=1$

$\therefore$ The foot of the perpendicular is $-2(1)+4,6(1),-3(1)+1$

i.e., $2,\ 6,\ -2$

$ \begin{aligned} \text{ Now, distance P Q } & =\sqrt{(2-2)^{2}+(3-6)^{2}+(-8+2)^{2}} \\ & =\sqrt{9+36}=\sqrt{45}=3 \sqrt{5} \end{aligned} $

Hence, the required coordinates of the foot of perpendicular are $2,6,-2$ and the required distance is $3 \sqrt{5}$ units.

Solution

The given equation of line is

$ \dfrac{x+5}{1}=\dfrac{y+3}{4}=\dfrac{z-6}{-9}=\lambda$ and given point is $P(2,4,-1)$

Let $Q$ be any point on the given line

$\therefore$ Coordinates of $Q$ are $x=\lambda-5, y=4 \lambda-3, z=-9 \lambda+6$

Direction ratios of PQ are $\lambda-5-2,4 \lambda-3-4,-9 \lambda+6+1$ i.e., $\lambda-7,4 \lambda-7,-9 \lambda+7$

Direction ratios of the line are $1,4,-9$

If PQ is perpendicular to the given line then

$ \begin{aligned} & 1(\lambda-7)+4(4 \lambda-7)-9(-9 \lambda+7) =0 \\ & \lambda-7+16 \lambda-28+81 \lambda-63 =0 \\ & \Rightarrow \quad 98 \lambda-98 =0 \\ & \therefore \quad \lambda = 1 \end{aligned} $

So, the coordinates of $Q$ are $1-5,4 \times 1-3,-9 \times 1+6$ i.e., $-4,1,-3$

$ \begin{aligned} \therefore \quad PQ & =\sqrt{(-4-2)^{2}+(1-4)^{2}+(-3+1)^{2}} \\ & =\sqrt{(-6)^{2}+(-3)^{2}+(-2)^{2}}=\sqrt{36+9+4}=\sqrt{49}=7 \end{aligned} $

Hence, the required distance is 7 units.

Solution

Given plane is $2 x-2 y+4 z+5=0$ and given point is $(1, \dfrac{3}{2}, 2)$

Direction ratios of the normal to the plane are 2, - 2, 4

So, the equation of the line passing through $(1, \dfrac{3}{2}, 2)$ and whose direction ratios are equal to the direction ratios of the normal to the plane i.e., $2,-2,4$ is $\dfrac{x-1}{2}=\dfrac{y-\dfrac{3}{2}}{-2}=\dfrac{z-2}{4}=\lambda$

$\therefore$ Coordinates of any point in the plane is $\left(2 \lambda+1,-2 \lambda+\dfrac{3}{2}, 4 \lambda+2\right)$

To find the foot of perpendicular, let the point $\left(2 \lambda+1,-2 \lambda+\dfrac{3}{2}, 4 \lambda+2\right)$ lies on the plane

Since, the point lies in the plane, then

$2(2 \lambda+1)-2(-2 \lambda+\dfrac{3}{2})+4(4 \lambda+2)+5=0$

$\Rightarrow 4 \lambda+2+4 \lambda-3+16 \lambda+8+5=0$

$\Rightarrow 24 \lambda+12=0 \quad \therefore \lambda=-\dfrac{1}{2}$

So, the coordinates of the point in the plane are

$ 2(-\dfrac{1}{2})+1,-2(-\dfrac{1}{2})+\dfrac{3}{2}, 4(-\dfrac{1}{2})+2 \text{ i.e., } 0, \dfrac{5}{2}, 0 $

Hence, the foot of the perpendicular is $(0, \dfrac{5}{2}, 0)$ and the

$ \begin{aligned} \therefore \text{Required length} \quad & =\sqrt{(1-0)^{2}+(\dfrac{3}{2}-\dfrac{5}{2})^{2}+(2-0)^{2}} \\ & =\sqrt{1+1+4}=\sqrt{6} \text{ units } \end{aligned} $

Solution

Given point is $(3,0,1)$ and the given equation of planes are

$$ \quad \begin{aligned} x+2 y & =0 \ldots(i) \\ 3 y-z & =0 \ldots(i) \end{aligned}$$

Equation of any line $l$ passing through $(3,0,1)$ is

$l: \dfrac{x-3}{a}=\dfrac{y-0}{b}=\dfrac{z-1}{c}$

Direction ratios of the normal to plane (i) and plane (ii) are

$(1,2,0)$ and $(0,3,-1)$

Since the line is parallel to both the planes.

$ \begin{matrix} \therefore & 1 \cdot a+2 \cdot b+0 . c=0 \Rightarrow a+2 b+0 c=0 \\ \text{ and } & 0 \cdot a+3 \cdot b-1 . c=0 \Rightarrow 0 \cdot a+3 b-c=0 \end{matrix} $

So

$ \dfrac{a}{-2-0}=\dfrac{-b}{-1-0}=\dfrac{c}{3-0}=\lambda $

$\therefore a=-2 \lambda, b=\lambda, c=3 \lambda$

So, the equation of line is

$ \dfrac{x-3}{-2 \lambda}=\dfrac{y}{\lambda}=\dfrac{z-1}{3 \lambda} $

Hence, the required equation is $\dfrac{x-3}{-2}=\dfrac{y}{1}=\dfrac{z-1}{3}$

or in vector form is

$ (x-3) \hat{i}+y \hat{j}+(z-1) \hat{k}=\lambda(-2 \hat{i}+\hat{j}+3 \hat{k}) $

Solution

Equation of the plane passing through two points $(x_1, y_1, z_1)$ and $(x_2, y_2, z_2)$ with its normal’s direction ratios $(a, b, c)$ is

$$ \begin{equation*} a(x-x_1)+b(y-y_1)+c(z-z_1)=0 \ldots(i) \end{equation*} $$

If the plane is passing through $(x_2, y_2, z_2)$ then

$$a(x_2-x_1)+b(y_2-y_1)+c(z_2-z_1) =0$$

Since, plane is passing through (2,1,-1) and (-1,3,4) then

$$ \begin{align*} & & a(-1-2)+b(3-1)+c(4+1) & =0 \\ \Rightarrow & & -3 a+2 b+5 c & =0 \ldots(ii) \end{align*} $$

Since the required plane is perpendicular to the given plane $x-2 y+4 z=10$, then

$$ \begin{equation*} 1 . a-2 . b+4 . c=10 \ldots(iii) \end{equation*} $$

Solving (ii) and (iii) we get,

$ \dfrac{a}{8+10}=\dfrac{-b}{-12-5}=\dfrac{c}{6-2}=\lambda $

$a=18 \lambda, b=17 \lambda, c=4 \lambda$

Hence, the required plane is

$ \begin{matrix} 18 \lambda(x-2)+17 \lambda(y-1)+4 \lambda(z+1) =0 \\ \Rightarrow 18 x-36+17 y-17+4 z+4 =0 \\ \Rightarrow 18 x+17 y+4 z-49 =0 \end{matrix} $

Solution

Given equations of lines are

$$ \begin{align*} \vec{r} & =(8+3 \lambda) \hat{i}-(9+16 \lambda) \hat{j}+(10+7 \lambda) \hat{k} \ldots(i)\\ \text{ and } \quad \vec{r} & =15 \hat{i}+29 \hat{j}+5 \hat{k}+\mu(3 \hat{i}+8 \hat{j}-5 \hat{k}) \ldots(ii) \end{align*} $$

Equation (i) can be re-written as

$$ \begin{equation*} \vec{r}=8 \hat{i}-9 \hat{j}+10 \hat{k}+\lambda(3 \hat{i}-16 \hat{j}+7 \hat{k}) \ldots(iii) \end{equation*} $$

Here, $\quad \vec{a} _1=8 \hat{i}-9 \hat{j}+10 \hat{k}$ and $ \vec{a} _2=15 \hat{i}+29 \hat{j}+5 \hat{k}$

$ \begin{aligned} \vec{b} _1 & =3 \hat{i}-16 \hat{j}+7 \hat{k} \text{ and } \vec{b} _2=3 \hat{i}+8 \hat{j}-5 \hat{k} \\ \vec{a} _2- \vec{a} _1 & =7 \hat{i}+38 \hat{j}-5 \hat{k} \\ \vec{b} _1 \times \vec{b} _2 & = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & -16 & 7 \\ 3 & 8 & -5 \end{vmatrix} \end{aligned} $

$ \begin{aligned} & =\hat{i}(80-56)-\hat{j}(-15-21)+\hat{k}(24+48) \\ & =24 \hat{i}+36 \hat{j}+72 \hat{k} \end{aligned} $

$\therefore$ Shortest distance, SD $\begin{aligned}=|\dfrac{( \vec{a} _2- \vec{a} _1) \cdot( \vec{b} _1 \times \vec{b} _2)}{| \vec{b} _1 \times \vec{b} _2|}|\end{aligned}$

$ \begin{aligned} & =|\dfrac{(7 \hat{i}+38 \hat{j}-5 \hat{k}) \cdot(24 \hat{i}+36 \hat{j}+72 \hat{k})}{\sqrt{(24)^{2}+(36)^{2}+(72)^{2}}}| \\ & =|\dfrac{168+1368-360}{\sqrt{576+1296+5184}}|=|\dfrac{168+1008}{\sqrt{7056}}|=\dfrac{1176}{84}=14 \text{ units } \end{aligned} $

Hence, the required distance is 14 units.

Solution

The given planes are

$P_1: \quad 5 x+3 y+6 z+8=0$

$P_2: \quad x+2 y+3 z-4=0$

$P_3: \quad 2 x+y-z+5=0$

Equation of the plane passing through the line of intersection of $P_2$ and $P_3$ is

$ (x+2 y+3 z-4)+\lambda(2 x+y-z+5)=0 $

$ \begin{aligned} \Rightarrow \quad(1+2 \lambda) x+(2+\lambda) y+(3-\lambda) z-4+5 \lambda=0 \ldots(i) \end{aligned} $

Plane (i) is perpendicular to $P_1$, then

$5(1+2 \lambda)+3(2+\lambda)+6(3-\lambda) =0 $

$\Rightarrow \quad 5 5+10 \lambda+6+3 \lambda+18-6 \lambda =0$

$\Rightarrow \quad 7 \lambda+29 =0 $

$\therefore \quad \lambda =\dfrac{-29}{7}$

Putting the value of $\lambda$ in eq. (i), we get

$ \begin{aligned} & {\left[1+2\left(\dfrac{-29}{7}\right)\right] x+\bigg[2-\dfrac{29}{7}\bigg] y+\bigg[3+\dfrac{29}{7}\bigg] z-4+5\bigg(\dfrac{-29}{7}\bigg)=0} \\ & \Rightarrow \dfrac{-51}{7} x-\dfrac{15}{7} y+\dfrac{50}{7} z-4-\dfrac{145}{7}=0 \\ & \Rightarrow-51 x-15 y+50 z-28-145=0 \\ & \Rightarrow-51 x-15 y+50 z-173=0 \\ &\Rightarrow 51 x+15 y-50 z+173=0 \end{aligned} $

Solution

Given planes are:

$ \begin{aligned} a x+b y & =0 \ldots(i)\\ z & =0 \ldots(ii) \end{aligned} $

Equation of any plane passing through the line of intersection of plane (i) and (ii) is

$ \begin{aligned} (a x+b y)+k z=0 \Rightarrow a x+b y+k z=0 \ldots(iii) \end{aligned} $

Dividing both sides by $\sqrt{a^{2}+b^{2}+k^{2}}$, we get

$\begin{aligned}\dfrac{a}{\sqrt{a^{2}+b^{2}+k^{2}}} x+\dfrac{b}{\sqrt{a^{2}+b^{2}+k^{2}}} y+\dfrac{k}{\sqrt{a^{2}+b^{2}+k^{2}}} z=0\end{aligned}$

$\therefore$ Direction cosines of the normal to the plane are

$\begin{aligned}\dfrac{a}{\sqrt{a^{2}+b^{2}+k^{2}}}, \dfrac{b}{\sqrt{a^{2}+b^{2}+k^{2}}}, \dfrac{k}{\sqrt{a^{2}+b^{2}+k^{2}}}\end{aligned}$

and the direction cosines of the plane ( $i$ ) are

$\begin{aligned}\dfrac{a}{\sqrt{a^{2}+b^{2}}}, \dfrac{b}{\sqrt{a^{2}+b^{2}}}, 0\end{aligned}$

Since, $\alpha$ is the angle between the planes (i) and (iii), we get

$ \begin{aligned} & \cos \alpha=\dfrac{a \cdot a+b \cdot b+k \cdot 0}{\sqrt{a^{2}+b^{2}+k^{2}} \cdot \sqrt{a^{2}+b^{2}}} \\ & \Rightarrow \quad \cos \alpha=\dfrac{a^{2}+b^{2}}{\sqrt{a^{2}+b^{2}+k^{2}} \cdot \sqrt{a^{2}+b^{2}}} \\ & \Rightarrow \quad \cos \alpha=\dfrac{\sqrt{a^{2}+b^{2}}}{\sqrt{a^{2}+b^{2}+k^{2}}} \Rightarrow \cos ^{2} \alpha=\dfrac{a^{2}+b^{2}}{a^{2}+b^{2}+k^{2}} \\ & \Rightarrow(a^{2}+b^{2}+k^{2}) \cos ^{2} \alpha=a^{2}+b^{2} \\ & \Rightarrow a^{2} \cos ^{2} \alpha+b^{2} \cos ^{2} \alpha+k^{2} \cos ^{2} \alpha=a^{2}+b^{2} \\ & \Rightarrow \quad k^{2} \cos ^{2} \alpha=a^{2}-a^{2} \cos ^{2} \alpha+b^{2}-b^{2} \cos ^{2} \alpha \\ & \Rightarrow \quad k^{2} \cos ^{2} \alpha=a^{2}(1-\cos ^{2} \alpha)+b^{2}(1-\cos ^{2} \alpha) \\ & \Rightarrow \quad k^{2} \cos ^{2} \alpha=a^{2} \sin ^{2} \alpha+b^{2} \sin ^{2} \alpha \\ & \Rightarrow \quad k^{2} \cos ^{2} \alpha=(a^{2}+b^{2}) \sin ^{2} \alpha \\ & \Rightarrow \quad k^{2}=(a^{2}+b^{2}) \dfrac{\sin ^{2} \alpha}{\cos ^{2} \alpha} \Rightarrow k= \pm \sqrt{a^{2}+b^{2}} \cdot \tan \alpha \end{aligned} $

Putting the value of $k$ in eq. (iii) we get

$a x+b y \pm(\sqrt{a^{2}+b^{2}} \cdot \tan \alpha) z=0$ which is the required equation of plane.

Hence proved.

Solution

Given planes are;

and $\begin{aligned} \quad \vec{r} \cdot(\hat{i}+3 \hat{j})-6=0 \quad & \Rightarrow \quad x+3 y-6=0 \qquad…(i) \\ \quad \vec{r} \cdot(3 \hat{i}-\hat{j}-4 \hat{k})=0 & \Rightarrow \quad 3 x-y-4 z=0 \qquad…(ii) \end{aligned}$

Equation of the plane passing through the line of intersection of plane (i) and (ii) is

$$ \begin{matrix} (x+3 y-6)+k(3 x-y-4 z)=0 \qquad…(iii)\\ (1+3 k) x+(3-k) y-4 k z-6=0 \end{matrix} $$

Perpendicular distance from origin

$\begin{aligned}=\bigg|\dfrac{-6}{\sqrt{(1+3 k)^{2}+(3-k)^{2}+(-4 k)^{2}}}\bigg|=1\end{aligned}$

$\begin{aligned}\Rightarrow \dfrac{36}{1+9 k^{2}+6 k+9+k^{2}-6 k+16 k^{2}}=1\end{aligned} \qquad$ [Squaring both sides]

$\begin{aligned}\Rightarrow \quad \dfrac{36}{26 k^{2}+10}=1 \Rightarrow 26 k^{2}+10=36\end{aligned}$

$\Rightarrow \quad 26 k^{2}=26 \quad \Rightarrow \quad k^{2}=1 \quad \therefore k= \pm 1$

Putting the value of $k$ in eq. (iii) we get,

$ (x+3 y-6) \pm(3 x-y-4 z)=0 $

$\Rightarrow x+3 y-6+3 x-y-4 z=0$ and $x+3 y-6-3 x+y+4 z=0$

$\Rightarrow 4 x+2 y-4 z-6=0$ and $-2 x+4 y+4 z-6=0$

Hence, the required equations are:

$4 x+2 y-4 z-6=0$ and $-2 x+4 y+4 z-6=0$.

Solution

Given points are $P(\hat{i}-\hat{j}+3 \hat{k})$ and $Q(3 \hat{i}+3 \hat{j}+3 \hat{k})$ and the plane $\vec{r} .(5 \hat{i}+2 \hat{j}-7 \hat{k})+9=0$

Perpendicular distance of $P(\hat{i}-\hat{j}+3 \hat{k})$ from the plane $\vec{r} .(5 \hat{i}+2 \hat{j}-7 \hat{k})+9=0$

$ \begin{aligned} & =\bigg|\dfrac{(\hat{i}-\hat{j}+3 \hat{k}) \cdot(5 \hat{i}+2 \hat{j}-7 \hat{k})+9}{\sqrt{(5)^{2}+(2)^{2}+(-7)^{2}}}\bigg| \\ & =\bigg|\dfrac{5-2-21+9}{\sqrt{25+4+49}}\bigg|=\bigg|\dfrac{-9}{\sqrt{78}}\bigg| \end{aligned} $

Perpendicular distance of $Q(3 \hat{i}+3 \hat{j}+3 \hat{k})$ from the plane $\vec{r} .(5 \hat{i}+2 \hat{j}-7 \hat{k})+9=0$

$ \begin{aligned} & =\bigg|\dfrac{(3 \hat{i}+3 \hat{j}+3 \hat{k}) \cdot(5 \hat{i}+2 \hat{j}-7 \hat{k})+9}{\sqrt{25+4+49}}\bigg| \\ & =\bigg|\dfrac{15+6-21+9}{\sqrt{78}}|=|\dfrac{9}{\sqrt{78}}\bigg| \end{aligned} $

Hence, the two points are equidistant from the given plane. Opposite sign shows that they lie on either side of the plane.

Solution

Position vector of $A$ is $6 \hat{i}+7 \hat{j}+4 \hat{k}$ and $\overrightarrow{{}AB}=3 \hat{i}-\hat{j}+\hat{k}$

So, equation of any line passing through $A$ and parallel to $\overrightarrow{{}AB}$

$$ \begin{equation*} \vec{r}=(6 \hat{i}+7 \hat{j}+4 \hat{k})+\lambda(3 \hat{i}-\hat{j}+\hat{k}) \qquad…(i) \end{equation*} $$

Now any point $P$ on $\overrightarrow{{}AB}=(6+3 \lambda, 7-\lambda, 4+\lambda)$

Similarly, position vector of $C$ is $-9 \hat{j}+2 \hat{k}$

and $\overrightarrow{{}CD}=-3 \hat{i}+2 \hat{j}+4 \hat{k}$

So, equation of any line passing through $C$ and parallel to $\overrightarrow{{}CD}$ is

$$ \begin{equation*} \vec{r}=(-9 j+2 \hat{k})+\mu(-3 \hat{i}+2 \hat{j}+4 \hat{k}) \qquad…(ii) \end{equation*} $$

Any point $Q$ on $\overrightarrow{{}CD}=(-3 \mu,-9+2 \mu, 2+4 \mu)$

Direction ratios of $\overrightarrow{{}PQ}$ are

$ (6+3 \lambda+3 \mu, 7-\lambda+9-2 \mu, 4+\lambda-2-4 \mu) $

$\Rightarrow(6+3 \lambda+3 \mu),(16-\lambda-2 \mu),(2+\lambda-4 \mu)$

Now $\overrightarrow{{}PQ}$ is $\perp$ to eq. (i), then

$3(6+3 \lambda+3 \mu)-1(16-\lambda-2 \mu)+1(2+\lambda-4 \mu)=0$

$\Rightarrow 18+9 \lambda+9 \mu-16+\lambda+2 \mu+2+\lambda-4 \mu=0 $

$\Rightarrow 11 \lambda+7 \mu+4=0\qquad $…(iii)

$\overrightarrow{{}PQ} \text{ is also } \perp \text{ to eq. }(\text{ ii }) \text{, then }$

$-3(6+3 \lambda+3 \mu)+2(16-\lambda-2 \mu)+4(2+\lambda-4 \mu)=0 $

$\Rightarrow -18-9 \lambda-9 \mu+32-2 \lambda-4 \mu+8+4 \lambda-16 \mu=0 $

$\Rightarrow -7 \lambda-29 \mu+22=0 $

$\Rightarrow 7 \lambda+29 \mu-22=0 \qquad $…(iv)

Solving eq. (iii) and (iv) we get

$ \begin{aligned} 77 \lambda+49 \mu+28=0 \\ 77 \lambda+319 \mu-242=0 \\ (-)\quad(-) \quad (+) \quad (-) \\ \hline -270\mu+270=0 \end{aligned} $

$\therefore \mu=1$

Now using $\mu=1$ in eq. (iv) we get

$ 7 \lambda+29-22=0 \Rightarrow \lambda=-1 $

$\therefore$ Position vector of $P=[6+3(-1), 7+1,4-1]=(3,8,3)$

and position vector of $Q=[-3(1),-9+2(1), 2+4(1)]=(-3,-7,6)$

Hence, the position vectors of

$ P=3 \hat{i}+8 \hat{j}+3 \hat{k} \text{ and } Q=-3 \hat{i}-7 \hat{j}+6 \hat{k} $

Solution

Given, $2 l+2 m-n=0\quad \ldots (i)$ and

$\quad m n+n l+l m=0 \quad \ldots (ii)$

From equation (i), $m=\dfrac{n-2 l}{2}$

Substituting the value of $m$ in equation (ii), we get

$ \begin{aligned} & (\dfrac{n-2 l}{2}) n+n l+l(\dfrac{n-2 l}{2})=0 \\ \Rightarrow & \dfrac{n^{2}-2 n l+2 n l+n l-2 l^{2}}{2}=0 \\ \Rightarrow & n^{2}+n l-2 l^{2}=0 \\ \Rightarrow & n^{2}+2 n l-n l-2 l^{2}=0 \\ \Rightarrow & n(n+2 l)-l(n+2 l)=0 \\ \Rightarrow & (n-l)(n+2 l)=0 \\ \Rightarrow & n=-2 l \quad \text{ and } \quad n=l \\ \therefore \quad & m=\dfrac{-2 l-2 l}{2}, \quad m=\dfrac{l-2 l}{2} \\ \Rightarrow & m=-2 l, \quad m=\dfrac{-l}{2} \end{aligned} $

Therefore, the direction ratios are proportional to $l,-2 l,-2 l$ and $l, \dfrac{-l}{2}, l$.

$\Rightarrow 1,-2,-2$ and $2,-1,2$

If the two lines are perpendicular to each other then

$ \begin{aligned} 1(2)-2(-1)-2 \times 2 & =0 \\ 2+2-4 & =0 \\ 0 & =0 \end{aligned} $

Hence, the two lines are perpendicular.

Solution

Let $\vec{a}, \vec{b}, \vec{c}$ and $\vec{d}$ are such that

$ \vec{a}=l_1 \hat{i}+m_1 \hat{j}+n_1 \hat{k} $

$ \begin{aligned} \vec{b} & =l_2 \hat{i}+m_2 \hat{j}+n_2 \hat{k} \\ \vec{c} & =l_3 \hat{i}+m_3 \hat{j}+n_3 \hat{k} \end{aligned} $

and $\vec{d}=(l_1+l_2+l_3) \hat{i}+(m_1+m_2+m_3) \hat{j}+(n_1+n_2+n_3) \hat{k}$

Since the given direction cosines are mutually perpendicular then

$ \begin{aligned} & l_1 l_2+m_1 m_2+n_1 n_2=0 \\ & l_2 l_3+m_2 m_3+n_2 n_3=0 \\ & l_1 l_3+m_1 m_3+n_1 n_3=0 \\ & l_1^2+m_1^2+n_1=1 \\ & l_2^2+m_2^2+n_2^2=1 \\ & l_3^2+m_3^2+n_3^2=1 \end{aligned} $

$ \begin{array}{l} \therefore\left(l_1+l_2+l_3\right)^2+\left(m_1+m_2+m_3\right)^2+\left(n_1+n_2n_3\right)^2 \ =\left(l_{1}^{2}+m_{1}^{2}+n_{1}^{2}\right)+\left(l_{2}^{2}+m_{2}^{2}+n_{2}^{2}\right)+\left(l_{3}^{2}+m_{3}^{2}+n_{3}^{2}\right)+2\left(l_{1} l_{2}+m_{1} m_{2}\right. \left.+n_{1} n_{2}\right) \+2\left(l_{1} l_{2}+m_{1} m_{3}+n_{1} n_{3}\right)+2\left(l_{2} l_{3}+m_{2} m_{3}+n_{2} n_{3}\right)\ = 1 + 1 + 1 + 2 \times 0+2 \times 0+2 \times 0\ =3 \end{array} $

$$ \Rightarrow \sqrt{\left(l_{1}+l_{2}+l_{3}\right)^{2}+\left(m_{1}+m_{2}+m_{3}\right)^{2}+\left(n_{1}+n_{2}+n_{3}\right)^{2}}=\sqrt{3} $$

Let $\alpha, \beta$ and $\gamma$ be the angles between $\vec{a}$ and $\vec{d}, \vec{b}$ and $\vec{d}, \vec{c}$ and $\vec{d}$ respectively.

$$ \cos\alpha=\dfrac{\left\lbrack\left.l_1(l_1+l_2+l_3\right)+m_1(m_1+m_2+m_3)+n_1\left(n_1+n_2+n_3)\right\rbrack\right.}{\sqrt{l_1^2+m_1^2+n_1^2}\sqrt{\left.(l_1+l_2+l_3\right)^2+\left(m_1+m_2+m_3\right)^2+\left(n_1+n_2+n_3\right)^2}^{}} $$

$ \begin{aligned} \therefore \cos \alpha & =\dfrac{\left\lbrack\left.l_1(l_1+l_2+l_3\right)+m_1(m_1+m_2+m_3)+n_1\left(n_1+n_2+n_3)\right\rbrack\right.}{\sqrt{3}\ } \\ & =\dfrac{l_1^{2}+l_1 l_2+l_1 l_3+m_1^{2}+m_1 m_2+m_1 m_3+n_1^{2}+n_1 n_2+n_1 n_3}{\sqrt{3}} \\ & =\dfrac{(l_1^{2}+m_1^{2}+n_1^{2})+(l_1 l_2+m_1 m_2+n_1 n_2)+(l_1 l_3+m_1 m_3+n_1 n_3)}{\sqrt{3}} \\ & =\dfrac{1+0+0}{\sqrt{3}} \\ & = \dfrac{1}{\sqrt{3}} \ \therefore \cos \beta & =\dfrac{l_2(l_1+l_2+l_3)+m_2(m_1+m_2+m_3)+n_2(n_1+n_2+n_3)}{\sqrt{l_2^2+m_2^2+n_2^2}\sqrt{\left.(l_1+l_2+l_3\right)^2+\left(m_1+m_2+m_3\right)^2+\left(n_1+n_2+n_3\right)^2}^{}} \\ & =\dfrac{l_1 l_2+l_2^{2}+l_2 l_3+m_1 m_2+m_2^{2}+m_2 m_3+n_1 n_2+n_2^{2}+n_2 n_3}{\sqrt{3}} \\ & =\dfrac{(l_2^{2}+m_2^{2}+n_2^{2})+(l_1 l_2+m_1 m_2+n_1 n_2)+(l_2 l_3+m_2 m_3+n_2 n_3)}{\sqrt{3}} \\ & = \dfrac{1+0+0}{\sqrt{3}} \ & = \dfrac{1}{\sqrt{3}} \end{aligned} $

Similarly,

$ \begin{aligned} \therefore \cos \gamma & =\dfrac{l_3(l_1+l_2+l_3)+m_3(m_1+m_2+m_3)+n_3(n_1+n_2+n_3)}{\sqrt{l_3^2+m_3^2+n_3^2}\sqrt{\left.(l_1+l_2+l_3\right)^2+\left(m_1+m_2+m_3\right)^2+\left(n_1+n_2+n_3\right)^2}^{}} \\ & =\dfrac{l_1 l_3+l_2 l_3+l_3^{2}+m_1 m_3+m_2 m_3+m_3^{2}+n_1 n_3+n_2 n_3+n_3^{2}}{\sqrt{3}} \\ & = \dfrac{(l_3^{2}+m_3^{2}+n_3^{2})+(l_1 l_3+m_1 m_3+n_1 n_3)+(l_2 l_3+m_2 m_3+n_2 n_3)}{\sqrt{3}} \\ & =\dfrac{1+0+0}{\sqrt{3}}\ & = \dfrac{1}{\sqrt{3}} \end{aligned} $

$\therefore \cos \alpha=\cos \beta=\cos \gamma=\dfrac{1}{\sqrt{3}} \Rightarrow \alpha=\beta=\gamma$ which is the required result.

Solution

The given point is $(\alpha, \beta, \gamma)$

Any point on $y$-axis $=(0, \beta, 0)$

$\therefore$ Required distance $=\sqrt{(\alpha-0)^{2}+(\beta-\beta)^{2}+(\gamma-0)^{2}}$

$ =\sqrt{\alpha^{2}+\gamma^{2}} $

Hence, the correct option is (d).

Solution

If $l, m, n$ are the direction cosines of a line, then

$l^{2}+m^{2}+n^{2} =1 $

$\text{ So, } \quad k^{2}+k^{2}+k^{2} =1 $

$ \quad \Rightarrow 3 k^{2} =1 \Rightarrow k= \pm \dfrac{1}{\sqrt{3}}$

Hence, the correct option is (d).

Solution

Given that: $\vec{r} \cdot(\dfrac{2}{7} \hat{i}+\dfrac{3}{7} \hat{j}-\dfrac{6}{7} \hat{k})=1$

The distance d of a plane from the origin given in the form $\vec{r}.\vec{n}=d_0$ is calculated as:

$$d=\left|\dfrac{d_0}{|\vec{n}|}\right|$$

So, the distance of the given plane from the origin is

$\begin{aligned}=\bigg|\dfrac{1}{\sqrt{(\dfrac{2}{7})^{2}+(\dfrac{3}{7})^{2}+(\dfrac{-6}{7})^{2}}}\bigg|=\bigg|\dfrac{1}{\sqrt{\dfrac{4}{49}+\dfrac{9}{49}+\dfrac{36}{49}}}\bigg|=\dfrac{1}{1}=1\end{aligned}$

Hence, the correct option is $(a)$.

Solution

Given line $\quad l: \dfrac{x-2}{3}=\dfrac{y-3}{4}=\dfrac{z-4}{5}$

and plane $\quad P: 2 x-2 y+z=5$

Direction ratios of the line are $3,4,5$

Direction ratios of the normal to the plane are $2,-2,1$

Let, $ \theta $ is the angle between the line $ l $ and the plane $ P $. Therefore, the angle between the normal to the plane and the line is $ 90^\circ - \theta $.

Now, $\cos (90^{\circ}-\theta)=\sin \theta = \dfrac{\left| a_1 b_1 + a_2 b_2 + a_3 b_3 \right|}{\sqrt{a_1^2 + a_2^2 + a_3^2} \cdot \sqrt{b_1^2 + b_2^2 + b_3^2}}$

Here : $\quad$ $a_1​,a_2​,a_3​$ are the direction ratios of the line.

$b_1​,b_2​,b_3$​ are the direction ratios of the normal to the plane.

$ \begin{matrix} \therefore & \sin \theta=\dfrac{3(2)+4(-2)+5(1)}{\sqrt{9+16+25} \cdot \sqrt{4+4+1}} \\ \Rightarrow & \sin \theta=\dfrac{6-8+5}{\sqrt{50} \cdot 3} \Rightarrow \dfrac{3}{5 \sqrt{2} \cdot 3}=\dfrac{1}{5 \sqrt{2}}=\dfrac{\sqrt{2}}{10} \end{matrix} $

Hence, the correct option is $(d)$.

Solution

To find the reflection of a point $(\alpha,\beta,\gamma)$ in the $ x y $-plane, you need to consider how the $ x y $ -plane affects the coordinates of the point.

The $ x y $-plane is defined by $ z=0 $. To reflect a point across this plane, you keep the $ x $ and $ y $ coordinates the same and negate the $ z $ coordinate.

Thus, the reflection of the point $(\alpha,\beta,\gamma)$ in the $ x y $-plane is $(\alpha,\beta,-\gamma)$.

Hence, the correct option is $(d)$.

Solution

Given points are $A(0,4,1), B(2,3,-1), C(4,5,0)$ and $D(2,6,2)$

Direction ratios of $AB=2,-1-2$

Direction ratios of $D C=2,-1,-2$

$\therefore AB || DC$

Similarly, direction ratios of $AD=2,2,1$ and direction ratios of $BC=2,2,1$

$\therefore AD || BC$

So, quadrilateral $ABCD$ is a parallelogram.

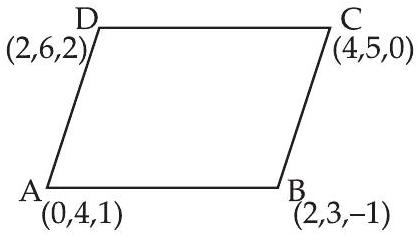
$ \begin{aligned} & \overrightarrow{{}AB}=2 \hat{i}-\hat{j}-2 \hat{k} \\ & \overrightarrow{{}AD}=2 \hat{i}+2 \hat{j}+\hat{k} \end{aligned} $

$\therefore$ Area of parallelogram $ABCD=|\overrightarrow{{}AB} \times \overrightarrow{{}AD}|$

$= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & -1 & -2 \\ 2 & 2 & 1\end{vmatrix} =\hat{i}(-1+4)-\hat{j}(2+4)+\hat{k}(4+2)=3 \hat{i}-6 \hat{j}+6 \hat{k}$

$=\sqrt{(3)^{2}+(-6)^{2}+(6)^{2}}=\sqrt{9+36+36}=\sqrt{81}=9$ sq units

Hence, the correct option is $(a)$.

Solution

Given that: $\quad x y+y z=0$

$ \begin{aligned} y \cdot(x+z) & =0 \\ y & =0 \text{ or } x+z=0 \end{aligned} $

Here $y=0$ is one plane and $x+z=0$ is another plane. So, it is a pair of planes.

To check if these planes are perpendicular, we can examine their normal vectors:

• The normal vector to the plane $ y=0 $ is $ (0,1,0) $.

• The normal vector to the plane $ x+z=0 $ is $ (1,0,1) $.

The dot product of these normal vectors is: $ (0,1,0) \cdot(1,0,1)=0 \times 1+1 \times 0+0 \times 1=0 $

Since the dot product is zero, the normals are perpendicular, which means the planes are perpendicular to each other.

Hence, the correct option is $(d)$.

• (a) A pair of perpendicular lines: The equation $xy + yz = 0$ represents a relationship in three-dimensional space involving planes, not lines. Therefore, it cannot represent a pair of perpendicular lines.

• (b) A pair of parallel lines: Similar to option (a), the equation $xy + yz = 0$ involves variables in three-dimensional space and describes planes, not lines. Hence, it cannot represent a pair of parallel lines.

• (c) A pair of parallel planes: The equation $xy + yz = 0$ simplifies to $y(x + z) = 0$, which gives two distinct planes: $y = 0$ and $x + z = 0$. These planes intersect along a line and are not parallel to each other. Therefore, it cannot represent a pair of parallel planes.

Solution

Direction ratios of the normal to the plane $2 x-3 y+6 z-11=0$ are 2, -3, 6

Direction ratios of $x$-axis are $1,0,0$

The formula for the angle between a line and a plane is given by: $ \sin \theta=\dfrac{\mathbf{d} \cdot \mathbf{n}}{|\mathbf{d}||\mathbf{n}|} $

Here:

• $ \mathbf{d} $ is the direction vector of the line.

• $ \mathbf{n} $ is the normal vector to the plane.

$ \therefore\ $ Angle between plane and line is

$ \begin{aligned} \sin \theta & =\dfrac{2(1)-3(0)+6(0)}{\sqrt{(2)^{2}+(-3)^{2}+(6^{2})} \cdot \sqrt{(1)^{2}+(0)^{2}+(0)^{2}}} \\ & =\dfrac{2}{\sqrt{4+9+36}}=\dfrac{2}{7} \end{aligned} $

Hence, the correct option is (c).

Solution

Given points are $(2,0,0),(0,3,0)$ and $(0,0,4)$.

So, the intercepts cut by the plane on the x-, y-, and z- axes are 2, 3, 4 respectively

Equation of the plane (intercept form) is

$\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1$

Here, $a$, $b$, and $c$ are the x-, y-, and z-intercepts of the plane, respectively.

$\therefore \quad \dfrac{x}{2}+\dfrac{y}{3}+\dfrac{z}{4}=1 $

Hence, the equation of plane is $\dfrac{x}{2}+\dfrac{y}{3}+\dfrac{z}{4}=1$.

Solution

Let

$ \vec{a}=2 \hat{i}+2 \hat{j}-\hat{k} $

Direction ratios of $\vec{a}$ are 2, 2, -1

The direction cosines for a vector $\vec{a} = a_1 \hat{i} + a_2 \hat{j} + a_3 \hat{k}$ are given by : $\dfrac{a_1}{\left|\vec{a}\left|\right.\right.},\dfrac{a_2}{\left|\vec{a}\right|},\dfrac{a_3}{\left|\vec{a}\right|}$

So, the direction cosines are $\dfrac{2}{\sqrt{4+4+1}}, \dfrac{2}{\sqrt{4+4+1}}, \dfrac{-1}{\sqrt{4+4+1}} \Rightarrow \dfrac{2}{3}, \dfrac{2}{3}, \dfrac{-1}{3}$

Hence, the direction cosines of the given vector are $\dfrac{2}{3}, \dfrac{2}{3}, \dfrac{-1}{3}$.

Solution

The given equation is $ \dfrac{x-5}{3}=\dfrac{y+4}{7}=\dfrac{z-6}{2} $

Here, the point $(5, -4, 6)$ represents a point on the line, which can be expressed as a position vector : $ \vec{a}=(5 \hat{i}-4 \hat{j}+6 \hat{k}) $

The direction ratios $3, 7, 2$ are used to form the equation of the line:

$ \vec{b}=(3 \hat{i}+7 \hat{j}+2 \hat{k}) $

The vector equation of the line is given by:

$ \vec{r} = \vec{a} + \lambda \vec{b} $

Hence, the vector equation of the given line is $ \vec{r}=(5 \hat{i}-4 \hat{j}+6 \hat{k})+\lambda(3 \hat{i}+7 \hat{j}+2 \hat{k}) $

Solution

Given the points $(3,4,-7)$ and $(1,-1,6)$

The point (3,4,−7) gives us a position vector : $ \vec{a} = 3 \hat{i} + 4 \hat{j} - 7 \hat{k} $

The point (1,−1,6) gives us another position vector : $ \vec{b} = \hat{i} - \hat{j} + 6 \hat{k} $

The vector equation of the line is given by :

$ \vec{r} = \vec{a} + \lambda (\vec{b} - \vec{a}) $

$\Rightarrow \vec{r}=(3 \hat{i}+4 \hat{j}-7 \hat{k})+\lambda[(\hat{i}-\hat{j}+6 \hat{k})-(3 \hat{i}+4 \hat{j}-7 \hat{k})]$

$\Rightarrow \vec{r}=(3 \hat{i}+4 \hat{j}-7 \hat{k})+\lambda(-2 \hat{i}-5 \hat{j}+13 \hat{k})$

$\Rightarrow(x \hat{i}+y \hat{j}+z \hat{k})=(3 \hat{i}+4 \hat{j}-7 \hat{k})+\lambda(-2 \hat{i}-5 \hat{j}+13 \hat{k})$

$\Rightarrow(x-3) \hat{i}+(y-4) \hat{j}+(z+7) \hat{k}=\lambda(-2 \hat{i}-5 \hat{j}+13 \hat{k})$

Hence, the vector equation of the line is

$ (x-3) \hat{i}+(y-4) \hat{j}+(z+7) \hat{k}=\lambda(-2 \hat{i}-5 \hat{j}+13 \hat{k}) $

Solution

Given equation is $\vec{r} \cdot(\hat{i}+\hat{j}-\hat{k})=2$

$\begin{matrix} \Rightarrow & (x \hat{i}+y \hat{j}+z \hat{k}) \cdot(\hat{i}+\hat{j}-\hat{k}) & =2 \\ \Rightarrow & x+y-z & =2\end{matrix} $

Hence, the Cartesian equation of the plane is $x+y-z=2$.

Solution

Given plane is $x+2 y+3 z-6=0$

Vector normal to the plane $\vec{n}=\hat{i}+2 \hat{j}+3 \hat{k}$

$\therefore \hat{n}=\dfrac{\vec{n}}{|\vec{n}|}=\dfrac{\hat{i}+2 \hat{j}+3 \hat{k}}{\sqrt{(1)^{2}+(2)^{2}+(3)^{2}}}=\dfrac{1}{\sqrt{14}} \hat{i}+\dfrac{2}{\sqrt{14}} \hat{j}+\dfrac{3}{\sqrt{14}} \hat{k}$

Hence, the given statement is ’true'.

Solution

Equation of the plane is $2 x-3 y+5 z+4=0$

$\Rightarrow \quad 2 x-3 y+5 z=-4$

$\Rightarrow \dfrac{2}{-4} x-\dfrac{3 y}{-4}+\dfrac{5 z}{-4}=1$

$\Rightarrow \dfrac{x}{-2}+\dfrac{y}{4 / 3}+\dfrac{z}{-4 / 5}=1$

So, the required intercepts are $-2, \dfrac{4}{3}$ and $-\dfrac{4}{5}$

Hence, the given statement is ’true'.

Solution

Equation of line is $\vec{r}=(5 \hat{i}-\hat{j}-4 \hat{k})+\lambda(2 \hat{i}-\hat{j}+\hat{k})$ and the equation of the plane is $\vec{r} \cdot(3 \hat{i}-4 \hat{j}-\hat{k})+5=0$

Here, direction vector of the line is: $$ \vec{b}_{1}=2 \hat{i}-\hat{j}+\hat{k} $$

Normal vector to the plane is: $$ \vec{n}_{2}=3 \hat{i}-4 \hat{j}-\hat{k} $$

The formula for the angle between a line and a plane is given by :

$ \sin \theta=\dfrac{\mathbf{d} \cdot \mathbf{n}}{|\mathbf{d}||\mathbf{n}|} $

Here:

• $ \mathbf{d} $ is the direction vector of the line.

• $ \mathbf{n} $ is the normal vector to the plane.

$\therefore \quad \sin \theta=\dfrac{b_1 \vec{n} _2}{| \vec{b} _1|| \vec{n} _2|}$

$\Rightarrow \quad \sin \theta=\dfrac{(2 \hat{i}-\hat{j}+\hat{k}) \cdot(3 \hat{i}-4 \hat{j}-\hat{k})}{\sqrt{4+1+1} \cdot \sqrt{9+16+1}}=\dfrac{6+4-1}{\sqrt{6} \cdot \sqrt{26}}=\dfrac{9}{\sqrt{6} \cdot \sqrt{26}}$

$\Rightarrow \quad \sin \theta=\dfrac{9}{2 \sqrt{39}}$

Hence, the given statement is ‘false’.

Solution

The given planes are $ \vec{r} \cdot(2 \hat{i}-3 \hat{j}+\hat{k})=1 $ and $ \vec{r} \cdot(\hat{i}-\hat{j})=4 $

Here, normal vector to the first plane is

$\vec{n}_1=2\hat{i}-3\hat{j}+\hat{k}$ and

normal vector to the second plane is

$\vec{n}_2=(\hat{i}-\hat{j})$

The cosine of the angle $ \theta $ between the two planes is given by :

$\cos\theta=\dfrac{\vec{n}_1\cdot\vec{n}_2}{|\vec{n}_1||\vec{n}_2|}$

Where, $\vec{n}_1$ and $\vec{n}_2$ are normal vectors to the planes.

So, $ \quad\cos\theta=\dfrac{(2 i-3 j+\hat{k}) \cdot(\hat{i}-\hat{j})}{\sqrt{4+9+1} \cdot\sqrt{1+1}}=\dfrac{2+3}{\sqrt{14} \cdot\sqrt{2}}=\dfrac{5}{\sqrt{28}} $

$ \therefore \quad \theta=\cos ^{-1}\left(\dfrac{5}{\sqrt{28}}\right) $

Hence, the given statement is ‘false’.

Solution

Direction vector of the given Line is : $ \vec{d} = \hat{i} - \hat{j} + 2 \hat{k} $

Normal vector to the given Plane is : $ \vec{n} = 3 \hat{i} + \hat{j} - \hat{k} $

Checking Parallelism:

For the line to be parallel to the plane, the direction vector of the line should be perpendicular to the normal vector of the plane.

This means their dot product should equal zero:

$ \vec{d} \cdot \vec{n} = (\hat{i} - \hat{j} + 2 \hat{k}) \cdot (3 \hat{i} + \hat{j} - \hat{k}) = 1 \cdot 3 + (-1) \cdot 1 + 2 \cdot (-1) = 3 - 1 - 2 = 0 $

Since the dot product is zero, the line is indeed parallel to the plane.

Checking if the Line Lies in the Plane:

For the line to lie in the plane, a point on the line should satisfy the equation of the plane.

The position vector of the point through which the line passes is : $ \vec{a} = 2 \hat{i} - 3 \hat{j} - \hat{k} $

Substitute $\vec{a}$ into the plane equation : $ (2 \hat{i} - 3 \hat{j} - \hat{k}) \cdot (3 \hat{i} + \hat{j} - \hat{k}) + 2 = 6 - 3 + 1 + 2 = 6 $

The result is not zero, so the point does not satisfy the plane’s equation.

Therefore, the line does not lie in the plane.

Hence, the given statement is ‘false’.

Solution

The given Cartesian form of the line is : $ \dfrac{x-5}{3} = \dfrac{y+4}{7} = \dfrac{z-6}{2} = \lambda $

This equation describes a line passing through the point $(x_1, y_1, z_1) = (5, -4, 6)$ with the direction ratios $ (a, b, c) = (3, 7, 2) $.

To convert the Cartesian form to vector form, we use the point and the direction vector:

The position vector is given by :

$ \vec{r}_0 = 5 \hat{i} - 4 \hat{j} + 6 \hat{k} $

The direction vector is:

$ \vec{d} = 3 \hat{i} + 7 \hat{j} + 2 \hat{k} $

The vector equation of the line is then :

$\vec{r}=\vec{r}_0+\lambda\vec{d}$

$ \Rightarrow \vec{r} = (5 \hat{i} - 4 \hat{j} + 6 \hat{k}) + \lambda (3 \hat{i} + 7 \hat{j} + 2 \hat{k}) $

Hence, the given statement is ’true'.

Solution

The equation of line in Cartesian form is given by : $ \dfrac{x - x_1}{a} = \dfrac{y - y_1}{b} = \dfrac{z - z_1}{c} $

where $ (x_1, y_1, z_1) $ is the point the line passes through and $ (a, b, c) $ are the direction ratios.

Given:

• Point through which the line passes : $ (5, -2, 4) $

• Line parallel to the vector : $ 2 \hat{i} + \hat{j} + 3 \hat{k} $

Hence, $ x_1 = 5, y_1 = -2, z_1 = 4 $ and $ a = 2, b = 1, c = 3 $

Thus, the equation of line should be : $ \dfrac{x - 5}{2} = \dfrac{y + 2}{1} = \dfrac{z - 4}{3} $

Hence, the given statement is ‘false’.

Solution

The equation of a plane with a normal vector $\vec{n} = (a, b, c)$ passing through a point $(x_0, y_0, z_0)$ is :

$ a(x - x_0) + b(y - y_0) + c(z - z_0) = 0 $

• The foot of the perpendicular from the origin to a plane provides a point $(x_0, y_0, z_0)$ that lies on the plane.

• The normal vector of the plane is the same as the vector connecting the origin to this point $(x_0,y_0,z_0)$.

Therefore, $\vec{n}=(x_0,y_0,z_0)$.

Equation of plane when foot of the perpendicular from the origin is $(x_0,y_0,z_0)$:

$x_0(x-x_0)+y_0(y-y_0)+z_0(z-z_0)=0$

Since the foot of the perpendicular is $(5, -3, -2)$, the equation of the plane is:

$5(x-5)-3(y+3)-2(z+2)=0$

$\Rightarrow5x-3y-2z=38$

$\Rightarrow\vec{r}\cdot(5\hat{i}-3\hat{j}-2\hat{k})=38$

Hence, the given statement is ’true'.