Answer :

(i): The given equation is $x+7 y=0$

It can be written as

$y=-\dfrac{1}{7} x+0\qquad\ldots (1)$

This equation is of the form $y=m x+c$, where

$ m=-\dfrac{1}{7} \text{ and } c=0 $

Therefore, equation $(1)$ is in the slope-intercept form, where the slope and the $y$-intercept are $-\dfrac{1}{7}$ and $0$ respectively.

(ii): The given equation is $6 x+3 y -5=0$

It can be written as

$y=\dfrac{1}{3}(-6 x+5)$

$y=-2 x+\dfrac{5}{3}\qquad\ldots (2)$

This equation is of the form $y=m x+c$, where $m=-2$ and $c=\dfrac{5}{3}$

Therefore, equation $(2)$ is in the slope-intercept form, where the slope and the $y$-intercept are- $2$ and $\dfrac{5}{3}$ respectively.

(iii): The given equation is $y=0$.

It can be written as

$y=0 . x+0 \qquad\ldots (3)$

This equation is of the form $y=m x+c$, where $m=0$ and $c=0$.

Therefore, equation $(3)$ is in the slope-intercept form, where the slope and the $y$-intercept are $0$ and $0$ respectively.

Answer :

(i): The given equation is $3 x+2 y- 12=0$

It can be written as

$3 x+2 y=12$

$\dfrac{3 x}{12}+\dfrac{2 y}{12}=1$

i.e., $ \quad \dfrac{x}{4}+\dfrac{y}{6}=1\qquad\ldots (1)$

This equation is of the form $\dfrac{x}{a}+\dfrac{y}{b}=1$, where $a=4$ and $b=6$.

Therefore, equation $(1)$ is in the intercept form, where the intercepts on the $x$ and $y$ axes are $4$ and $6$ respectively.

(ii): The given equation is $4 x - 3 y=6$.

It can be written as

$\dfrac{4 x}{6}-\dfrac{3 y}{6}=1$

$\dfrac{2 x}{3}-\dfrac{y}{2}=1$

i.e., $ \quad \dfrac{x}{(\frac{3}{2})}+\dfrac{y}{(-2)}=1\qquad\ldots (2)$

This equation is of the form $\dfrac{x}{a}+\dfrac{y}{b}=1$, where $a=\dfrac{3}{2}$ and $b=-2$ .

Therefore, equation $(2)$ is in the intercept form, where the intercepts on the $x$ and $y$ axes are $\dfrac{3}{2}$ and $-2$ respectively.

(iii): The given equation is $3 y+2=0$.

It can be written as $3 y=-2$

i.e., $\dfrac{y}{\left(-\dfrac{2}{3}\right)}=1\qquad\ldots (3)$

This equation is of the form $\dfrac{x}{a}+\dfrac{y}{b}=1$, where $a=0$ and $b=-\dfrac{2}{3}$.

Therefore, equation $(3)$ is in the intercept form, where the intercept on the $y$-axis is $-\dfrac{2}{3}$ and it has no intercept on the $x$-axis.

Answer :

The given equation of the line is $12(x+6)=5(y - 2)$

$\Rightarrow 12 x+72=5 y - 10$

$\Rightarrow 12 x - 5 y+82=0$

On comparing equation $(1)$ with general equation of line $A x+B y+C=0$, we obtain $A=12, B= - 5$ , and $C=82$.

It is known that the perpendicular distance $( d )$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by

$d=\dfrac{\big|A x_1+B y_1+C\big|}{\sqrt{A^{2}+B^{2}}}$.

The given point is $(x_1, y_1)=(- 1,1)$.

Therefore, the distance of point $( - 1,1 )$ from the given line

$=\dfrac{\big|12(-1)+(-5)(1)+82\big|}{\sqrt{(12)^{2}+(-5)^{2}}}$ units $=\dfrac{\big|-12-5+82\big|}{\sqrt{169}}$ units $=\dfrac{\big|65\big|}{13}$ units $=5$ units

Answer :

The given equation of line is $\dfrac{x}{3}+\dfrac{y}{4}=1$

or, $4 x+3 y-12=0$

On comparing equation $(1)$ with general equation of line $A x+B y+C=0$, we obtain $A=4, \ B=3$, and $C= - 12$

Let $(a, 0)$ be the point on the $x$-axis whose distance from the given line is $4$ units.

It is known that the perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by

$d=\dfrac{\big|A x_1+B y_1+C\big|}{\sqrt{A^{2}+B^{2}}}$

Therefore,

$ \quad 4=\dfrac{\big|4 a+3 \times 0-12\big|}{\sqrt{4^{2}+3^{2}}}$

$\Rightarrow 4=\dfrac{\big|4 a-12\big|}{5}$

$\Rightarrow\big|4 a-12\big|=20$

$\Rightarrow \pm(4 a-12)=20$

$\Rightarrow(4 a-12)=20$ or $-(4 a-12)=20$

$\Rightarrow 4 a=20+12$ or $4 a=-20+12$

$\Rightarrow a=8$ or $-2$

Thus, the required points on the $x$-axis are $(-2,0)$ and $(8,0)$.

Answer :

It is known that the distance $(d)$ between parallel lines $A x+B y+C_1=0$ and $A x+B y+C_2=0$ is given by $d=\dfrac{\big|C_1-C_2\big|}{\sqrt{A^{2}+B^{2}}}$

(i): The given parallel lines are $15 x+8 y - 34=0$ and $15 x+8 y+31=0$

Here, $A=15, \ B=8, \ C_1= - 34 ,$ and $C_2=31$.

Therefore, the distance between the parallel lines is $d=\dfrac{\big|C_1-C_2\big|}{\sqrt{A^{2}+B^{2}}}=\dfrac{\big|-34-31\big|}{\sqrt{(15)^{2}+(8)^{2}}}$ $=\dfrac{\big|-65\big|}{17}$ $=\dfrac{65}{17}$ units

(ii): The given parallel lines are $l(x+y)+p=0$ and $l(x+y) - r=0$.

$l x+l y+p=0$ and $l x+l y - r=0$

Here,

$A=l, \ B=l, \ C_1=p$, and $C_2=- r$.

Therefore, the distance between the parallel lines is

$d=\dfrac{\big|C_1-C_2\big|}{\sqrt{A^{2}+B^{2}}}=\dfrac{\big|p+r\big|}{\sqrt{l^{2}+l^{2}}}$ $=\dfrac{\big|p+r\big|}{\sqrt{2 l^{2}}}$ $=\dfrac{\big|p+r\big|}{l \sqrt{2}}$ $=\dfrac{1}{\sqrt{2}}\big|\dfrac{p+r}{l}\big|$ units

Answer :

The equation of the given line is

$3 x-4 y+2=0$

or $y=\dfrac{3 x}{4}+\dfrac{2}{4}$

or $y=\dfrac{3}{4} x+\dfrac{1}{2}$, which is of the form $y=m x+c$

$\therefore \ \ $ Slope of the given line $ =\dfrac{3}{4} $

It is known that parallel lines have the same slope.

$\therefore$ Slope of the other line $ m=\dfrac{3}{4} $

Now, the equation of the line that has a slope of $\dfrac{3}{4}$ and passes through the point $(-2,3)$ is

$ \begin{aligned} & (y-3)=\dfrac{3}{4}\lbrace x-(-2) \rbrace \\ \\ & 4 y-12=3 x+6 \\ \\ & \text{ i.e., } 3 x-4 y+18=0 \end{aligned} $

Answer :

The given equation of line is $x-7 y+5=0$

Or, $ \ y=\dfrac{1}{7} x+\dfrac{5}{7}$, which is of the form $y=m x+c$

$\therefore \ \ $ Slope of the given line $ =\dfrac{1}{7} $

The slope of the line perpendicular to the line having a slope of $\dfrac{1}{7}$ is $m=-\dfrac{1}{\left(\frac{1}{7}\right)}=-7$

The equation of the line with slope $- 7$ and $x$-intercept 3 is given by

$\quad y=m(x - d)$

$\Rightarrow y=- 7(x - 3)$

$\Rightarrow y=- 7 x+21$

$\Rightarrow 7 x+y=21$

Answer :

The given lines are $\sqrt{3} x+y=1$ and $x+\sqrt{3} y=1$.

$y=-\sqrt{3} x+1 \qquad \ldots(1) \quad$

and $y=-\dfrac{1}{\sqrt{3}} x+\dfrac{1}{\sqrt{3}}\qquad\ldots\mathrm{(2)}$

The slope of line $(1)$ is $m_1=-\sqrt{3}$, while the slope of line $(2)$ is $m_2=-\dfrac{1}{\sqrt{3}}$

The acute angle i.e., $\theta$ between the two lines is given by $\tan \theta=\left|\dfrac{m_1-m_2}{1+m_1 m_2}\right|$

$\tan \theta=\left|\dfrac{-\sqrt{3}+\dfrac{1}{\sqrt{3}}}{1+(-\sqrt{3})(-\dfrac{1}{\sqrt{3}})}\right|$

$\tan \theta=\left|\dfrac{\dfrac{-3+1}{\sqrt{3}}}{1+1}\right|=\left|\dfrac{-2}{2 \times \sqrt{3}}\right|$

$\tan \theta=\dfrac{1}{\sqrt{3}}$

$\quad \ \theta=30^{\circ}$

Thus, the angle between the given lines is either $30^{\circ}$ or $180^{\circ} - 30^{\circ}=150^{\circ}$

Answer :

The slope of the line passing through points $(h, 3)$ and $(4,1)$ is $m_1=\dfrac{1-3}{4-h}=\dfrac{-2}{4-h}$

The slope of line $7 x$ - $9 y$ - $19=0$ or $y=\dfrac{7}{9} x-\dfrac{19}{9} \quad m_2=\dfrac{7}{9}$

It is given that the two lines are perpendicular.

$\therefore \ m_1 \times m_2=-1$

$\Rightarrow \left(\dfrac{-2}{4-h}\right) \times\left(\dfrac{7}{9}\right)=-1$

$\Rightarrow \dfrac{-14}{36-9 h}=-1$

$\Rightarrow 14=36-9 h$

$\Rightarrow 9 h=36-14$

$\Rightarrow h=\dfrac{22}{9}$

Thus, the value of $h$ is $\dfrac{22}{9}$

Answer :

The slope of line $A x+B y+C=0$ or $y=\left(\dfrac{-A}{B}\right) x+\left(\dfrac{-C}{B}\right)$ is $\quad m=-\dfrac{A}{B}$

It is known that parallel lines have the same slope.

$\therefore \ \ $ Slope of the other line $ ~ m=-\dfrac{A}{B}$

The equation of the line passing through point $(x_1, y_1)$ and having a slope $m=-\dfrac{A}{B}$ is

$y-y_1=m(x-x_1)$

$y-y_1=-\dfrac{A}{B}(x-x_1)$

$B(y-y_1)=-A(x-x_1)$

$A(x-x_1)+B(y-y_1)=0$

Hence, the line through point $(x_1, y_1)$ and parallel to line $A x+B y+C=0$ is

$A(x - x_1)+B(y - y_1)=0$

Answer :

It is given that the slope of the first line, $m_1=2$.

Let the slope of the other line be $m_2$.

The angle between the two lines is $60^{\circ}$.

$\therefore \ \tan 60^{\circ}=\left|\dfrac{m_1-m_2}{1+m_1 m_2}\right|$

$\Rightarrow \sqrt{3}=\left|\dfrac{2-m_2}{1+2 m_2}\right|$

$\Rightarrow \sqrt{3}= \pm\left(\dfrac{2-m_2}{1+2 m_2}\right)$

$\Rightarrow \sqrt{3}=\dfrac{2-m_2}{1+2 m_2}$ or $\sqrt{3}=-\left(\dfrac{2-m_2}{1+2 m_2}\right)$

$\Rightarrow \sqrt{3}(1+2 m_2)=2-m_2$ or $\sqrt{3}(1+2 m_2)=-(2-m_2)$

$\Rightarrow \sqrt{3}+2 \sqrt{3} m_2+m_2=2$ or $\sqrt{3}+2 \sqrt{3} m_2-m_2=-2$

$\Rightarrow \sqrt{3}+(2 \sqrt{3}+1) m_2=2$ or $\sqrt{3}+(2 \sqrt{3}-1) m_2=-2$

$\Rightarrow m_2=\dfrac{2-\sqrt{3}}{(2 \sqrt{3}+1)}$ or $m_2=\dfrac{-(2+\sqrt{3})}{(2 \sqrt{3}-1)}$

Case I: $\quad m_2=\left(\dfrac{2-\sqrt{3}}{2 \sqrt{3}+1}\right)$

The equation of the line passing through point $(2,3)$ and having a slope of $\left(\dfrac{2-\sqrt{3}}{2 \sqrt{3}+1}\right)$ is

$(y-3)=\dfrac{2-\sqrt{3}}{2 \sqrt{3}+1}(x-2)$

$(2 \sqrt{3}+1) y-3(2 \sqrt{3}+1)=(2-\sqrt{3}) x-2(2-\sqrt{3})$

$(\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-4+2 \sqrt{3}+6 \sqrt{3}+3$

$(\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-1+8 \sqrt{3}$

In this case, the equation of the other line is $(\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-1+8 \sqrt{3}$.

Case II : $\quad m_2= -\left(\dfrac{2+\sqrt{3}}{2 \sqrt{3}-1}\right)$

The equation of the line passing through point $(2,3)$ and having a slope of $-\left(\dfrac{2+\sqrt{3}}{2 \sqrt{3}-1}\right)$ is

$ \begin{aligned} & (y-3)=-\left(\dfrac{2+\sqrt{3}}{2 \sqrt{3}-1}\right)(x-2) \\ \\ & (2 \sqrt{3}-1) y-3(2 \sqrt{3}-1)=-(2+\sqrt{3}) x+2(2+\sqrt{3}) \\ \\ & (2 \sqrt{3}-1) y+(2+\sqrt{3}) x=4+2 \sqrt{3}+6 \sqrt{3}-3 \\ \\ & (2+\sqrt{3}) x+(2 \sqrt{3}-1) y=1+8 \sqrt{3} \end{aligned} $

In this case, the equation of the other line is $(2+\sqrt{3}) x+(2 \sqrt{3}-1) y=1+8 \sqrt{3}$.

Thus, the required equation of the other line is $(\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-1+8 \sqrt{3}$

or $(2+\sqrt{3}) x+(2 \sqrt{3}-1) y=1+8 \sqrt{3}$

Answer :

The right bisector of a line segment bisects the line segment at $90^{\circ}$.

The end-points of the line segment are given as $A (3,4)$ and $B(-{ } 1,2)$.

Accordingly, mid-point of $A B$ $ =\left(\dfrac{3-1}{2}, \dfrac{4+2}{2}\right)=(1,3) $

Slope of $A B=\left(\dfrac{2-4}{-1-3}\right)=\left(\dfrac{-2}{-4}\right)=\dfrac{1}{2}$

$\therefore \ $ Slope of the line perpendicular to $A B$ $ =-\dfrac{1}{\left(\dfrac{1}{2}\right)}=-2 $

The equation of the line passing through $(1,3)$ and having a slope of $- 2$ is

$(y - 3)= -2 (x - 1)$

$y - 3=- 2 x+2$

$2 x+y=5$

Thus, the required equation of the line is $2 x+y=5$.

Answer :

Let $(a, b)$ be the coordinates of the foot of the perpendicular from the point $(- 1,3)$ to the line $3 x - 4 y - 16=0$.

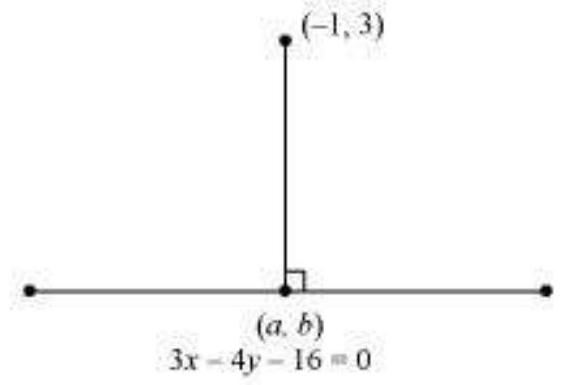
Slope of the line joining $( - 1,3) \text{ and } (a, b), m_1=\dfrac{b-3}{a+1}$

Slope of the line $3 x$- $4 y$- $16=0$ or $y=\dfrac{3}{4} x-4, m_2=\dfrac{3}{4}$

Since these two lines are perpendicular, $m_1 m_2= - 1$

$\therefore\left(\dfrac{b-3}{a+1}\right) \times\left(\dfrac{3}{4}\right)=-1$

$\Rightarrow \dfrac{3 b-9}{4 a+4}=-1$

$\Rightarrow 3 b-9=-4 a-4$

$\Rightarrow 4 a+3 b=5\qquad\ldots\mathrm{(1)}$

Point $(a, b)$ lies on line $3 x$ - $4 y=16$.

$\therefore \ \ 3 a$ - $4 b=16\qquad\ldots\mathrm{(2)}$

On solving equations $(1)$ and $(2),$ we obtain

$a=\dfrac{68}{25}$ and $b=-\dfrac{49}{25}$

Thus, the required coordinates of the foot of the perpendicular are $\left(\dfrac{68}{25},-\dfrac{49}{25}\right)$

Answer :

The given equation of line is $y=m x+c$.

It is given that the perpendicular from the origin meets the given line at $(-1,2).$

Therefore, the line joining the points $(0,0)$ and $(- 1,2)$ is perpendicular to the given line.

$\therefore \ $ Slope of the line joining $(0,0)$ and $( - 1,2)$ $ =\dfrac{2}{-1}=-2 $

The slope of the given line is $m$.

$\therefore \ \ m \times -2=-1 \qquad $ [The two lines are perpendicular]

$\Rightarrow m=\dfrac{1}{2}$

Since point $( - 1,2)$ lies on the given line, it satisfies the equation $y=m x+c$.

$\therefore 2=m(-1)+c$

$\Rightarrow 2=\dfrac{1}{2}(-1)+c$

$\Rightarrow c=2+\dfrac{1}{2}=\dfrac{5}{2}$

Thus, the respective values of $m$ and $c$ are $\dfrac{1}{2}$ and $\dfrac{5}{2}$.

Answer :

The equations of given lines are

$x \cos \theta - y \sin \theta=k \cos 2 \theta \qquad\ldots\mathrm{(1)}$

$x \sec \theta+y cosec \theta=k$.

The perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by

$ d=\dfrac{\big|A x_1+B y_1+C\big|}{\sqrt{A^{2}+B^{2}}} \qquad \ldots {(2)} $

On comparing equation $(1)$ to the general equation of line i.e., $A x+B y+C=0$, we obtain $A=\cos \theta, \ B= -\sin \theta$, and $C=- k \cos 2 \theta$.

It is given that $p$ is the length of the perpendicular from $(0,0)$ to line $(1)$.

$\therefore \ \ p=\dfrac{\big|A(0)+B(0)+C\big|}{\sqrt{A^{2}+B^{2}}}=\dfrac{\big|C\big|}{\sqrt{A^{2}+B^{2}}}=\dfrac{\big|-k \cos 2 \theta\big|}{\sqrt{\cos ^{2} \theta+\sin ^{2} \theta}}=\big|-k \cos 2 \theta\big|$

On comparing equation $(2)$ to the general equation of line i.e., $A x+B y+C=0$, we obtain $A=\sec \theta, \ B=cosec \theta$, and $C= -k.$

It is given that $q$ is the length of the perpendicular from $(0,0)$ to line $(2).$

$\therefore \quad q=\dfrac{\big|A(0)+B(0)+C\big|}{\sqrt{A^{2}+B^{2}}}=\dfrac{\big|C\big|}{\sqrt{A^{2}+B^{2}}}=\dfrac{\big|-k\big|}{\sqrt{\sec ^{2} \theta+cosec^{2} \theta}}$

From $(3)$ and $(4),$ we have

$ \begin{aligned} p^{2}+4 q^{2} & =(-k \cos 2 \theta)^{2}+4\left(\dfrac{\big|-k\big|}{\sqrt{\sec ^{2} \theta+cosec^{2} \theta}}\right)^{2} \\ \\ & =k^{2} \cos ^{2} 2 \theta+\dfrac{4 k^{2}}{(\sec ^{2} \theta+cosec^{2} \theta)} \\ \\ & =k^{2} \cos ^{2} 2 \theta+\dfrac{4 k^{2}}{\left(\dfrac{1}{\cos ^{2} \theta}+\dfrac{1}{\sin ^{2} \theta}\right)} \\ \\ & =k^{2} \cos ^{2} 2 \theta+\dfrac{4 k^{2}}{\left(\dfrac{\sin ^{2} \theta+\cos ^{2} \theta}{\sin ^{2} \theta \cos ^{2} \theta}\right)} \\ \\ & =k^{2} \cos ^{2} 2 \theta+\dfrac{4 k^{2}}{\left(\dfrac{1}{\sin ^{2} \theta \cos ^{2} \theta}\right)} \\ \\ & =k^{2} \cos ^{2} 2 \theta+4 k^{2} \sin ^{2} \theta \cos ^{2} \theta \\ \\ & =k^{2} \cos ^{2} 2 \theta+k^{2}(2 \sin \theta \cos \theta)^{2} \\ \\ & =k^{2} \cos ^{2} 2 \theta+k^{2} \sin ^{2} 2 \theta \\ \\ & =k^{2}(\cos ^{2} 2 \theta+\sin ^{2} 2 \theta) \\ \\ & =k^{2} \end{aligned} $

Hence, we proved that $p^{2}+4 q^{2}=k^{2}$.

Answer :

Let $A D$ be the altitude of triangle $A B C$ from vertex $A$.

Accordingly, $A D \perp B C$

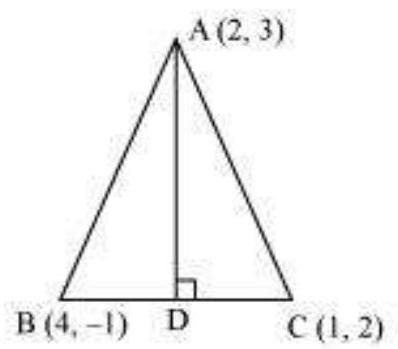
The equation of the line passing through point $(2,3)$ and having a slope of 1 is

$(y - 3)=1(x -2 )$

$\Rightarrow x - y+1=0$

$\Rightarrow y - x=1$

Therefore, equation of the altitude from vertex A

$y - x=1$

Length of $A D=$ Length of the perpendicular from $A(2,3)$ to $B C$

The equation of $B C$ is

$(y+1)=\left(\dfrac{2+1}{1-4}\right)(x-4)$

$\Rightarrow(y+1)=-1(x-4)$

$\Rightarrow y+1=-x+4$

$\Rightarrow x+y-3=0$

The perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by $\sqrt{A^{2}+B^{2}}$.

On comparing equation $(1)$ to the general equation of line $A x+B y+C=0$, we obtain $A=1, B=1$, and $C= - 3 .$

$\therefore \ \ $ Length of $A D$ $ =\dfrac{\big|1 \times 2+1 \times 3-3\big|}{\sqrt{1^{2}+1^{2}}} =\dfrac{\big|2\big|}{\sqrt{2}} =\dfrac{2}{\sqrt{2}} =\sqrt{2} \text{ units } $

Thus, the equation and the length of the altitude from vertex $A$ are $y -$ $x=1$ and $\sqrt{2}$ units respectively.

Answer :

It is known that the equation of a line whose intercepts on the axes are $a$ and $b$ is $\dfrac{x}{a}+\dfrac{y}{b}=1 $

$\text{ or } ~ b x+a y-a b=0 \qquad \ldots {(1)}$

The perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $(x_1, y_1)$ is given by

$ d=\dfrac{\big|A x_1+B y_1+C\big|}{\sqrt{A^{2}+B^{2}}} $

On comparing equation $(1)$ to the general equation of line $A x+B y+C=0$, we obtain $A=b, \ B=a$, and $C=a -a b$.

Therefore, if $p$ is the length of the perpendicular from point $(x_1, y_1)=(0,0)$ to line $(1),$ we obtain

$p=\dfrac{\big|A(0)+B(0)-a b\big|}{\sqrt{b^{2}+a^{2}}}$

$\Rightarrow p=\dfrac{\big|-a b\big|}{\sqrt{a^{2}+b^{2}}}$

On squaring both sides, we obtain

$p^{2}=\dfrac{(-a b)^{2}}{a^{2}+b^{2}}$

$\Rightarrow p^{2}(a^{2}+b^{2})=a^{2} b^{2}$

$\Rightarrow \dfrac{a^{2}+b^{2}}{a^{2} b^{2}}=\dfrac{1}{p^{2}}$

$\Rightarrow \dfrac{1}{p^{2}}=\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}$

Hence, we showed that $\dfrac{1}{p^{2}}=\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}$