Lines and Angles
Multiple Choice Questions(MCQs)
1. In Fig., if $A B||C D|| E F, P Q || R S, \angle R Q D=25^{\circ}$ and $\angle C Q P=60^{\circ}$, then $\angle QRS$ is equal to
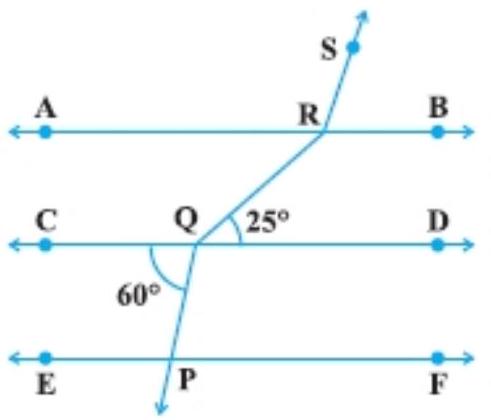
(A) $85^{\circ}$
(B) $135^{\circ}$
(C) $145^{\circ}$
(D) $110^{\circ}$
Show Answer
Solution
As $\angle A R Q=\angle R Q D=25^{\circ}$ [alt. $\angle s$ ]
Also, $\angle R Q C=180^{\circ}-60^{\circ}=120^{\circ}$ (linear pair)
And, $\angle S R A=120^{\circ}$ (Corresponding angle)
Now,
$\angle S R Q=120^{\circ}+25^{\circ}$
$\angle S R Q=145^{\circ}$
Hence, the correct option is (C).
2. If one angle of a triangle is equal to the sum of the other two angles, then the triangle is
(A) an isosceles triangle
(B) an obtuse triangle
(C) an equilateral triangle
(D) a right triangle
Show Answer
Solution
Let angle of triangle $ABC$ be $\angle A, \angle B$ and $\angle C$
Given that:
$\angle A=\angle B+\angle C$
We know that in any triangle $\angle A+\angle B+\angle C=180^{\circ}$
From equation (I) and (II), get:
$\angle A+\angle A=180^{\circ}$
$ \begin{aligned} 2 \angle A & =180^{\circ} \\ \angle A & =\dfrac{180^{\circ}}{2} \\ \angle A & =90^{\circ} \end{aligned} $
Hence, the triangle is a right triangle.
Therefore, the correct option is (D).
3. An exterior angle of a triangle is $105^{\circ}$ and its two interior opposite angles are equal. Each of these equal angles is
(A) $37 \dfrac{1}{2}^{\circ}$
(B) $52 \dfrac{1}2^{\circ}$
(C) $72 \dfrac{1}{2}^{\circ}$
(D) $75^{\circ}$
Show Answer
Solution
Given: An exterior angle of triangle is $150^{\circ}$.
Let each of the two interior opposite angle be $x$.
The sum of two interior opposite angle is equal to exterior angle of a triangle.
$ \begin{aligned} 105^{\circ} & =x+x \\ 2 x & =105^{\circ} \\ x & =52 \dfrac{1}2^{\circ} \end{aligned} $
So, each of equal angle is $\quad 52 \dfrac{1}2^{\circ}$
Hence, the correct option is (B).
4. The angles of a triangle are in the ratio $5: 3: 7$. The triangle is
(A) an acute angled triangle
(B) an obtuse angled triangle
(C) a right triangle
(D) an isosceles triangle
Show Answer
Solution
Let the angle of the triangle are $5 x, 3 x$ and $7 x$. As we know that sum of all angle of triangle is $180^{\circ}$. Now,
$5 x+3 x+7 x=180^{\circ}$
$ \begin{aligned} 15 x & =180^{\circ} \\ x & =\dfrac{180^{\circ}}{15} \\ x & =12^{\circ} \end{aligned} $
Hence, the angle of the triangle are:
$5 \times 12^{\circ}=60^{\circ}$
$3 \times 12^{\circ}=36^{\circ}$
$7 \times 12^{\circ}=84^{\circ}$
All the angle of this triangle is less than 90 degree.
Hence, the triangle is an acute angled triangle.
5. If one of the angles of a triangle is $130^{\circ}$, then the angle between the bisectors of the other two angles can be
(A) $50^{\circ}$
(B) $65^{\circ}$
(C) $145^{\circ}$
(D) $155^{\circ}$
Show Answer
Solution
In triangle $ABC$, Let $\angle A=130^{\circ}$.
The bisector of the angle $B$ and $C$ are $OB$ and $OC$.
Let $\angle O B C=\angle O B A=x$ and $\angle O C B=\angle O C A=y$
In triangle $ABC$,
$ \begin{aligned} \angle A+\angle B+\angle C & =180^{\circ} \\ 130^{\circ}+2 x+2 y & =180^{\circ} \\ 2 x+2 y & =180^{\circ}-130^{\circ} \\ 2 x+2 y & =50^{\circ} \\ x+y & =25^{\circ} \end{aligned} $
That is $\angle O B C+\angle O C A=25^{\circ}$
Now, in triangle BOC:
$ \begin{aligned} \angle B O C & =180^{\circ}-(\angle O B C+\angle O C B) \\ & =180^{\circ}-25^{\circ} \\ & =155^{\circ} \end{aligned} $
Hence, the correct option is (D).
6. In Fig., $POQ$ is a line. The value of $x$ is
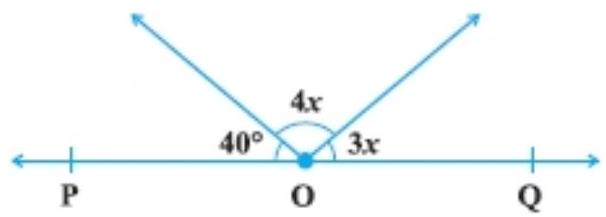
(A) $20^{\circ}$
(B) $25^{\circ}$
(C) $30^{\circ}$
(D) $35^{\circ}$
Show Answer
Solution
See the given figure in the question:
$ \begin{gathered} 40^{\circ}+4 x+3 x=180^{\circ} \text{ (Angles on the straight line) } \\ 4 x+3 x=180^{\circ}-40^{\circ} \\ 7 x=140^{\circ} \\ x=\dfrac{140^{\circ}}{7} \\ x=20^{\circ} \end{gathered} $
Hence, the correct option is (A).
7. In Fig., if $OP || RS, \angle OPQ=110^{\circ}$ and $\angle QRS=130^{\circ}$, then $\angle PQR$ is equal to
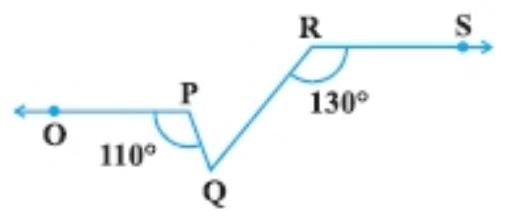
(A) $40^{\circ}$
(B) $50^{\circ}$
(C) $60^{\circ}$
(D) $70^{\circ}$
Show Answer
Solution
See the given figure, producing OP, to intersect RQ at X.
Given: $OP || RS$ and $RX$ is a transversal.
So, $\angle R X P=\angle X R S$ (alternative angle)
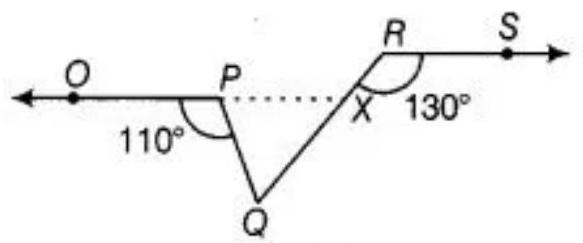
$\angle R X P=130^{\circ}$ [Given: $\angle Q R S=130^{\circ}$ ]
$RQ$ is a line segment.
So, $\angle P X Q+\angle R X V=180^{\circ}$ [linear pair axiom]
$\angle P X Q=180^{\circ}-\angle R X P=180^{\circ}-130^{\circ}$
$\angle P X Q=50^{\circ}$
In triangle $PQX, \angle O P Q$ is an exterior angle,
Therefore, $\angle O P Q=\angle P X Q+\angle P Q X$ [exterior angle = sum of two opposite interior angles]
$110^{\circ}=50^{\circ}+\angle P Q X$
$\angle P Q X=110^{\circ}-50^{\circ}$
$\angle P Q R=60^{\circ}$
Hence, the correct option is (
8. Angles of a triangle are in the ratio $2: 4: 3$. The smallest angle of the triangle is
(A) $60^{\circ}$
(B) $40^{\circ}$
(C) $80^{\circ}$
(D) $20^{\circ}$
Show Answer
Solution
Given, the ratio of angles of a triangle is $2: 4: 3$.
Let the angles of a triangle be $\angle A, \angle B$ and $\angle C$.
$\angle A=2 x, \angle B=4 x \angle C=3 x$,
$\angle A+\angle B+\angle C=180^{\circ}$ [sum of all the angles of a triangle is $180^{\circ}$ ]
$2 x+4 x+3 x=180^{\circ}$
$9 x=180^{\circ}$
$x=180^{\circ} / 9$
$=20^{\circ}$
$\angle A=2 x=2 \times 20^{\circ}=40^{\circ}$
$\angle B=4 x=4 x 20^{\circ}=80^{\circ}$
$\angle C=3 x=3 \times 20^{\circ}=60^{\circ}$
So, the smallest angle of a triangle is $40^{\circ}$.
Hence, the correct option is (B).
Short Answer Questions with Reasoning
1. For what value of $x+y$ in Fig. will $A B C$ be a line? Justify your answer.
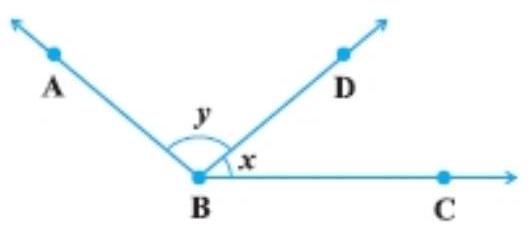
Show Answer
Solution
See the figure, $x$ and $y$ are two adjacent angles.
For $ABC$ to be a straight line, the sum of two adjacent angle must be $180^{\circ}$.
2. Can a triangle have all angles less than $60^{\circ}$ ? Give reason for your answer.
Show Answer
Solution
We know that in a triangle, sum of all the angles is always $180^{\circ}$. So, a triangle can’t have all angles less than $60^{\circ}$.
3. Can a triangle have two obtuse angles? Give reason for your answer.
Show Answer
Solution
If an angle whose measure is more than $90^{\circ}$ but less than $180^{\circ}$ is called an obtuse angle.
We know that a triangle can’t have two obtuse angle because the sum of all the angles of it can’t be more than $180^{\circ}$. It is always equal to $180^{\circ}$.
4. How many triangles can be drawn having its angles as $45^{\circ}, 64^{\circ}$ and $72^{\circ}$ ? Give reason for your answer.
Show Answer
Solution
We know that sum of all the angles in a triangle is $180^{\circ}$.
The sum of all the angles is $45^{\circ}+64^{\circ}+72^{\circ}=181^{\circ}$. So, we can’t draw any triangle having sum of all the angle $181^{\circ}$.
5. How many triangles can be drawn having its angles as $53^{\circ}, 64^{\circ}$ and $63^{\circ}$ ? Give reason for your answer.
Show Answer
Solution
We know that sum of all the angles in a triangle is $180^{\circ}$.
Sum of these angles $=53^{\circ}+64^{\circ}+63^{\circ}=180^{\circ}$. So, we can draw infinitely many triangles having its angles as $53^{\circ}, 64^{\circ}$ and $63^{\circ}$.
6. In Fig., find the value of $x$ for which the lines $l$ and $m$ are parallel.
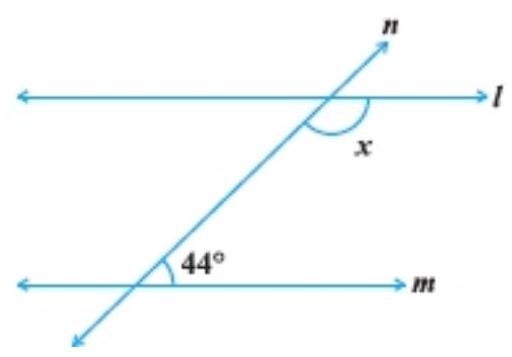
Show Answer
Solution
See the given figure, $l \text{ and } m$ if a transversal intersects two parallel lines, then sum of interior angles on the same side of a transversal is supplementary.
$x+44^{\circ}=180^{\circ}$
$ \begin{aligned} & x=180^{\circ}-44^{\circ} \\ & x=136^{\circ} \end{aligned} $
7. Two adjacent angles are equal. Is it necessary that each of these angles will be a right angle? Justify your answer.
Show Answer
Solution
No, because if it will be a right angle only when they form a linear pair.
8. If one of the angles formed by two intersecting lines is a right angle, what can you say about the other three angles? Give reason for your answer.
Show Answer
Solution
If two intersecting line are formed right then by using linear pair axiom aniom, other three angles will be a right angle.
9. In Fig., which of the two lines are parallel and why?
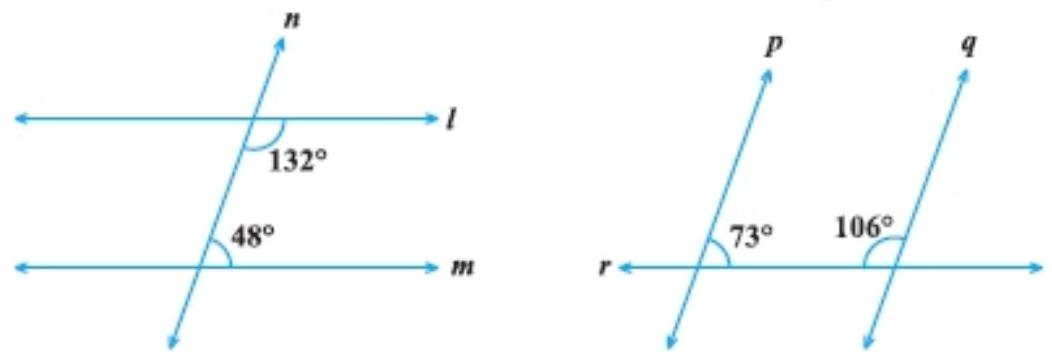
Show Answer
Solution
In the first figure, sum of two interior angle is: $132^{\circ}+48^{\circ}=180^{\circ}$ [Equal to $180^{\circ}$ ]
Hence, we know that, if sum of two interior angle are equal on the same side of $n$ is $180^{\circ}$, then they are the parallel lines.
In the second figure, sum of two interior angle is:
$73^{\circ}+106^{\circ}=179^{\circ} \neq 180^{\circ}$.
Hence, we know that, if sum of two interior angle are equal on the same side of $r$ is not equal to $180^{\circ}$, then they are not the parallel lines.
10. Two lines $l$ and $m$ are perpendicular to the same line $n$. Are $l$ and $m$ perpendicular to each other? Give reason for your answer.
Show Answer
Solution
If two lines $l$ and $m$ are perpendicular to the same line $n$, then each of the two corresponding angles formed by these lines $l$ and $m$ with the line $n$ are equal to $90^{\circ}$.
Hence the line $l$ and $m$ are not perpendicular but parallel.
Short Answer Questions
1. In Fig., $O D$ is the bisector of $\angle A O C, O E$ is the bisector of $\angle B O C$ and $O D$ $\perp O E$. Show that the points $A, O$ and $B$ are collinear.
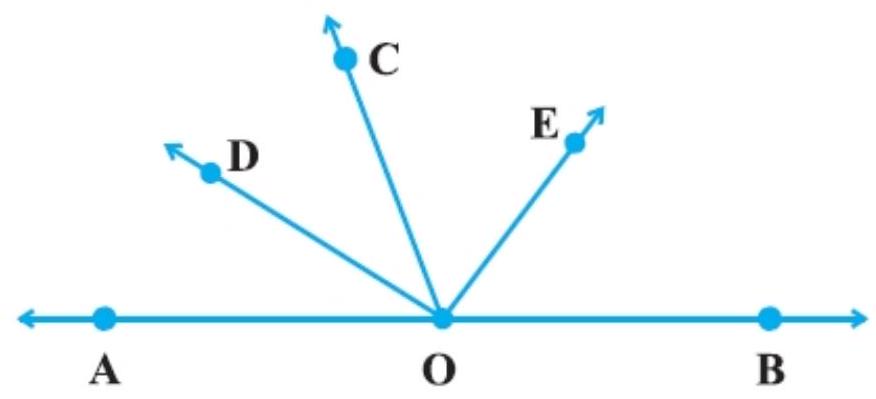
Show Answer
Solution
Given:
$OD$ is the bisector of $\angle AOC, OE$ is the bisector of $\angle BOC$ and $OD \perp OE$
To prove that point $A, O$ and $B$ are collinear that is $AOB$ are straight line.
$\angle A O C=2 \angle D O C$
$\angle C O B=2 \angle C O E$
Now, adding equations (I) and (II), get:
$\angle A O C+\angle C O B=2 \angle D O C+\angle C O E$
$\angle A O C+\angle C O B=2(\angle D O C+\angle C O E)$
$\angle A O C+\angle C O B=2 \angle D O C$
$\angle A O C+\angle C O B=2 \times 90^{\circ}$
$\angle A O C+\angle C O B=180^{\circ}$
$\angle A O C=180^{\circ}$
So, $\angle A O C+\angle C O B$ are forming linear pair or we can say that $AOB$ is a straight line.
Hence, point $A, O$ and $B$ are collinear.
2. In Fig., $\angle 1=60^{\circ}$ and $\angle 6=120^{\circ}$. Show that the lines $m$ and $n$ are parallel.
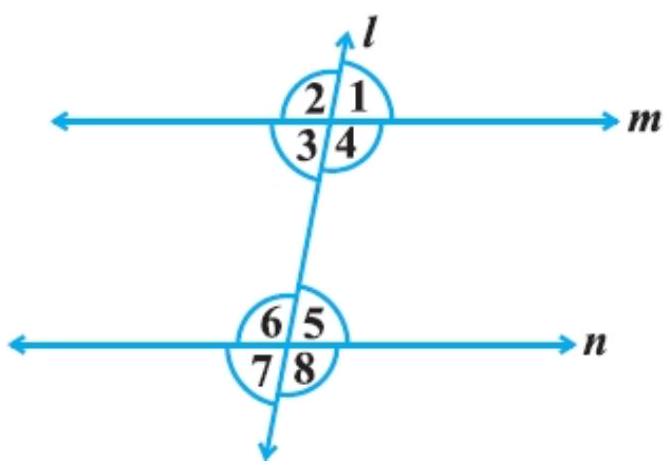
Show Answer
Solution
See the given figure,
$\angle 5+\angle 6=180^{\circ}$ (Linear pair angle)
$\angle 5+120^{\circ}=180^{\circ}$
$\angle 5=180^{\circ}-120^{\circ}$
$\angle 5=60^{\circ}$
Then, $\angle 1=\angle 5 \quad[Each=60^{\circ}]$
Since, these are corresponding angles.
Hence, the line $m$ and $n$ are parallel.
3. $AP$ and $BQ$ are the bisectors of the two alternate interior angles formed by the intersection of a transversal $t$ with parallel lines $l$ and $m$. Show that AP $||$ BQ.
Show Answer
Solution
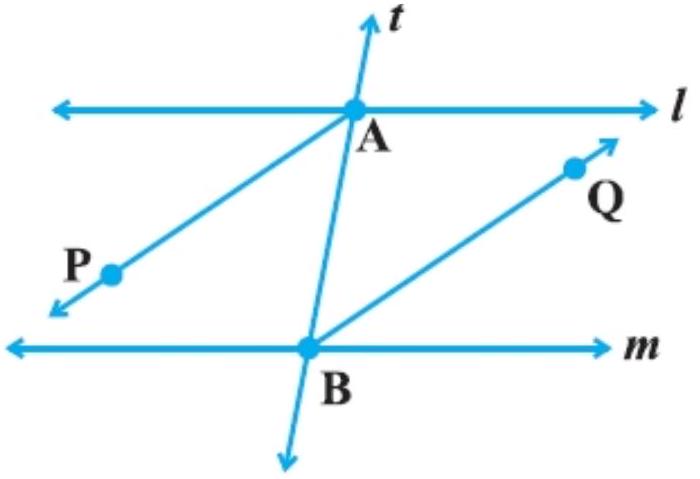
According to the question,
Line $l || m$ and $t$ is the transversal.
$\angle M A B=\angle S B A[$ Alt. $\angle s]$
$\dfrac{1}{2} \angle M A B=\dfrac{1}{2} \angle S B A$
$\angle P A B=\angle Q B A$
But, $\angle P A B$ and $\angle Q B A$ are alternate angles.
Hence, $AP || BQ$.
4. If in Fig., bisectors $A P$ and $B Q$ of the alternate interior angles are parallel, then show that $l || m$.
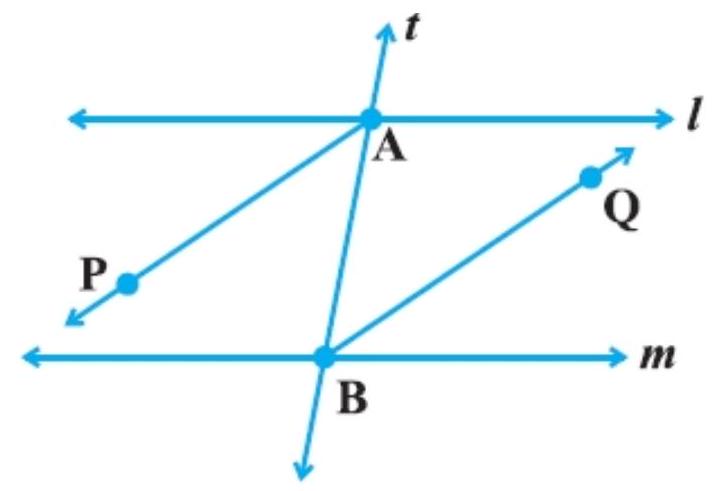
Show Answer
Solution
See the given figure, $AP || BQ, AP$ and $BQ$ are the bisectors of alternate interior angles $\angle C A B$ and $\angle A B F$.
To show that $l || m$.
Now, prove that $AP || BQ$ are $t$ is transversal, therefore:
$\angle P A B=\angle A B Q$ [Alternate interior angle]
$2 \angle P A B=2 \angle A B Q$ [Multiplying both sides by 2 in equation (I)]
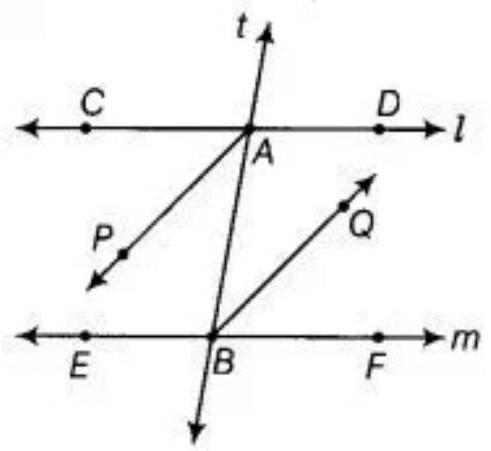
Since, alternate interior angle are equal.
So, if two alternate interior angle are equal then lines are parallel.
Hence, $l||m$.
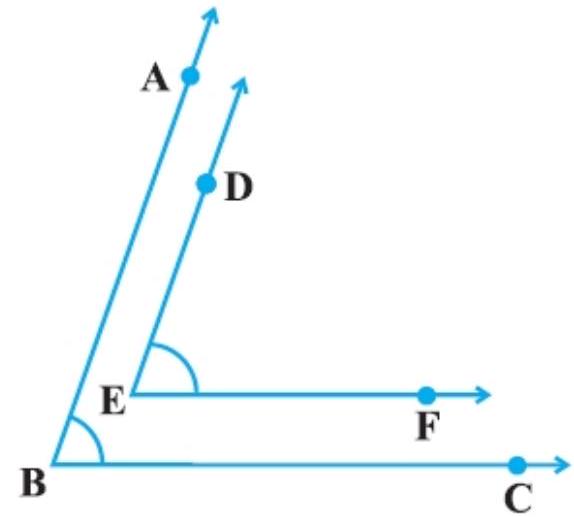
5. In Fig., BA $|| E D$ and $B C || E F$. Show that $\angle A B C=\angle D E F$.
[Hint: Produce DE to intersect BC at $P$ (say)].
Show Answer
Solution
According to the question:
Given:
Producing $DE$ to intersect $BC$ at $P$.
$EF || BC$ and $DP$ is the transversal,
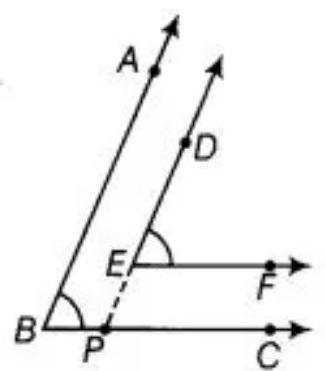
$\angle D E F=\angle D P C\quad$… (l) [Corresponding $\angle s$ ]
See the above figure, $AB || DP$ and $BC$ is the transversal,
$\angle D P C=\angle A B C\quad$… (II) [Corresponding $\angle s$ ]
Now, from equation (I) and (II), get:
$\angle A B C=\angle D E F$
Hence, proved.
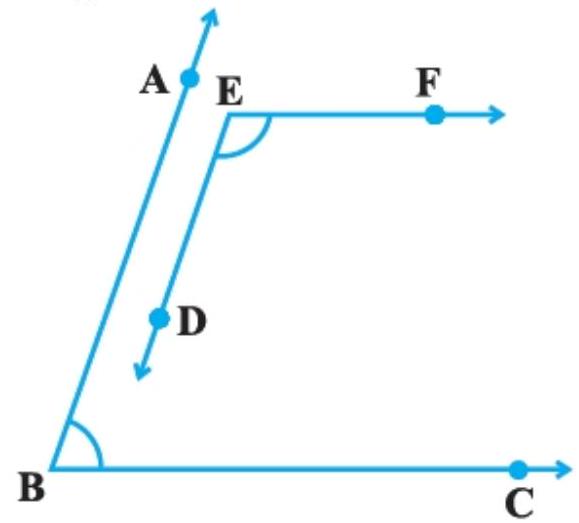
6. In Fig., BA $|| ED$ and $BC || EF$. Show that $\angle ABC+\angle DEF=180^{\circ}$.
Show Answer
Solution
See in the figure, $BA || ED$ and $BC || EF$.
Show that $\angle ABC+\angle DEF=180^{\circ}$.
Produce a ray PE opposite to ray EF.
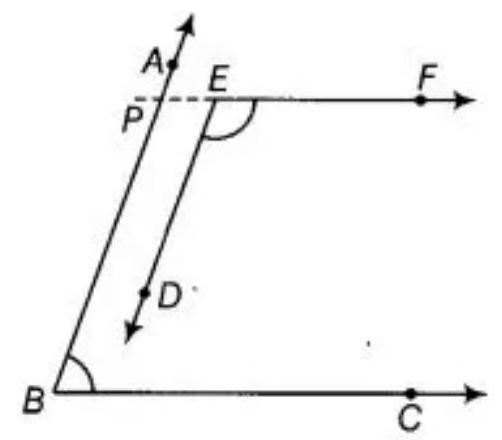
Prove: $BC|| EF$
Now, $\angle E P B+\angle P B C=180^{\circ} \quad$ [sum of co interior is $180^{\circ}$ ]
Now, $AB || ED$ and $PE$ is transversal line,
$\angle E P B=\angle D E F$ [Corresponding angles]
Now, from equation (I) and (II),
$\angle D E F+\angle P B C=180^{\circ}$
$\angle A B C+\angle D E F=180^{\circ}[$ Because $\angle P B C=\angle A B C]$
Hence, proved.
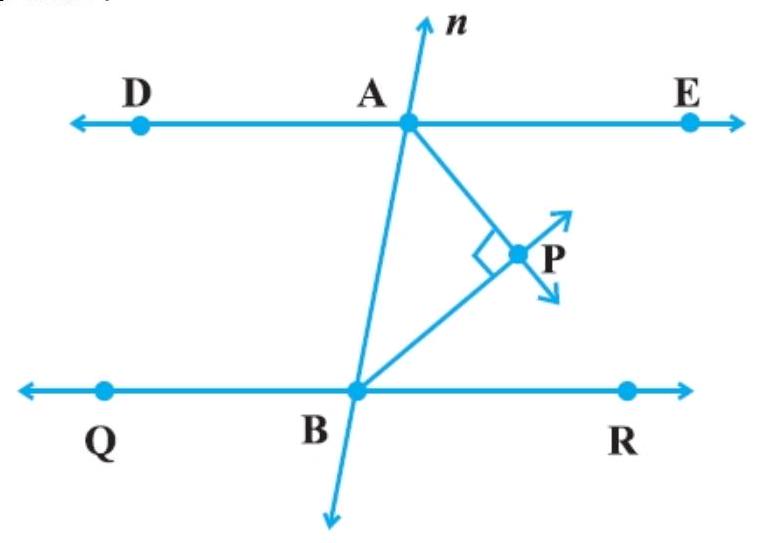
7. In Fig., DE $|| Q R$ and $A P$ and BP are bisectors of $\angle EAB$ and $\angle RBA$, respectively. Find $\angle A P B$.
Show Answer
Solution
See in the given figure, $DE || QR$ and the line $n$ is the transversal line. $\angle E A B+\angle R B A=180^{\circ} \ldots$ (I) [The interior angles on the same side of transversal are supplementary.]
Now, $\angle P A B+\angle P B A=90^{\circ}$
Then, from triangle APB, given: $\angle A P B=180^{\circ}-(\angle P A B+\angle P B A)$
So, $\angle A P B=180^{\circ}-90^{\circ}=90^{\circ}$
8. The angles of a triangle are in the ratio $2: 3: 4$. Find the angles of the triangle.
Show Answer
Solution
Given in the question, ratio of angles is: $2: 3: 4$.
Let the angles of the triangle be $2 x, 3 x$ and $4 x$.
So,
$2 x+3 x+4 x=180^{\circ}$ [sum of angles of triangle is $180^{\circ}$ ]
$9 x=180^{\circ}$
$x=\dfrac{180^{\circ}}{9}$
$x=20^{\circ}$
Therefore, $2 x=2 \times 20^{\circ}=40^{\circ}$
$3 x=2 \times 20^{\circ}=60^{\circ}$
And, $4 x=4 \times 20^{\circ}=80^{\circ}$
Hence, the angle of the triangles are $40^{\circ}, 60^{\circ}$ and $80^{\circ}$.
9. A triangle $A B C$ is right angled at $A$. $L$ is a point on $B C$ such that $A L \perp$ $B C$. Prove that $\angle B A L=\angle A C B$.
Show Answer
Solution
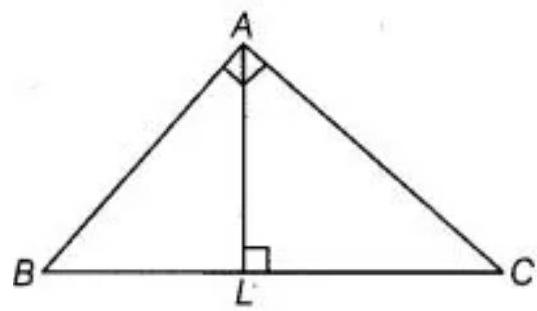
Given:
In triangle $ABC$,
$\angle A=90^{\circ}$ and $A L \perp B C$
To prove: $\angle B A L=\angle A C B$
Proof: Let $\angle A B C=x$
$\angle B A L=90^{\circ}-x$
As, $\angle A=x$
$\angle C A L=x$
$\angle A B C=\angle C A L$
$\angle A B C=\angle A C B$
Hence, proved.
10. Two lines are respectively perpendicular to two parallel lines. Show that they are parallel to each other.
Show Answer
Solution
According to the question:
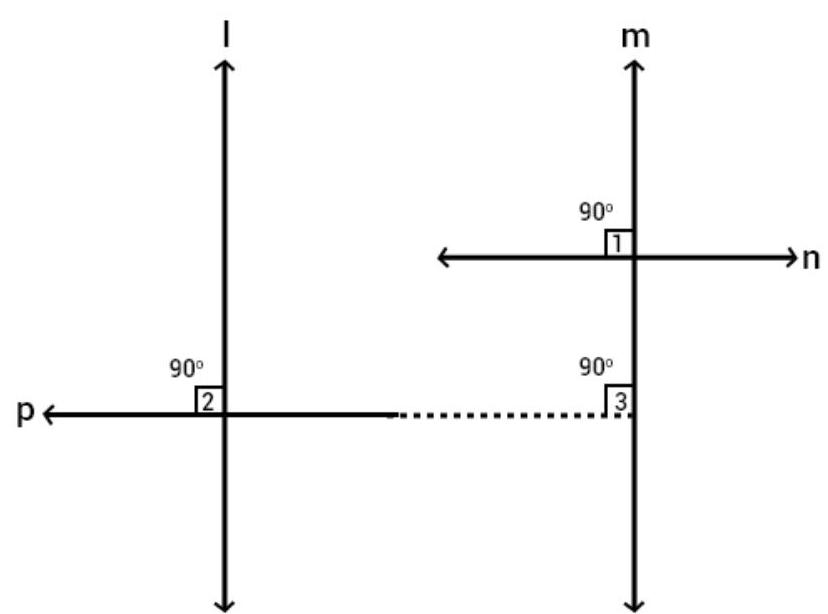
Two line $p$ and $n$ are respectively perpendicular to two parallel line $l$ and $m$, that is $P \perp l$ and $n \perp m$.
To prove that $p$ is parallel to $n$.
Given: $n \perp m$
So, $\angle 1=90^{\circ}$
Now, $P \perp l$
So, $\angle 2=90^{\circ}$
Since, 1 is parallel to $m$. So,
$\angle 2=\angle 3$
[Corresponding $\angle s$ ]
So,
$\angle 2=90^{\circ}$
From equation (I) and (II), get:
$\angle 1=\angle 3$
[each $90^{\circ}$ ]
But these are corresponding angles.
Hence, $p || n$.
Long Answer Questions
1. If two lines intersect, prove that the vertically opposite angles are equal.
Show Answer
Solution
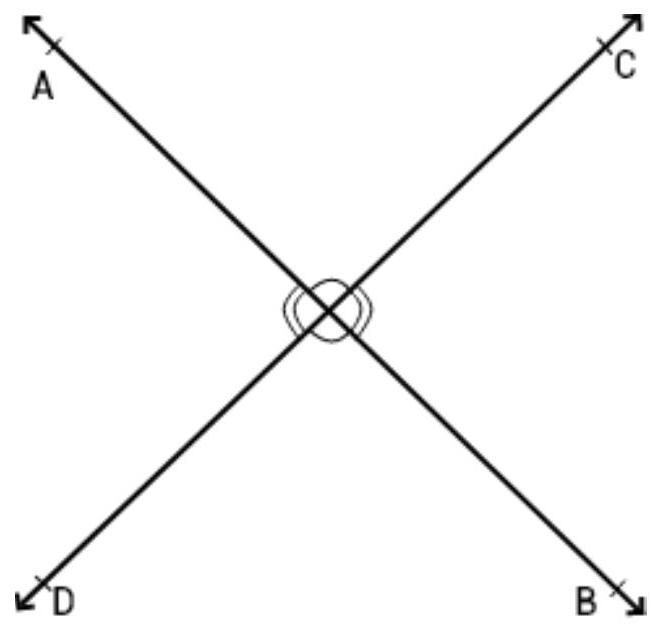
Two lines $AB$ and $CD$ intersect at point $O$.
To prove: (i) $\angle A O C=\angle B O D$
(ii) $\angle A O D=\angle B O C$
Proof: (i)
Ray on stands on line CD. So,
$\angle A O C+\angle A O D=180^{\circ} \ldots$ (I) [linear pair axiom]
Similarly, ray OD stands on line $AB$. So,
$\angle A O D+\angle B O D=180^{\circ}$
Now, from equation (I) and (II), get:
$\angle A O C+\angle A O D=\angle A O D+\angle B O D$
$ \angle A O C=\angle B O D $
Hence, proved.
(ii) Ray OD stands on line $AB$. $\angle A O D+\angle B O D=180^{\circ}$ … (III) [Linear pair axiom]
Similarly, ray $OB$ stands on line $CD$. So,
$\angle D O B+\angle B O C=180^{\circ}$
From equations (III) and (IV), get:
$\angle A O D+\angle B O D=\angle D O B+\angle B O C$
$ \angle A O D=\angle B O C $
Hence, proved.
2. Bisectors of interior $\angle B$ and exterior $\angle A C D$ of a $\triangle A B C$ intersect at the point T. Prove that
$\angle BTC=\dfrac{1}{2} \angle BAC$
Show Answer
Solution
Given: in triangle $ABC$, produce $BC$ to $D$ and the bisectors of $\angle A B C$ and $\angle A C D$ meet at point T.
To prove that $\angle B T C=\dfrac{1}{2} \angle B A C$
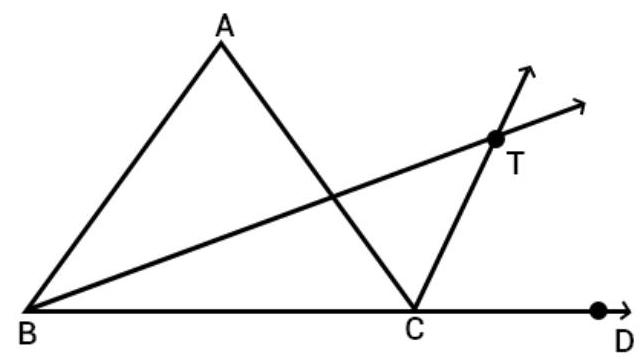
Proof: In triangle $ABC, \angle A C D$ is an exterior angle.
$\angle A C D=\angle A B C+\angle C A B$ [We know that exterior angle of a triangle is equal to the sum of two opposite angle]
$\dfrac{1}{2} \angle A C D=\dfrac{1}{2} \angle C A B+\dfrac{1}{2} \angle A B C$ [Dividing both sides by 2 in the above equation]
$\angle T C D=\dfrac{1}{2} \angle C A B+\dfrac{1}{2} \angle A B C$
[Since, CT is the bisector of
$\angle A C D$ that is $.\dfrac{1}{2} \angle A C D=\angle T C D]$
Now, in triangle BTC,
$\angle T C D=\angle B T C+\angle C B T$ [We know that exterior angle of the triangle is equal to the sum of two opposite angles]
$\angle T C D=\angle B T C+\dfrac{1}{2} \angle A B C$
…(II) [Since, BT is the bisector of triangle
$.ABC \angle C B T=\dfrac{1}{2} \angle A B C]$
Now, from equation (I) and (II), get:
$ \begin{aligned} \dfrac{1}{2} \angle C A B+\dfrac{1}{2} \angle A B C & =\angle B T C+\dfrac{1}{2} \angle A B C \\ \dfrac{1}{2} \angle C A B & =\angle B T C \\ \dfrac{1}{2} \angle B A C & =\angle B T C \end{aligned} $
Hence, proved.
3. A transversal intersects two parallel lines. Prove that the bisectors of any pair of corresponding angles so formed are parallel.
Show Answer
Solution
Given: Lines DE $|| QR$ and the line $DE$ intersected by transversal at $A$ and the line $QR$ intersected by transversal at $B$. Also, $BP$ and $AF$ are the bisector of angle $\angle A B R$ and $\angle C A E$ respectively.
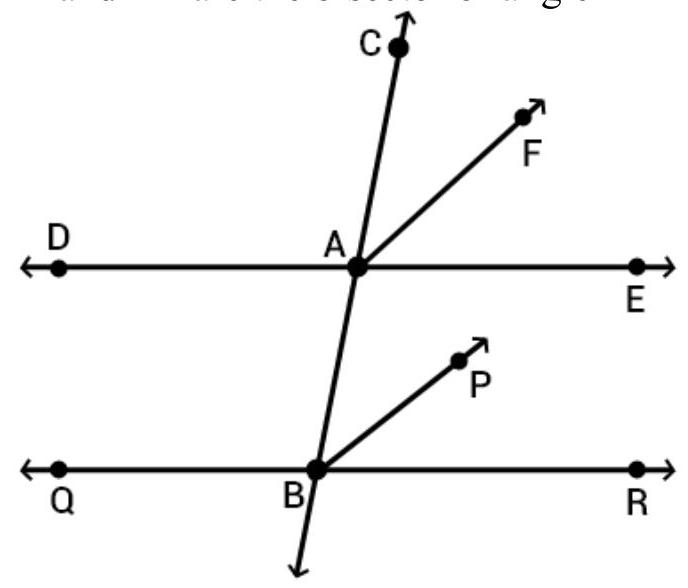
To prove: $BP || FA$
Proof: DE $|| QR$
$\angle C A E=\angle A B R$ [Corresponding angles]
$\dfrac{1}{2} \angle C A E=\dfrac{1}{2} \angle A B R$ [Dividing both side by 2 in the above equation]
$\angle C A F=\angle A B P$ [Since, bisector of angle $\angle A B R$ and $\angle C A E$ are BP and AF respectively]
Because these are the corresponding angles on transversal line $n$ and are equal.
Hence, BP $||$ FA.
4. Prove that through a given point, we can draw only one perpendicular to a given line.
[Hint: Use proof by contradiction].
Show Answer
Solution
Drawn a perpendicular line from the point $p$ as $PM \perp AB$. So, $\angle P M B=90^{\circ}$
Let if possible, drown another perpendicular line $PN \perp AB$. So, $\angle P M B=90^{\circ}$
Since, $\angle P M B=\angle P N B$ it will be possible when $PM$ and $PN$ coincide with each other.
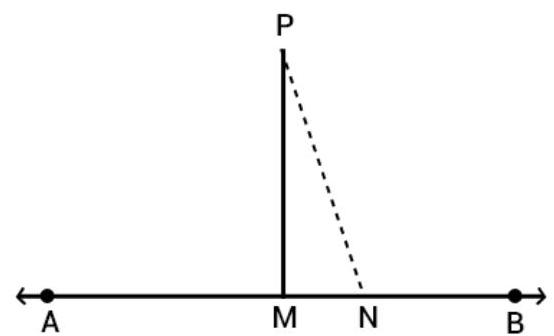
Therefore, at a given point we can draw only one perpendicular to a given line.
5. Prove that two lines that are respectively perpendicular to two intersecting lines intersect each other.
[Hint: Use proof by contradiction].
Show Answer
Solution
Given:
Let lines $l$ and $m$ are two intersecting lines. Again, let $n \perp p$ to the intersecting lines meet at point $D$.
To prove that two lines $n$ and $p$ intersecting at a point.
Proof:
Let consider that line $n$ and $p$ are intersecting each other it means lines $n$ and $p$ are parallel to each other.
$n || p$
Therefore, lines $n$ and $p$ are perpendicular to $m$ and $l$ respectively.
Now, by using equation (I), $n | p$, it means that $l$ and $m$. it is a contradiction.
Since, our assumption is wrong.
Hence, line $n$ and $p$ are intersect at a point.
6. Prove that a triangle must have at least two acute angles.
Show Answer
Solution
If triangle is an acute triangle then all the angle will be acute angle and sum of the all angle will be $180^{\circ}$.
If a triangle is a right angle triangle then one angle will be equal to $90^{\circ}$ and remaining two angle will be acute angles and sum of all the angles will be $180^{\circ}$.
Hence, a triangle must have at least two acute angles.
7. In Fig., $\angle Q>\angle R, PA$ is the bisector of $\angle QPR$ and $PM \perp QR$. Prove that $\angle APM=\dfrac{1}{2}(\angle Q-\angle R)$
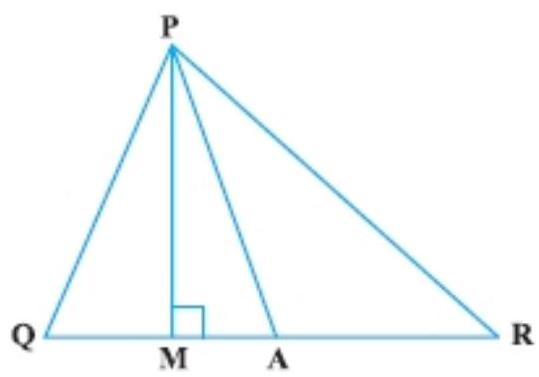
Show Answer
Solution
Given in triangle $PQR, \angle Q>\angle R$, $PA$ is the bisector of $\angle Q P R$ and $PM \perp QR$.
To prove that $\angle A P M=\dfrac{1}{2}(\angle Q-\angle R)$
Proof: PA is the bisector of $\angle Q P R$. So,
$\angle Q P A=\angle A P R$
In angle $PQM, \angle Q+\angle P M Q+\angle Q P M=180^{\circ}$
(I) [Angle sum property of a triangle]
$\angle Q+90^{\circ}+\angle Q P M=180^{\circ} \quad[\angle P M R=90^{\circ}]$
$\angle Q=90^{\circ}-\angle Q P M$
In triangle PMR, $\angle P M R+\angle R+\angle R P M=180^{\circ}$ [Angle sum property of a triangle]
$90^{\circ}+\angle R+\angle R P M=180^{\circ}[\angle P M R=90^{\circ}]$
$\angle R=180^{\circ}-90^{\circ}-\angle R P M$
$\angle R=180^{\circ}-90^{\circ}-\angle R P M$
$\angle R=90^{\circ}-\angle R P M$
Subtracting equation (III) from equation (II), get:
$$ \begin{align*} & \angle Q-\angle R=(90^{\circ}-\angle A P M)-(90^{\circ}-\angle R P M) \\ & \angle Q-\angle R=\angle R P M-\angle Q P M \\ & \angle Q-\angle R=(\angle R P A+\angle A P M)-(\angle Q P A-\angle A P M) \quad \ldots(IV) \\ & \angle Q-\angle R=\angle Q P A+\angle A P M-\angle Q P A+\angle A P M \text{ [As, } \angle R P A=\angle Q P A] \\ & \angle Q-\angle R=2 \angle A P M \\ & \angle A P M=\dfrac{1}{2}(\angle Q-\angle R) \end{align*} $$
Hence, proved.





