Solution

Let $\alpha=60^{\circ}, \beta=45^{\circ}$ and the angle inclined to OZ axis be $\gamma$

We know that

$\cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma=1$

$\Rightarrow \cos ^{2} 60^{\circ}+\cos ^{2} 45^{\circ}+\cos ^{2} \gamma=1$

$\Rightarrow \quad(\frac{1}{2})^{2}+(\frac{1}{\sqrt{2}})^{2}+\cos ^{2} \gamma=1 \quad \Rightarrow \quad \frac{1}{4}+\frac{1}{2}+\cos ^{2} \gamma=1$

$\Rightarrow \quad \frac{3}{4}+\cos ^{2} \gamma=1 \Rightarrow \cos ^{2} \gamma=1-\frac{3}{4}=\frac{1}{4}$

$\therefore \quad \cos \gamma= \pm \frac{1}{2} \Rightarrow \cos \gamma=\frac{1}{2}$

(Rejecting $\cos \gamma=-\frac{1}{2}$, since $\gamma<90^{\circ}$ )

$\therefore \quad \overrightarrow{{}OA}=|\overrightarrow{{}OA}|(\frac{1}{2} \hat{i}+\frac{1}{\sqrt{2}} \hat{j}+\frac{1}{2} \hat{k})=10(\frac{1}{2} \hat{i}+\frac{1}{\sqrt{2}} \hat{j}+\frac{1}{2} \hat{k})$

$=5 \hat{i}+5 \sqrt{2} \hat{j}+5 \hat{k}$

Hence, the position vector of $A$ is $(5 \hat{i}+5 \sqrt{2} \hat{j}+5 \hat{k})$.

Solution

We know that the equation of line is

$ \vec{r}=\vec{a}+\vec{b} \lambda $

Here, $\vec{a}=\hat{i}-2 \hat{j}+3 \hat{k}$ and $b \overrightarrow{{}3} \hat{i}-2 \hat{j}+6 \hat{k}$

$\therefore$ Equation of line is $\vec{r}=(\hat{i}-2 \hat{j}+3 \hat{k})+\lambda(3 \hat{i}-2 \hat{j}+6 \hat{k}) \Rightarrow$

$(x\hat{i} + y \hat{j}+ z \hat{k}) \neq (\hat{i}-2 \hat{j}+3 \hat{k})+\lambda(3 \hat{i}-2 \hat{j}+6 \hat{k})$

$\Rightarrow(x \hat{i}+y \hat{j}+z \hat{k})-(\hat{i}-2 \hat{j}+3 \hat{k})=\lambda(3 \hat{i}-2 \hat{j}+6 \hat{k})$

$\Rightarrow(x-1) \hat{i}+(y+2) \hat{j}+(z-3) \hat{k}=\lambda(3 \hat{i}-2 \hat{j}+6 \hat{k})$ Hence,

the required equation is

$(x-1) \hat{i}+(y+2) \hat{j}+(z-3) \hat{k}=\lambda(3 \hat{i}-2 \hat{j}+6 \hat{k})$

Solution

The given equations are

$ \begin{aligned} & \frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4} \text{ and } \frac{x-4}{5}=\frac{y-1}{2}=z \\ & \text{ Let } \quad \frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}=\lambda \\ & \therefore x=2 \lambda+1, y=3 \lambda+2 \text{ and } z=4 \lambda+3 \\ & \text{ and } \quad \frac{x-4}{5}=\frac{y-1}{2}=\frac{z}{1}=\mu \\ & \therefore x=5 \mu+4, y=2 \mu+1 \text{ and } z=\mu \end{aligned} $

If the two lines intersect each other at one point,

then $2 \lambda+1=5 \mu+4 \Rightarrow 2 \lambda-5 \mu=3\quad …$(i)

$3 \lambda-2 \mu=-1 3 \lambda+2=2 \mu+1 \Rightarrow 3 \lambda-2 \mu=-1 \quad …$(ii)

and $4 \lambda+3=\mu \quad \Rightarrow 4 \lambda-\mu=-3 \quad …$(iii)

Solving eqns. (i) and (ii) we get

$\begin{aligned} \Rightarrow 6 \lambda-15 \mu=9 \\ 6 \lambda-4 \mu=-2 \\ (-) \quad (+) \quad (+) \\ \hline \quad -11 \mu =\quad 11 \\ \therefore \quad \mu=-1 \end{aligned}$

Putting the value of $\mu$ in eq. (i) we get,

$\lambda-5(-1) =3$

$\Rightarrow \quad 2 \lambda+5 =3$

$\Rightarrow \quad 2 \lambda =-2 \quad \therefore \lambda=-1$

Now putting the value of $\lambda$ and $\mu$ in eq. (iii) then

$ \begin{aligned} 4(-1)-(-1) & =-3 \\ -4+1 & =-3 \\ -3 & =-3 \text{ (satisfied) } \end{aligned} $

$\therefore$ Coordinates of the point of intersection are

$ \begin{aligned} & x=5(-1)+4=-5+4=-1 \\ & y=2(-1)+1=-2+1=-1 \\ & z=-1 \end{aligned} $

Hence, the given lines intersect each other at $(-1,-1,-1)$.

Alternately: If two lines intersect each other at a point, then the shortest distance between them is equal to 0 .

For this we will use SD $=\frac{( \vec{a} _2- \vec{a} _1)( \vec{b} _1 \times \vec{b} _2)}{| \vec{b} _1 \times \vec{b} _2|}=0$.

Solution

Here,

$ \vec{b} _1=2 \hat{i}+\hat{j}+2 \hat{k} \text{ and } \vec{b} _2=6 \hat{i}+3 \hat{j}+2 \hat{k} $

$ \begin{aligned} \therefore \quad \cos \theta & =\frac{ \vec{b} _1 \cdot \vec{b} _2}{| \vec{b} _1| \vec{b} _2 \mid}=\frac{(2 \hat{i}+\hat{j}+2 \hat{k}) \cdot(6 \hat{i}+3 \hat{j}+2 \hat{k})}{\sqrt{(2)^{2}+(1)^{2}+(2)^{2}} \cdot \sqrt{(6)^{2}+(3)^{2}+(2)^{2}}} \\ & =\frac{12+3+4}{\sqrt{4+1+4} \cdot \sqrt{36+9+4}}=\frac{19}{\sqrt{9} \cdot \sqrt{49}}=\frac{19}{3 \cdot 7}=\frac{19}{21} \\ \therefore \quad \theta & =\cos ^{-1}(\frac{19}{21}) \end{aligned} $

Hence, the required angle is $\cos ^{-1}(\frac{19}{21})$.

Solution

Given points are $A(0,-1,-1)$ and $B(4,5,1)$

$ C(3,9,4) \text{ and } D(-4,4,4) $

Cartesian form of equation $AB$ is

$ \frac{x-0}{4-0}=\frac{y+1}{5+1}=\frac{z+1}{1+1} \Rightarrow \frac{x}{4}=\frac{y+1}{6}=\frac{z+1}{2} $

and its vector form is $\vec{r}=(-\hat{j}-\hat{k})+\lambda(4 \hat{i}+6 \hat{j}+2 \hat{k})$

Similarly, equation of $CD$ is

$ \frac{x-3}{-4-3}=\frac{y-9}{4-9}=\frac{z-4}{4-4} \Rightarrow \frac{x-3}{-7}=\frac{y-9}{-5}=\frac{z-4}{0} $

and its vector form is $\vec{r}=(3 \hat{i}+9 \hat{j}+4 \hat{k})+\mu(-7 \hat{i}-5 \hat{j})$

Now, here $ \vec{a} _1=-\hat{j}-\hat{k}, \vec{b} _1=4 \hat{i}+6 \hat{j}+2 \hat{k}$

$ \vec{a} _2=3 \hat{i}+9 \hat{j}+4 \hat{k}, \quad \vec{b} _2=-7 \hat{i}-5 \hat{j} $

Shortest distance between $AB$ and $CD$

$ \begin{aligned} \text{ S.D. } & =|\frac{( \vec{a} _2- \vec{a} _1) \cdot( \vec{b} _1 \times \vec{b} _2)}{| \vec{b} _1 \times \vec{b} _2|}| \\ \vec{a} _2- \vec{a} _1 & =(3 \hat{i}+9 \hat{j}+4 \hat{k})-(-\hat{j}-\hat{k})=3 \hat{i}+10 \hat{j}+5 \hat{k} . \\ \vec{b} _1 \times \vec{b} _2 & = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 4 & 6 & 2 \\ -7 & -5 & 0 \end{vmatrix} \\ & =\hat{i}(0+10)-\hat{j}(0+14)+\hat{k}(-20+42) \\ & =10 \hat{i}-14 \hat{j}+22 \hat{k} \end{aligned} $

$ \begin{aligned} | \vec{b} _1 \times \vec{b} _2| & =\sqrt{(10)^{2}+(-14)^{2}+(22)^{2}} \\ & =\sqrt{100+196+484}=\sqrt{780} \\ \therefore \quad \quad \text{ S.D } & =\frac{(3 \hat{i}+10 \hat{j}+5 \hat{k}) \cdot(10 \hat{i}-14 \hat{j}+22 \hat{k})}{\sqrt{780}} \\ & =\frac{30-140+110}{\sqrt{780}}=0 \end{aligned} $

Hence, the two lines intersect each other.

Solution

Given that: $\quad x=p y+q \Rightarrow y=\frac{x-q}{p}$

and $ z=r y+s \Rightarrow y=\frac{z-s}{r} $

$\therefore$ the equation becomes

$\frac{x-q}{p}=\frac{y}{1}=\frac{z-s}{r}$ in which d’ratios are $a_1=p, b_1=1, c_1=r$

Similarly

$ x=p^{\prime} y+q^{\prime} \Rightarrow y=\frac{x-q^{\prime}}{p^{\prime}} $

and $ z=r^{\prime} y+s^{\prime} \Rightarrow y=\frac{z-s^{\prime}}{r^{\prime}} $

$\therefore$ the equation becomes

$ \frac{x-q^{\prime}}{p^{\prime}}=\frac{y}{1}=\frac{z-s^{\prime}}{r^{\prime}} \text{ in which } a_2=p^{\prime}, b_2=1, c_2=r^{\prime} $

If the lines are perpendicular to each other, then

$ \begin{matrix} a_1 a_2+b_1 b_2+c_1 c_2=0 \\ p p^{\prime}+1.1+r r^{\prime}=0 \end{matrix} $

Hence, $p p^{\prime}+r r^{\prime}+1=0$ is the required condition.

Solution

Given that $A(2,3,4)$ and $B(4,5,8)$

Coordinates of mid-point $C$ are $(\frac{2+4}{2}, \frac{3+5}{2}, \frac{4+8}{2})=(3,4,6)$

Now direction ratios of the normal to the plane

$ \begin{aligned} & =\text{ direction ratios of } AB \\ & =4-2,5-3,8-4=(2,2,4) \end{aligned} $

Equation of the plane is

$a(x-x_1)+b(y-y_1)+c(z-z_1) =0 $

$\Rightarrow \quad 2(x-3)+2(y-4)+4(z-6) =0 $

$\Rightarrow \quad 2 x-6+2 y-8+4 z-24 =0$

$\Rightarrow \quad 2 x+2 y+4 z =38 \quad \Rightarrow \quad x+y+2 z=19$

Hence, the required equation of plane is $x+y+2 z=19 \quad$ or $\quad \vec{r}(\hat{i}+\hat{j}+2 \hat{k})=19$.

Solution

Since, the normal to the plane is equally inclined to the axes

$\therefore \cos \alpha=\cos \beta=\cos \gamma$

$\Rightarrow \cos ^{2} \alpha+\cos ^{2} \alpha+\cos ^{2} \alpha=1$

$\begin{aligned} \Rightarrow 3 \cos ^{2} \alpha =1 \Rightarrow \cos \alpha=\frac{1}{\sqrt{3}} \\ \Rightarrow \cos \alpha =\cos \beta=\cos \gamma=\frac{1}{\sqrt{3}}\end{aligned}$

So, the normal is

$ \overrightarrow{{}N}=\frac{1}{\sqrt{3}} \hat{i}+\frac{1}{\sqrt{3}} \hat{j}+\frac{1}{\sqrt{3}} \hat{k} $

$\therefore$ Equation of the plane is $\vec{r} \cdot \vec{N}=d$

$ \begin{aligned} & \Rightarrow \quad \vec{r} \cdot \frac{\vec{N}}{|\vec{N}|}=d \\ & \Rightarrow \quad \frac{\vec{r} \cdot(\frac{1}{\sqrt{3}} \hat{i}+\frac{1}{\sqrt{3}} \hat{j}+\frac{1}{\sqrt{3}} \hat{k})}{1}=3 \sqrt{3} \\ & \Rightarrow \quad \vec{r} \cdot(\frac{1}{\sqrt{3}} \hat{i}+\frac{1}{\sqrt{3}} \hat{j}+\frac{1}{\sqrt{3}} \hat{k})=3 \sqrt{3} \\ & \Rightarrow(x \hat{i}+y \hat{j}+z \hat{k}) \cdot \frac{1}{\sqrt{3}}(\hat{i}+\hat{j}+\hat{k})=3 \sqrt{3} \\ & \Rightarrow \quad x+y+z=3 \sqrt{3} \cdot \sqrt{3} \Rightarrow x+y+z=9 \end{aligned} $

Hence, the required equation of plane is $x+y+z=9$.

Solution

Direction ratios of the normal to the plane are

$(1+2,-3+1,3+3) \Rightarrow(3,-2,6)$

Equation of plane passing through one point $(x_1, y_1, z_1)$ is

$a(x-x_1)+b(y-y_1)+c(z-z_1) =0 $

$\Rightarrow \quad 3(x-1)-2(y+3)+6(z-3) =0 $

$\Rightarrow \quad 3 x-3-2 y-6+6 z-18 =0$

$\Rightarrow \quad 3 x-2 y+6 z-27 =0 \quad \Rightarrow 3 x-2 y+6 z=27$

Hence, the required equation is $3 x-2 y+6 z=27$.

Solution

Since, the equation of the plane passing through the points $(x_1, y_1, z_1),(x_2, y_2, z_2)$ and $(x_3, y_3, z_3)$ is

$ \begin{aligned} & \Rightarrow \begin{vmatrix} x-x_1 & y-y_1 & z-z_1 \\ x_2-x_1 & y_2-y_1 & z_2-z_1 \\ x_3-x_1 & y_3-y_1 & z_3-z_1 \end{vmatrix} =0 \\ & \Rightarrow \begin{vmatrix} x-2 & y-1 & z-0 \\ 3-2 & -2-1 & -2-0 \\ 3-2 & 1-1 & 7-0 \end{vmatrix} =0 \Rightarrow \begin{vmatrix} x-2 & y-1 & z \\ 1 & -3 & -2 \\ 1 & 0 & 7 \end{vmatrix} =0 \\ & \Rightarrow(x-2) \begin{vmatrix} -3 & -2 \\ 0 & 7 \end{vmatrix} -(y-1) \begin{vmatrix} 1 & -2 \\ 1 & 7 \end{vmatrix} +z \begin{vmatrix} 1 & -3 \\ 1 & 0 \end{vmatrix} =0 \\ & \Rightarrow \quad(x-2)(-21)-(y-1)(7+2)+z(3)=0 \\ & \Rightarrow \quad-21(x-2)-9(y-1)+3 z=0 \\ & \Rightarrow \quad-21 x+42-9 y+9+3 z=0 \\ & \Rightarrow \quad-21 x-9 y+3 z+51=0 \Rightarrow 7 x+3 y-z-17=0 \end{aligned} $

Hence, the required equation is $7 x+3 y-z-17=0$.

Solution

Any point on the given line is

$ \begin{aligned} \frac{x-3}{2} & =\frac{y-3}{1}=\frac{z}{1}=\lambda \\ \Rightarrow \quad x & =2 \lambda+3, y=\lambda+3 \\ \text{ and } \quad z & =\lambda \end{aligned} $

Let it be the coordinates of $P$

$\therefore$ Direction ratios of OP

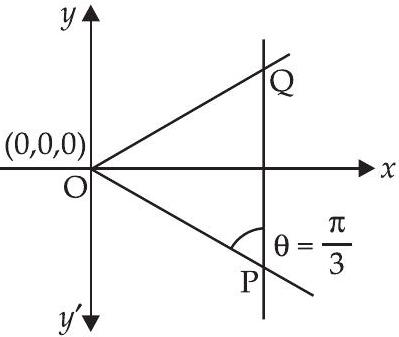
are

$(2 \lambda+3-0),(\lambda+3-0)$ and $(\lambda-0) \Rightarrow 2 \lambda+3, \lambda+3, \lambda$

But the direction ratios of the line PQ are 2, 1,1

$\begin{aligned}\cos \theta =\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\sqrt{a_1^{2}+b_1^{2}+c_1^{2}} \cdot \sqrt{a_2^{2}+b_2^{2}+c_2^{2}}}\end{aligned}$

$\begin{aligned}\cos \frac{\pi}{3} =\frac{2(2 \lambda+3)+1(\lambda+3)+1 . \lambda}{\sqrt{(2)^{2}+(1)^{2}+(1)^{2}} \cdot \sqrt{(2 \lambda+3)^{2}+(\lambda+3)^{2}+\lambda^{2}}}\end{aligned} $

$\begin{aligned}\Rightarrow \quad \frac{1}{2} =\frac{4 \lambda+6+\lambda+3+\lambda}{\sqrt{6} \cdot \sqrt{4 \lambda^{2}+9+12 \lambda+\lambda^{2}+9+6 \lambda+\lambda^{2}}}\end{aligned} $

$\begin{aligned}\Rightarrow \quad \frac{\sqrt{6}}{2} =\frac{6 \lambda+9}{\sqrt{6 \lambda^{2}+18 \lambda+18}}=\frac{6 \lambda+9}{\sqrt{6} \sqrt{\lambda^{2}+3 \lambda+3}}\end{aligned}$

$ \begin{aligned} & \Rightarrow \quad \frac{6}{2}=\frac{3(2 \lambda+3)}{\sqrt{\lambda^{2}+3 \lambda+3}} \Rightarrow 3=\frac{3(2 \lambda+3)}{\sqrt{\lambda^{2}+3 \lambda+3}} \\ & \Rightarrow \quad 1=\frac{2 \lambda+3}{\sqrt{\lambda^{2}+3 \lambda+3}} \Rightarrow \sqrt{\lambda^{2}+3 \lambda+3}=2 \lambda+3 \\ & \Rightarrow \quad \lambda^{2}+3 \lambda+3=4 \lambda^{2}+9+12 \lambda \\ & \Rightarrow \quad 3 \lambda^{2}+9 \lambda+6=0 \quad \Rightarrow \lambda^{2}+3 \lambda+2=0 \\ & \Rightarrow \quad(\lambda+1)(\lambda+2)=0 \\ & \therefore \quad \lambda=-1, \lambda=-2 \\ & \therefore \text{ Direction ratios are }[2(-1)+3,-1+3,-1] \text{ i.e., } 1,2,-1 \text{ when } \\ & \lambda=-1 \text{ and }[2(-2)+3,-2+3,-2] \text{ i.e., }-1,1,-2 \text{ when } \lambda=-2 . \end{aligned} $

Hence, the required equations are

$ \frac{x}{1}=\frac{y}{2}=\frac{z}{-1} \text{ and } \frac{x}{-1}=\frac{y}{1}=\frac{z}{-2} . $

Solution

The given equations are

$$ \begin{align*} l+m+n & =0 \tag{i}\\ l^{2}+m^{2}-n^{2} & =0 \tag{ii} \end{align*} $$

From equation $(i) n=-(l+m)$

Putting the value of $n$ in eq. (ii) we get

$ \begin{aligned} & l^{2}+m^{2}+[-(l+m)^{2}]=0 \\ & \Rightarrow \quad l^{2}+m^{2}-l^{2}-m^{2}-2 l m=0 \\ & \Rightarrow \quad-2 lm=0 \\ & \Rightarrow \quad l m=0 \Rightarrow(-m-n) m=0[\because l=-m-n] \\ & \Rightarrow \quad(m+n) m=0 \Rightarrow m=0 \text{ or } m=-n \\ & \Rightarrow \quad l=0 \text{ or } l=-n \end{aligned} $

$\therefore$ Direction cosines of the two lines are

$0,-n, n$ and $-n, 0, n \Rightarrow 0,-1,1$ and $-1,0,1$

$\begin{aligned}\therefore \quad \cos \theta =\frac{(0 \hat{i}-\hat{j}+\hat{k}) \cdot(-\hat{i}+0 \hat{j}+\hat{k})}{\sqrt{(-1)^{2}+(1)^{2}} \sqrt{(-1)^{2}+(1)^{2}}}=\frac{1}{\sqrt{2} \cdot \sqrt{2}}=\frac{1}{2}\end{aligned}$

$\therefore \quad \theta =\frac{\pi}{3}$

Hence, the required angle is $\frac{\pi}{3}$.

Solution

Given that $l, m, n$ and $l+\delta l, m+\delta m, n+\delta n$, are the direction cosines of a variable line in two positions

$$ \begin{equation*} \therefore \quad l^{2}+m^{2}+n^{2}=1 \tag{i} \end{equation*} $$

$$ \begin{align*} & \text{ and }(l+\delta l)^{2}+(m+\delta m)^{2}+(n+\delta n)^{2}=1 \tag{ii}\\ & \Rightarrow l^{2}+\delta l^{2}+2 l . \delta l+m^{2}+\delta m^{2}+2 m . \delta m+n^{2}+\delta n^{2}+2 n . \delta n=1 \\ & \Rightarrow(l^{2}+m^{2}+n^{2})+(\delta l^{2}+\delta m^{2}+\delta n^{2})+2(l . \delta l+m . \delta m+n . \delta n)=1 \\ & \Rightarrow 1+(\delta l^{2}+\delta m^{2}+\delta n^{2})+2(l . \delta l+m . \delta m+n \cdot \delta n)=1 \\ & \Rightarrow l . \delta l+m . \delta m+n . \delta n=-\frac{1}{2}(\delta l^{2}+\delta m^{2}+\delta n^{2}) \end{align*} $$

Let $\vec{a}$ and $\vec{b}$ be the unit vectors along a line with d’cosines $l, m$, $n$ and $(l+\delta l),(m+\delta m),(n+\delta n)$.

$\therefore \vec{a}=l \hat{i}+m \hat{j}+n \hat{k}$ and $\vec{b}=(l+\delta l) \hat{i}+(m+\delta m) \hat{j}+(n+\delta n) \hat{k}$

$\cos \delta \theta=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}$

$\cos \delta \theta=\frac{(l \hat{i}+m \hat{j}+n \hat{k}) \cdot[(l+\delta l) \hat{i}+(m+\delta m) \hat{j}+(n+\delta n) \hat{k}]}{1.1}$ $\qquad [\because|\vec{a}|=|\vec{b}|=1]$

$\Rightarrow \quad \cos \delta \theta=l(l+\delta l)+m(m+\delta m)+n(n+\delta n)$

$\Rightarrow \quad \cos \delta \theta=l^{2}+l . \delta l+m^{2}+m . \delta m+n^{2}+n . \delta n$

$\Rightarrow \quad \cos \delta \theta=(l^{2}+m^{2}+n^{2})+(l . \delta l+m . \delta m+n . \delta n)$

$\Rightarrow \quad \cos \delta \theta=1-\frac{1}{2}(\delta l^{2}+\delta m^{2}+\delta n^{2})$

$\Rightarrow 1-\cos \delta \theta=\frac{1}{2}(\delta l^{2}+\delta m^{2}+\delta n^{2})$

$\Rightarrow 2 \sin ^{2} \frac{\delta \theta}{2}=\frac{1}{2}(\delta l^{2}+\delta m^{2}+\delta n^{2})$

$\Rightarrow 4 \sin ^{2} \frac{\delta \theta}{2}=\delta l^{2}+\delta m^{2}+\delta n^{2}$

$\Rightarrow 4(\frac{\delta \theta}{2})^{2}=\delta l^{2}+\delta m^{2}+\delta n^{2}$

$ \begin{bmatrix} \because \quad \frac{\delta \theta}{2} \text{ is very small so, } \\ \sin \frac{\delta \theta}{2}=\frac{\delta \theta}{2} \end{bmatrix} $

$\Rightarrow \quad(\delta \theta)^{2}=\delta l^{2}+\delta m^{2}+\delta n^{2}$ Hence proved.

Solution

We have $A(a, b, c)$ and $O(0,0,0)$

$\therefore$ direction ratios of $OA=a-0, b-0, c-0$

$ =a, b, c $

$\therefore$ direction cosines of line $OA$

$ =\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}, \frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}} $

Now direction ratios of the normal to the plane are $(a, b, c)$.

$\therefore$ Equation of the plane passing through the point $A(a, b, c)$ is

$ a(x-a)+b(y-b)+c(z-c)=0 $

$ \begin{aligned} \Rightarrow a x-a^{2}+b y-b^{2}+c z-c^{2} =0 \\ \Rightarrow a x+b y+c z =a^{2}+b^{2}+c^{2} \end{aligned} $

Hence, the required equation is $a x+b y+c z=a^{2}+b^{2}+c^{2}$.

Solution

Let OX, OY, OZ and $o x, o y, o z$ be two rectangular systems

$\therefore$ Equations of two planes are

$$ \begin{equation*} \frac{X}{a}+\frac{Y}{b}+\frac{Z}{c}=1 \ldots(i) \quad \text{ and } \quad \frac{x}{a^{\prime}}+\frac{y}{b^{\prime}}+\frac{z}{c^{\prime}}=1 \tag{ii} \end{equation*} $$

Length of perpendicular from origin to plane $(i)$ is

$ =|\frac{\frac{0}{a}+\frac{0}{b}+\frac{0}{c}-1}{\sqrt{\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}}}|=\frac{1}{\sqrt{\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}}} $

Length of perpendicular from origin to plane (ii)

$ =|\frac{\frac{0}{a^{\prime}}+\frac{0}{b^{\prime}}+\frac{0}{c^{\prime}}-1}{\sqrt{\frac{1}{a^{\prime 2}}+\frac{1}{b^{\prime 2}}+\frac{1}{c^{\prime 2}}}}|=\frac{1}{\sqrt{\frac{1}{a^{\prime 2}}+\frac{1}{b^{\prime 2}}+\frac{1}{c^{\prime 2}}}} $

As per the condition of the question

$ \frac{1}{\sqrt{\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}}}=\frac{1}{\sqrt{\frac{1}{a^{\prime 2}}+\frac{1}{b^{\prime 2}}+\frac{1}{c^{\prime 2}}}} $

Hence, $\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}=\frac{1}{a^{\prime 2}}+\frac{1}{b^{\prime 2}}+\frac{1}{c^{\prime 2}}$

Solution

Given that: $\quad \frac{4-x}{2}=\frac{y}{6}=\frac{1-z}{3}$ is the equation of line

$ \Rightarrow \quad \frac{x-4}{-2}=\frac{y}{6}=\frac{z-1}{-3}=\lambda $

$\therefore$ Coordinates of any point $Q$ on the line are $x=-2 \lambda+4, y=6 \lambda$ and $z=-3 \lambda+1$ and the given point is $P(2,3,-8)$

Direction ratios of PQ are $-2 \lambda+4-2,6 \lambda-3,-3 \lambda+1+8$

i.e., $-2 \lambda+2,6 \lambda-3,-3 \lambda+9$

and the D’ratios of the given line are $-2,6,-3$.

If $PQ \perp$ line

then $-2(-2 \lambda+2)+6(6 \lambda-3)-3(-3 \lambda+9)=0$

$\Rightarrow \quad 4 \lambda-4+36 \lambda-18+9 \lambda-27=0$

$\Rightarrow \quad 49 \lambda-49=0 \Rightarrow \lambda=1$

$\therefore$ The foot of the perpendicular is $-2(1)+4,6(1),-3(1)+1$

i.e., $2,6,-2$

$ \text{ Now, distance } \begin{aligned} P Q & =\sqrt{(2-2)^{2}+(3-6)^{2}+(-8+2)^{2}} \\ & =\sqrt{9+36}=\sqrt{45}=3 \sqrt{5} \end{aligned} $

Hence, the required coordinates of the foot of perpendicular are $2,6,-2$ and the required distance is $3 \sqrt{5}$ units.

Solution

The given equation of line is

$ \frac{x+5}{1}=\frac{y+3}{4}=\frac{z-6}{-9}=\lambda \text{ and any point } P(2,4,-1) $

Let $Q$ be any point on the given line

$\therefore$ Coordinates of $Q$ are $x=\lambda-5, y=4 \lambda-3, z=-9 \lambda+6$

D’ratios of PQ are $\lambda-5-2,4 \lambda-3-4,-9 \lambda+6+1$

i.e., $\lambda-7,4 \lambda-7,-9 \lambda+7$

and the d’ratios of the line are $1,4,-9$

If $PQ \perp$ line then

$ \begin{aligned} 1(\lambda-7)+4(4 \lambda-7)-9(-9 \lambda+7) & =0 \\ \lambda-7+16 \lambda-28+81 \lambda-63 & =0 \\ \Rightarrow \quad 98 \lambda-98 & =0 \quad \therefore \quad \lambda=1 \end{aligned} $

So, the coordinates of $Q$ are $1-5,4 \times 1-3,-9 \times 1+6$ i.e., $-4,1,-3$

$ \begin{aligned} \therefore \quad PQ & =\sqrt{(-4-2)^{2}+(1-4)^{2}+(-3+1)^{2}} \\ & =\sqrt{(-6)^{2}+(-3)^{2}+(-2)^{2}}=\sqrt{36+9+4}=\sqrt{49}=7 \end{aligned} $

Hence, the required distance is 7 units.

Solution

Given plane is $2 x-2 y+4 z+5=0$ and given point is $(1, \frac{3}{2}, 2)$

D’ratios of the normal to the plane are 2, - 2, 4

So, the equation of the line passing through $(1, \frac{3}{2}, 2)$ and whose d’ratios are equal to the d’ratios of the normal to the plane i.e., $2,-2,4$ is $\frac{x-1}{2}=\frac{y-\frac{3}{2}}{-2}=\frac{z-2}{4}=\lambda$

$\therefore$ Any point in the plane is $2 \lambda+1,-2 \lambda+\frac{3}{2}, 4 \lambda+2$

Since, the point lies in the plane, then

$2(2 \lambda+1)-2(-2 \lambda+\frac{3}{2})+4(4 \lambda+2)+5=0$

$\Rightarrow 4 \lambda+2+4 \lambda-3+16 \lambda+8+5=0$

$\Rightarrow 24 \lambda+12=0 \quad \therefore \lambda=-\frac{1}{2}$

So, the coordinates of the point in the plane are

$ 2(-\frac{1}{2})+1,-2(-\frac{1}{2})+\frac{3}{2}, 4(-\frac{1}{2})+2 \text{ i.e., } 0, \frac{5}{2}, 0 $

Hence, the foot of the perpendicular is $(0, \frac{5}{2}, 0)$ and the

$ \begin{aligned} \text{required length} \quad & =\sqrt{(1-0)^{2}+(\frac{3}{2}-\frac{5}{2})^{2}+(2-0)^{2}} \\ & =\sqrt{1+1+4}=\sqrt{6} \text{ units } \end{aligned} $

Solution

Given point is $(3,0,1)$ and the equation of planes are

and $\quad \begin{aligned} x+2 y & =0 \\ 3 y-z & =0\end{aligned}$

Equation of any line $l$ passing through $(3,0,1)$ is

$l: \frac{x-3}{a}=\frac{y-0}{b}=\frac{z-1}{c}$

Direction ratios of the normal to plane (i) and plane (ii) are

$(1,2,0)$ and $(0,3,-1)$

Since the line is parallel to both the planes.

$ \begin{matrix} \therefore & 1 \cdot a+2 \cdot b+0 . c=0 \Rightarrow a+2 b+0 c=0 \\ \text{ and } & 0 \cdot a+3 \cdot b-1 . c=0 \Rightarrow 0 \cdot a+3 b-c=0 \end{matrix} $

So

$ \frac{a}{-2-0}=\frac{-b}{-1-0}=\frac{c}{3-0}=\lambda $

$\therefore a=-2 \lambda, b=\lambda, c=3 \lambda$

So, the equation of line is

$ \frac{x-3}{-2 \lambda}=\frac{y}{\lambda}=\frac{z-1}{3 \lambda} $

Hence, the required equation is

or in vector form is

$ \frac{x-3}{-2}=\frac{y}{1}=\frac{z-1}{3} $

$ (x-3) \hat{i}+y \hat{j}+(z-1) \hat{k}=\lambda(-2 \hat{i}+\hat{j}+3 \hat{k}) $

Solution

Equation of the plane passing through two points $(x_1, y_1, z_1)$ and $(x_2, y_2, z_2)$ with its normal’s d’ratios is

$$ \begin{equation*} a(x-x_1)+b(y-y_1)+c(z-z_1)=0 \tag{i} \end{equation*} $$

If the plane is passing through the given points $(2,1,-1)$ and $(-1,3,4)$ then

$$ \begin{align*} & & a(x_2-x_1)+b(y_2-y_1)+c(z_2-z_1) & =0 \\ \Rightarrow & & a(-1-2)+b(3-1)+c(4+1) & =0 \\ \Rightarrow & & -3 a+2 b+5 c & =0 \tag{ii} \end{align*} $$

Since the required plane is perpendicular to the given plane $x-2 y+4 z=10$, then

$$ \begin{equation*} 1 . a-2 . b+4 . c=10 \tag{iii} \end{equation*} $$

Solving (ii) and (iii) we get,

$ \frac{a}{8+10}=\frac{-b}{-12-5}=\frac{c}{6-2}=\lambda $

$a=18 \lambda, b=17 \lambda, c=4 \lambda$

Hence, the required plane is

$ \begin{matrix} 18 \lambda(x-2)+17 \lambda(y-1)+4 \lambda(z+1) =0 \\ \Rightarrow 18 x-36+17 y-17+4 z+4 =0 \\ \Rightarrow 18 x+17 y+4 z-49 =0 \end{matrix} $

Solution

Given equations of lines are

$$ \begin{align*} \vec{r} & =(8+3 \lambda) \hat{i}-(9+16 \lambda) \hat{j}+(10+7 \lambda) \hat{k} \tag{i}\\ \text{ and } \quad \vec{r} & =15 \hat{i}+29 \hat{j}+5 \hat{k}+\mu(3 \hat{i}+8 \hat{j}-5 \hat{k}) \tag{ii} \end{align*} $$

Equation (i) can be re-written as

$$ \begin{equation*} \vec{r}=8 \hat{i}-9 \hat{j}+10 \hat{k}+\lambda(3 \hat{i}-16 \hat{j}+7 \hat{k}) \tag{iii} \end{equation*} $$

Here, $\quad \vec{a} _1=8 \hat{i}-9 \hat{j}+10 \hat{k}$ and $ \vec{a} _2=15 \hat{i}+29 \hat{j}+5 \hat{k}$

$ \begin{aligned} \vec{b} _1 & =3 \hat{i}-16 \hat{j}+7 \hat{k} \text{ and } \vec{b} _2=3 \hat{i}+8 \hat{j}-5 \hat{k} \\ \vec{a} _2- \vec{a} _1 & =7 \hat{i}+38 \hat{j}-5 \hat{k} \\ \vec{b} _1 \times \vec{b} _2 & = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & -16 & 7 \\ 3 & 8 & -5 \end{vmatrix} \end{aligned} $

$ \begin{aligned} & =\hat{i}(80-56)-\hat{j}(-15-21)+\hat{k}(24+48) \\ & =24 \hat{i}+36 \hat{j}+72 \hat{k} \end{aligned} $

$\therefore$ Shortest distance, SD $\begin{aligned}=|\frac{( \vec{a} _2- \vec{a} _1) \cdot( \vec{b} _1 \times \vec{b} _2)}{| \vec{b} _1 \times \vec{b} _2|}|\end{aligned}$

$ \begin{aligned} & =|\frac{(7 \hat{i}+38 \hat{j}-5 \hat{k}) \cdot(24 \hat{i}+36 \hat{j}+72 \hat{k})}{\sqrt{(24)^{2}+(36)^{2}+(72)^{2}}}| \\ & =|\frac{168+1368-360}{\sqrt{576+1296+5184}}|=|\frac{168+1008}{\sqrt{7056}}|=\frac{1176}{84}=14 \text{ units } \end{aligned} $

Hence, the required distance is 14 units.

Solution

The given planes are

$P_1: \quad 5 x+3 y+6 z+8=0$

$P_2: \quad x+2 y+3 z-4=0$

$P_3: \quad 2 x+y-z+5=0$

Equation of the plane passing through the line of intersection of $P_2$ and $P_3$ is

$ (x+2 y+3 z-4)+\lambda(2 x+y-z+5)=0 $

$$ \begin{equation*} \Rightarrow \quad(1+2 \lambda) x+(2+\lambda) y+(3-\lambda) z-4+5 \lambda=0 \tag{i} \end{equation*} $$

Plane (i) is perpendicular to $P_1$, then

$5(1+2 \lambda)+3(2+\lambda)+6(3-\lambda) =0 $

$\Rightarrow \quad 5 5+10 \lambda+6+3 \lambda+18-6 \lambda =0$

$\Rightarrow \quad 7 \lambda+29 =0 $

$\therefore \quad \lambda =\frac{-29}{7}$

Putting the value of $\lambda$ in eq. (i), we get

$ \begin{aligned} & {[1+2(\frac{-29}{7})] x+[2-\frac{29}{7}] y+[3+\frac{29}{7}] z-4+5(\frac{-29}{7})=0} \\ & \Rightarrow \frac{-15}{7} x-\frac{15}{7} y+\frac{50}{7} z-4-\frac{145}{7}=0 \\ & \Rightarrow-15 x-15 y+50 z-28-145=0 \\ & \Rightarrow-15 x-15 y+50 z-173=0 \Rightarrow 51 x+15 y-50 z+173=0 \end{aligned} $

Solution

Given planes are:

$$ \begin{align*} a x+b y & =0 \tag{i}\\ z & =0 \tag{ii} \end{align*} $$

Equation of any plane passing through the line of intersection of plane (i) and (ii) is

$$ \begin{equation*} (a x+b y)+k z=0 \Rightarrow a x+b y+k z=0 \tag{iii} \end{equation*} $$

Dividing both sides by $\sqrt{a^{2}+b^{2}+k^{2}}$, we get

$\begin{aligned}\frac{a}{\sqrt{a^{2}+b^{2}+k^{2}}} x+\frac{b}{\sqrt{a^{2}+b^{2}+k^{2}}} y+\frac{k}{\sqrt{a^{2}+b^{2}+k^{2}}} z=0\end{aligned}$

$\therefore$ Direction cosines of the normal to the plane are

$\begin{aligned}\frac{a}{\sqrt{a^{2}+b^{2}+k^{2}}}, \frac{b}{\sqrt{a^{2}+b^{2}+k^{2}}}, \frac{k}{\sqrt{a^{2}+b^{2}+k^{2}}}\end{aligned}$

and the direction cosines of the plane ( $i$ ) are

$\begin{aligned}\frac{a}{\sqrt{a^{2}+b^{2}}}, \frac{b}{\sqrt{a^{2}+b^{2}}}, 0\end{aligned}$

Since, $\alpha$ is the angle between the planes (i) and (iii), we get

$ \begin{aligned} & \cos \alpha=\frac{a \cdot a+b \cdot b+k \cdot 0}{\sqrt{a^{2}+b^{2}+k^{2}} \cdot \sqrt{a^{2}+b^{2}}} \\ & \Rightarrow \quad \cos \alpha=\frac{a^{2}+b^{2}}{\sqrt{a^{2}+b^{2}+k^{2}} \cdot \sqrt{a^{2}+b^{2}}} \\ & \Rightarrow \quad \cos \alpha=\frac{\sqrt{a^{2}+b^{2}}}{\sqrt{a^{2}+b^{2}+k^{2}}} \Rightarrow \cos ^{2} \alpha=\frac{a^{2}+b^{2}}{a^{2}+b^{2}+k^{2}} \\ & \Rightarrow(a^{2}+b^{2}+k^{2}) \cos ^{2} \alpha=a^{2}+b^{2} \\ & \Rightarrow a^{2} \cos ^{2} \alpha+b^{2} \cos ^{2} \alpha+k^{2} \cos ^{2} \alpha=a^{2}+b^{2} \\ & \Rightarrow \quad k^{2} \cos ^{2} \alpha=a^{2}-a^{2} \cos ^{2} \alpha+b^{2}-b^{2} \cos ^{2} \alpha \\ & \Rightarrow \quad k^{2} \cos ^{2} \alpha=\alpha^{2}(1-\cos ^{2} \alpha)+b^{2}(1-\cos ^{2} \alpha) \\ & \Rightarrow \quad k^{2} \cos ^{2} \alpha=a^{2} \sin ^{2} \alpha+b^{2} \sin ^{2} \alpha \\ & \Rightarrow \quad k^{2} \cos ^{2} \alpha=(a^{2}+b^{2}) \sin ^{2} \alpha \\ & \Rightarrow \quad k^{2}=(a^{2}+b^{2}) \frac{\sin ^{2} \alpha}{\cos ^{2} \alpha} \Rightarrow k= \pm \sqrt{a^{2}+b^{2}} \cdot \tan \alpha \end{aligned} $

Putting the value of $k$ in eq. (iii) we get

$a x+b y \pm(\sqrt{a^{2}+b^{2}} \cdot \tan \alpha) z=0$ which is the required equation of plane.

Hence proved.

Solution

Given planes are;

and $\begin{aligned} \quad \vec{r} \cdot(\hat{i}+3 \hat{j})-6=0 \quad & \Rightarrow \quad x+3 y-6=0 \\ \quad \vec{r} \cdot(3 \hat{i}-\hat{j}-4 \hat{k})=0 & \Rightarrow \quad 3 x-y-4 z=0\end{aligned}$

Equation of the plane passing through the line of intersection of plane (i) and (ii) is

$$ \begin{matrix} (x+3 y-6)+k(3 x-y-4 z)=0 \tag{iii}\\ (1+3 k) x+(3-k) y-4 k z-6=0 \end{matrix} $$

Perpendicular distance from origin

$\begin{aligned}=|\frac{-6}{\sqrt{(1+3 k)^{2}+(3-k)^{2}+(-4 k)^{2}}}|=1\end{aligned}$

$\begin{aligned}\Rightarrow \frac{36}{1+9 k^{2}+6 k+9+k^{2}-6 k+16 k^{2}}=1\end{aligned}$ [Squaring both sides]

$\begin{aligned}\Rightarrow \quad \frac{36}{26 k^{2}+10}=1 \Rightarrow 26 k^{2}+10=36\end{aligned}$

$\Rightarrow \quad 26 k^{2}=26 \quad \Rightarrow \quad k^{2}=1 \quad \therefore k= \pm 1$

Putting the value of $k$ in eq. (iii) we get,

$ (x+3 y-6) \pm(3 x-y-4 z)=0 $

$\Rightarrow x+3 y-6+3 x-y-4 z=0$ and $x+3 y-6-3 x+y+4 z=0$

$\Rightarrow 4 x+2 y-4 z-6=0$ and $-2 x+4 y+4 z-6=0$

Hence, the required equations are:

$4 x+2 y-4 z-6=0$ and $-2 x+4 y+4 z-6=0$.

Solution

Given points are $P(\hat{i}-\hat{j}+3 \hat{k})$ and $Q(3 \hat{i}+3 \hat{j}+3 \hat{k})$ and the plane $\vec{r} .(5 \hat{i}+2 \hat{j}-7 \hat{k})+9=0$

Perpendicular distance of $P(\hat{i}-\hat{j}+3 \hat{k})$ from the plane

$ \begin{aligned} \vec{r} .(5 \hat{i}+2 \hat{j}-7 \hat{k})+9 & =|\frac{(\hat{i}-\hat{j}+3 \hat{k}) \cdot(5 \hat{i}+2 \hat{j}-7 \hat{k})+9}{\sqrt{(5)^{2}+(2)^{2}+(-7)^{2}}}| \\ & =|\frac{5-2-21+9}{\sqrt{25+4+49}}|=|\frac{-9}{\sqrt{78}}| \end{aligned} $

and perpendicular distance of $Q(3 \hat{i}+3 \hat{j}+3 \hat{k})$ from the plane

$ \begin{aligned} & =|\frac{(3 \hat{i}+3 \hat{j}+3 \hat{k}) \cdot(5 \hat{i}+2 \hat{j}-7 \hat{k})+9}{\sqrt{25+4+49}}| \\ & =|\frac{15+6-21+9}{\sqrt{78}}|=|\frac{9}{\sqrt{78}}| \end{aligned} $

Hence, the two points are equidistant from the given plane. Opposite sign shows that they lie on either side of the plane.

Solution

Position vector of $A$ is $6 \hat{i}+7 \hat{j}+4 \hat{k}$ and $\overrightarrow{{}AB}=3 \hat{i}-\hat{j}+\hat{k}$

So, equation of any line passing through $A$ and parallel to $\overrightarrow{{}AB}$

$$ \begin{equation*} \vec{r}=(6 \hat{i}+7 \hat{j}+4 \hat{k})+\lambda(3 \hat{i}-\hat{j}+\hat{k}) \tag{i} \end{equation*} $$

Now any point $P$ on $\overrightarrow{{}AB}=(6+3 \lambda, 7-\lambda, 4+\lambda)$

Similarly, position vector of $C$ is $-9 \hat{j}+2 \hat{k}$

and $\overrightarrow{{}CD}=-3 \hat{i}+2 \hat{j}+4 \hat{k}$

So, equation of any line passing through $C$ and parallel to $\overrightarrow{{}CD}$ is

$$ \begin{equation*} \vec{r}=(-9 j+2 \hat{k})+\mu(-3 \hat{i}+2 \hat{j}+4 \hat{k}) \tag{ii} \end{equation*} $$

Any point $Q$ on $\overrightarrow{{}CD}=(-3 \mu,-9+2 \mu, 2+4 \mu)$

d’ratios of $\overrightarrow{{}PQ}$ are

$ (6+3 \lambda+3 \mu, 7-\lambda+9-2 \mu, 4+\lambda-2-4 \mu) $

$\Rightarrow(6+3 \lambda+3 \mu),(16-\lambda-2 \mu),(2+\lambda-4 \mu)$

Now $\overrightarrow{{}PQ}$ is $\perp$ to eq. (i), then

$3(6+3 \lambda+3 \mu)-1(16-\lambda-2 \mu)+1(2+\lambda-4 \mu)=0$

$\Rightarrow 18+9 \lambda+9 \mu-16+\lambda+2 \mu+2+\lambda-4 \mu=0 $

$\Rightarrow 11 \lambda+7 \mu+4=0\qquad $(iii)

$\overrightarrow{{}PQ} \text{ is also } \perp \text{ to eq. }(\text{ ii }) \text{, then }$

$-3(6+3 \lambda+3 \mu)+2(16-\lambda-2 \mu)+4(2+\lambda-4 \mu)=0 $

$\Rightarrow -18-9 \lambda-9 \mu+32-2 \lambda-4 \mu+8+4 \lambda-16 \mu=0 $

$\Rightarrow -7 \lambda-29 \mu+22=0 $

$\Rightarrow 7 \lambda+29 \mu-22=0 \qquad $(iv)

Solving eq. (iii) and (iv) we get

$ \begin{aligned} 7 \lambda+49 \mu+28=0 \\ 77 \lambda+319 \mu-242=0 \\ (-) \quad (-) \quad (+) \\ \hline -270\mu+270=0 \end{aligned} $

$\therefore \mu=1$

Now using $\mu=1$ in eq. (iv) we get

$ 7 \lambda+29-22=0 \Rightarrow \lambda=-1 $

$\therefore$ Position vector of $P=[6+3(-1), 7+1,4-1]=(3,8,3)$

and position vector of $Q=[-3(1),-9+2(1), 2+4(1)]=(-3,-7,6)$

Hence, the position vectors of

$ P=3 \hat{i}+8 \hat{j}+3 \hat{k} \text{ and } Q=-3 \hat{i}-7 \hat{j}+6 \hat{k} $

Solution

Given that $2 l+2 m-n=0$ and $\quad m n+n l+l m=0$

Eliminating $m$ from eq. (i) and (ii) we get,

$ \begin{aligned} & m=\frac{n-2 l}{2} \\ \Rightarrow & (\frac{n-2 l}{2}) n+n l+l(\frac{n-2 l}{2})=0 \\ \Rightarrow & \frac{n^{2}-2 n l+2 n l+n l-2 l^{2}}{2}=0 \\ \Rightarrow & n^{2}+n l-2 l^{2}=0 \\ \Rightarrow & n^{2}+2 n l-n l-2 l^{2}=0 \\ \Rightarrow & n(n+2 l)-l(n+2 l)=0 \\ \Rightarrow & (n-l)(n+2 l)=0 \\ \Rightarrow & n=-2 l \quad \text{ and } \quad n=l \\ \therefore & m=\frac{-2 l-2 l}{2}, \quad m=\frac{l-2 l}{2} \\ \Rightarrow & m=-2 l, \quad m=\frac{-l}{2} \end{aligned} $

Therefore, the direction ratios are proportional to $l,-2 l,-2 l$ and $l, \frac{-l}{2}, l$.

$\Rightarrow 1,-2,-2$ and $2,-1,2$

If the two lines are perpendicular to each other then

$ \begin{aligned} 1(2)-2(-1)-2 \times 2 & =0 \\ 2+2-4 & =0 \\ 0 & =0 \end{aligned} $

Hence, the two lines are perpendicular.

Solution

Let $\vec{a}, \vec{b}, \vec{c}$ and $\vec{d}$ are such that

$ \vec{a}=l_1 \hat{i}+m_1 \hat{j}+n_1 \hat{k} $

$ \begin{aligned} \vec{b} & =l_2 \hat{i}+m_2 \hat{j}+n_2 \hat{k} \\ \vec{c} & =l_3 \hat{i}+m_3 \hat{j}+n_3 \hat{k} \end{aligned} $

and $\vec{d}=(l_1+l_2+l_3) \hat{i}+(m_1+m_2+m_3) \hat{j}+(n_1+n_2+n_3) \hat{k}$

Since the given $d^{\prime}$ cosines are mutually perpendicular then

$ \begin{aligned} & l_1 l_2+m_1 m_2+n_1 n_2=0 \\ & l_2 l_3+m_2 m_3+n_2 n_3=0 \\ & l_1 l_3+m_1 m_3+n_1 n_3=0 \end{aligned} $

Let $\alpha, \beta$ and $\gamma$ be the angles between $\vec{a}$ and $\vec{d}, \vec{b}$ and $\vec{d}, \vec{c}$ and $\vec{d}$ respectively.

$ \begin{aligned} \therefore \cos \alpha & =l_1(l_1+l_2+l_3)+m_1(m_1+m_2+m_3)+n_1(n_1+n_2+n_3) \\ & =l_1^{2}+l_1 l_2+l_1 l_3+m_1^{2}+m_1 m_2+m_1 m_3+n_1^{2}+n_1 n_2+n_1 n_3 \\ & =(l_1^{2}+m_1^{2}+n_1^{2})+(l_1 l_2+m_1 m_2+n_1 n_2)+(l_1 l_3+m_1 m_3+n_1 n_3) \\ & =1+0+0=1 \\ \therefore \cos \beta & =l_2(l_1+l_2+l_3)+m_2(m_1+m_2+m_3)+n_2(n_1+n_2+n_3) \\ & =l_1 l_2+l_2^{2}+l_2 l_3+m_1 m_2+m_2^{2}+m_2 m_3+n_1 n_2+n_2^{2}+n_2 n_3 \\ & =(l_2^{2}+m_2^{2}+n_2^{2})+(l_1 l_2+m_1 m_2+n_1 n_2)+(l_2 l_3+m_2 m_3+n_2 n_3) \\ & =1+0+0=1 \end{aligned} $

Similarly,

$ \begin{aligned} \therefore \cos \gamma & =l_3(l_1+l_2+l_3)+m_3(m_1+m_2+m_3)+n_3(n_1+n_2+n_3) \\ & =l_1 l_3+l_2 l_3+l_3^{2}+m_1 m_3+m_2 m_3+m_3^{2}+n_1 n_3+n_2 n_3+n_3^{2} \\ & =(l_3^{2}+m_3^{2}+n_3^{2})+(l_1 l_3+m_1 m_3+n_1 n_3)+(l_2 l_3+m_2 m_3+n_2 n_3) \\ & =1+0+0=1 \end{aligned} $

$\therefore \cos \alpha=\cos \beta=\cos \gamma=1 \Rightarrow \alpha=\beta=\gamma$ which is the required result.

Solution

The given point is $(\alpha, \beta, \gamma)$

Any point on $y$-axis $=(0, \beta, 0)$

$\therefore$ Required distance $=\sqrt{(\alpha-0)^{2}+(\beta-\beta)^{2}+(\gamma-0)^{2}}$

$ =\sqrt{\alpha^{2}+\gamma^{2}} $

Hence, the correct option is (d).

• Option (a) $\beta$: This option is incorrect because $\beta$ represents the coordinate of the point along the $y$-axis, not the distance from the $y$-axis. The distance from the $y$-axis depends on the $x$ and $z$ coordinates, not just the $y$ coordinate.

• Option (b) $|\beta|$: This option is incorrect for the same reason as option (a). The absolute value of the $y$ coordinate does not represent the distance from the $y$-axis. The distance is determined by the $x$ and $z$ coordinates.

• Option (c) $|\beta|+|\gamma|$: This option is incorrect because it incorrectly combines the absolute values of the $y$ and $z$ coordinates. The distance from the $y$-axis should be calculated using the Euclidean distance formula, which involves squaring the $x$ and $z$ coordinates, not adding the absolute values of the $y$ and $z$ coordinates.

Solution

If $l, m, n$ are the direction cosines of a line, then

$l^{2}+m^{2}+n^{2} =1 $

$\text{ So, } \quad k^{2}+k^{2}+k^{2} =1 $

$ \quad \Rightarrow 3 k^{2} =1 \Rightarrow k= \pm \frac{1}{\sqrt{3}}$

Hence, the correct option is (d).

• Option (a) $k>0$ is incorrect because the value of $k$ can be either positive or negative. The correct values of $k$ are $\frac{1}{\sqrt{3}}$ or $-\frac{1}{\sqrt{3}}$, so $k$ is not necessarily greater than 0.

• Option (b) $0<k<1$ is incorrect because the value of $k$ can be negative as well. The correct values of $k$ are $\frac{1}{\sqrt{3}}$ or $-\frac{1}{\sqrt{3}}$, and $-\frac{1}{\sqrt{3}}$ does not fall within the range $0<k<1$.

• Option (c) $k=1$ is incorrect because substituting $k=1$ into the equation $3k^2 = 1$ does not satisfy the equation. The correct values of $k$ are $\frac{1}{\sqrt{3}}$ or $-\frac{1}{\sqrt{3}}$.

Solution

Given that: $\vec{r} \cdot(\frac{2}{7} \hat{i}+\frac{3}{7} \hat{j}-\frac{6}{7} \hat{k})=1$

So, the distance of the given plane from the origin is

$\begin{aligned}=|\frac{-1}{\sqrt{(\frac{2}{7})^{2}+(\frac{3}{7})^{2}+(\frac{-6}{7})^{2}}}|=|\frac{-1}{\sqrt{\frac{4}{49}+\frac{9}{49}+\frac{36}{49}}}|=\frac{1}{1}=1\end{aligned}$

Hence, the correct option is $(a)$.

• Option (b) 7 is incorrect because the calculation of the distance involves dividing by the magnitude of the normal vector, which results in a value of 1, not 7.

• Option (c) $\frac{1}{7}$ is incorrect because the correct distance calculation yields a value of 1, not $\frac{1}{7}$.

• Option (d) None of these is incorrect because the correct distance is indeed 1, which matches option (a).

Solution

Given that: $l: \frac{x-2}{3}=\frac{y-3}{4}=\frac{z-4}{5}$

and $\quad P: 2 x-2 y+z=5$

d’ratios of the line are $3,4,5$

and d’ratios of the normal to the plane are $2,-2,1$

$ \begin{matrix} \therefore & \sin \theta=\frac{3(2)+4(-2)+5(1)}{\sqrt{9+16+25} \cdot \sqrt{4+4+1}} \\ \Rightarrow & \sin \theta=\frac{6-8+5}{\sqrt{50} \cdot 3} \Rightarrow \frac{3}{5 \sqrt{2} \cdot 3}=\frac{1}{5 \sqrt{2}}=\frac{\sqrt{2}}{10} \end{matrix} $

Hence, the correct option is $(d)$.

• Option (a) $\frac{10}{6 \sqrt{5}}$: This option is incorrect because the numerator and denominator do not match the correct calculation. The correct numerator should be 3, and the denominator should be $5 \sqrt{2} \cdot 3$. The given option does not simplify to the correct value of $\frac{\sqrt{2}}{10}$.

• Option (b) $\frac{5}{5 \sqrt{2}}$: This option is incorrect because it simplifies to $\frac{1}{\sqrt{2}}$, which is not the correct value. The correct value is $\frac{\sqrt{2}}{10}$, which is different from $\frac{1}{\sqrt{2}}$.

• Option (c) $\frac{2 \sqrt{3}}{5}$: This option is incorrect because the numerator and denominator do not match the correct calculation. The correct numerator should be 3, and the denominator should be $5 \sqrt{2} \cdot 3$. The given option does not simplify to the correct value of $\frac{\sqrt{2}}{10}$.

Solution

Reflection of point $(\alpha, \beta, \gamma)$ in $x y$-plane is $(\alpha, \beta,-\gamma)$.

Hence, the correct option is $(d)$.

• Option (a) $(\alpha, \beta, 0)$ is incorrect because the reflection of a point in the $xy$-plane does not change the $x$ and $y$ coordinates, but it changes the $z$ coordinate to its negative value, not to zero.

• Option (b) $(0,0, \gamma)$ is incorrect because the reflection of a point in the $xy$-plane does not change the $x$ and $y$ coordinates to zero; it only changes the $z$ coordinate to its negative value.

• Option (c) $(-\alpha,-\beta, \gamma)$ is incorrect because the reflection of a point in the $xy$-plane does not change the $x$ and $y$ coordinates to their negative values; it only changes the $z$ coordinate to its negative value.

Solution

Given points are

$A(0,4,1), B(2,3,-1), C(4,5,0)$ and $D(2,6,2)$

d’ratios of $AB=2,-1-2$

and d’ratios of $D C=2,-1,-2$

$\therefore AB | DC$

Similarly, d’ratios of $AD=2,2,1$ and d’ratios of $BC=2,2,1$

$\therefore AD | BC$

So $\square ABCD$ is a parallelogram.

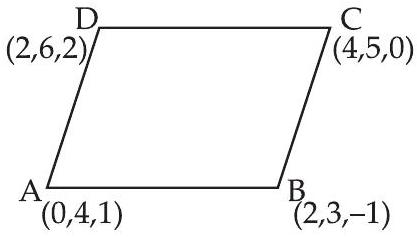
$ \begin{aligned} & \overrightarrow{{}AB}=2 \hat{i}-\hat{j}-2 \hat{k} \\ & \overrightarrow{{}AD}=2 \hat{i}+2 \hat{j}+\hat{k} \end{aligned} $

$\therefore$ Area of parallelogram $ABCD=|\overrightarrow{{}AB} \times \overrightarrow{{}AD}|$

$= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & -1 & -2 \\ 2 & 2 & 1\end{vmatrix} =\hat{i}(-1+4)-\hat{j}(2+4)+\hat{k}(4+2)=3 \hat{i}-6 \hat{j}+6 \hat{k}$

$=\sqrt{(3)^{2}+(-6)^{2}+(6)^{2}}=\sqrt{9+36+36}=\sqrt{81}=9$ sq units

Hence, the correct option is $(a)$.

• Option (b) 18 sq. units: This option is incorrect because the calculated area of the parallelogram $ABCD$ is 9 square units, not 18. The determinant method used to find the area yields a result of 9, which is significantly less than 18.

• Option (c) 27 sq. units: This option is incorrect because the calculated area of the parallelogram $ABCD$ is 9 square units, not 27. The determinant method used to find the area yields a result of 9, which is significantly less than 27.

• Option (d) 81 sq. units: This option is incorrect because the calculated area of the parallelogram $ABCD$ is 9 square units, not 81. The determinant method used to find the area yields a result of 9, which is significantly less than 81.

Solution

Given that: $\quad x y+y z=0$

$ \begin{aligned} y \cdot(x+z) & =0 \\ y & =0 \text{ or } x+z=0 \end{aligned} $

Here $y=0$ is one plane and $x+z=0$ is another plane. So, it is a pair of perpendicular planes.

Hence, the correct option is $(d)$.

• (a) A pair of perpendicular lines: The equation (xy + yz = 0) represents a relationship in three-dimensional space involving planes, not lines. Therefore, it cannot represent a pair of perpendicular lines.

• (b) A pair of parallel lines: Similar to option (a), the equation (xy + yz = 0) involves variables in three-dimensional space and describes planes, not lines. Hence, it cannot represent a pair of parallel lines.

• (c) A pair of parallel planes: The equation (xy + yz = 0) simplifies to (y(x + z) = 0), which gives two distinct planes: (y = 0) and (x + z = 0). These planes intersect along a line and are not parallel to each other. Therefore, it cannot represent a pair of parallel planes.

Solution

Direction ratios of the normal to the plane $2 x-3 y+6 z-11=0$ are 2, -3, 6

Direction ratios of $x$-axis are $1,0,0$ $\therefore$ angle between plane and line is

$ \begin{aligned} \sin \theta & =\frac{2(1)-3(0)+6(0)}{\sqrt{(2)^{2}+(-3)^{2}+(6^{2})} \cdot \sqrt{(1)^{2}+(0)^{2}+(0)^{2}}} \\ & =\frac{2}{\sqrt{4+9+36}}=\frac{2}{7} \end{aligned} $

Hence, the correct option is (c).

• Option (a) $\frac{\sqrt{3}}{2}$: This value is incorrect because it does not match the calculated value of $\frac{2}{7}$ for $\sin \theta$. The calculation involves the dot product of the direction ratios of the normal to the plane and the direction ratios of the x-axis, divided by the product of their magnitudes. The result of this calculation is $\frac{2}{7}$, not $\frac{\sqrt{3}}{2}$.

• Option (b) $\frac{\sqrt{2}}{3}$: This value is incorrect for the same reason as option (a). The correct value of $\sin \theta$ is derived from the specific direction ratios given in the problem, and the result is $\frac{2}{7}$. The value $\frac{\sqrt{2}}{3}$ does not match this result.

• Option (d) $\frac{3}{7}$: This value is also incorrect because the correct calculation yields $\frac{2}{7}$, not $\frac{3}{7}$. The dot product and magnitude calculations specifically result in $\frac{2}{7}$, making $\frac{3}{7}$ an incorrect option.

Solution

Given points are $(2,0,0),(0,3,0)$ and $(0,0,4)$.

So, the intercepts cut by the plane on the axes are 2, 3, 4

Equation of the plane (intercept form) is

$ \frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1 \quad \Rightarrow \quad \frac{x}{2}+\frac{y}{3}+\frac{z}{4}=1 $

Hence, the equation of plane is $\frac{x}{2}+\frac{y}{3}+\frac{z}{4}=1$.

Solution

Let

$ \vec{a}=2 \hat{i}+2 \hat{j}-\hat{k} $

direction ratios of $\vec{a}$ are 2,2 , -1

So, the direction cosines are $\frac{2}{\sqrt{4+4+1}}, \frac{2}{\sqrt{4+4+1}}, \frac{-1}{\sqrt{4+4+1}}$

$\Rightarrow \frac{2}{3}, \frac{2}{3}, \frac{-1}{3}$

Hence, the direction cosines of the given vector are $\frac{2}{3}, \frac{2}{3}, \frac{-1}{3}$.

Solution

The given equation is

$ \frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2} $

Here $\vec{a}=(5 \hat{i}-4 \hat{j}+6 \hat{k})$ and $\vec{b}=(3 \hat{i}+7 \hat{j}+2 \hat{k})$

Equation of the line is $\vec{r}=\vec{a}+\vec{b} \lambda$

Hence, the vector equation of the given line is

$ \vec{r}=(5 \hat{i}-4 \hat{j}+6 \hat{k})+\lambda(3 \hat{i}+7 \hat{j}+2 \hat{k}) $

Solution

Given the points $(3,4,-7)$ and $(1,-1,6)$

Here $\vec{a}=3 \hat{i}+4 \hat{j}-7 \hat{k}$ and $\vec{b}=\hat{i}-\hat{j}+6 \hat{k}$

Equation of the line is $\vec{r}=\vec{a}+\lambda(\vec{b}-\vec{a})$

$\Rightarrow \vec{r}=(3 \hat{i}+4 \hat{j}-7 \hat{k})+\lambda[(\hat{i}-\hat{j}+6 \hat{k})-(3 \hat{i}+4 \hat{j}-7 \hat{k})]$

$\Rightarrow \vec{r}=(3 \hat{i}+4 \hat{j}-7 \hat{k})+\lambda(-2 \hat{i}-5 \hat{j}+13 \hat{k})$

$\Rightarrow(x \hat{i}+y \hat{j}+z \hat{k})=(3 \hat{i}+4 \hat{j}-7 \hat{k})+\lambda(-2 \hat{i}-5 \hat{j}+13 \hat{k})$

$\Rightarrow(x-3) \hat{i}+(y-4) \hat{j}+(z+7) \hat{k}=\lambda(-2 \hat{i}-5 \hat{j}+13 \hat{k})$

Hence, the vector equation of the line is

$ (x-3) \hat{i}+(y-4) \hat{j}+(z+7) \hat{k}=\lambda(-2 \hat{i}-5 \hat{j}+13 \hat{k}) $

Solution

Given equation is $\vec{r} \cdot(\hat{i}+\hat{j}-\hat{k})=2$

$\begin{matrix} \Rightarrow & (x \hat{i}+y \hat{j}+z \hat{k}) \cdot(\hat{i}+\hat{j}-\hat{k}) & =2 \\ \Rightarrow & x+y-z & =2\end{matrix} $

Hence, the Cartesian equation of the plane is $x+y-z=2$.

Solution

Given plane is $x+2 y+3 z-6=0$

Vector normal to the plane $\vec{n}=\hat{i}+2 \hat{j}+3 \hat{k}$

$\therefore \hat{n}=\frac{\vec{n}}{|\vec{n}|}=\frac{\hat{i}+2 \hat{j}+3 \hat{k}}{\sqrt{(1)^{2}+(2)^{2}+(3)^{2}}}=\frac{1}{\sqrt{14}} \hat{i}+\frac{2}{\sqrt{14}} \hat{j}+\frac{3}{\sqrt{14}} \hat{k}$

Hence, the given statement is ’true'.

Solution

Equation of the plane is $2 x-3 y+5 z+4=0$

$\Rightarrow \quad 2 x-3 y+5 z=-4$

$\Rightarrow \frac{2}{-4} x-\frac{3 y}{-4}+\frac{5 z}{-4}=1$

$\Rightarrow \frac{x}{-2}-\frac{y}{4 / 3}+\frac{z}{-4 / 5}=1$

So, the required intercepts are $-2, \frac{4}{3}$ and $-\frac{4}{5}$

Hence, the given statement is ’true'.

Solution

Equation of line is $\vec{r}=(5 \hat{i}-\hat{j}-4 \hat{k})+\lambda(2 \hat{i}-\hat{j}+\hat{k})$ and the equation of the plane is $\vec{r} \cdot(3 \hat{i}-4 \hat{j}-\hat{k})+5=0$

Here, $ \vec{b} _1=2 \hat{i}-\hat{j}+\hat{k}$ and $ \vec{n} _2=3 \hat{i}-4 \hat{j}-\hat{k}$

$\therefore \quad \sin \theta=\frac{b_1 \vec{n} _2}{| \vec{b} _1|| \vec{n} _2|}$

$\Rightarrow \quad \sin \theta=\frac{(2 \hat{i}-\hat{j}+\hat{k}) \cdot(3 \hat{i}-4 \hat{j}-\hat{k})}{\sqrt{4+1+1} \cdot \sqrt{9+16+1}}=\frac{6+4-1}{\sqrt{6} \cdot \sqrt{26}}=\frac{9}{\sqrt{6} \cdot \sqrt{26}}$

$\Rightarrow \quad \sin \theta=\frac{9}{2 \sqrt{39}}$ which is false.

Hence, the given statement is ‘false’.

Solution

The given planes are $\vec{r} \cdot(2 \hat{i}-3 \hat{j}+\hat{k})=1$ and $\vec{r} \cdot(\hat{i}-\hat{j})=4$

Here, $ \vec{b} _1=2 \hat{i}-3 \hat{j}+\hat{k}$ and $ \vec{b} _2=(\hat{i}-\hat{j})$

So, $\quad \cos \theta=\frac{ \vec{b} _1 \cdot \vec{n} _2}{| \vec{b} _1|| \vec{n} _2|}$

$\Rightarrow \quad \cos \theta=\frac{(2 i-3 j+\hat{k}) \cdot(\hat{i}-\hat{j})}{\sqrt{4+9+1} \cdot \sqrt{1+1}}=\frac{2+3}{\sqrt{14} \cdot \sqrt{2}}=\frac{5}{\sqrt{28}}$

$\therefore \quad \theta=\cos ^{-1}(\frac{5}{\sqrt{28}})$ which is false.

Hence, the given statement is ‘false’.

Solution

Direction ratios of the line $(\hat{i}-\hat{j}+2 \hat{k})$

Direction ratios of the normal to the plane are $(3 \hat{i}+\hat{j}-\hat{k})$

So $(\hat{i}-\hat{j}+2 \hat{k}) \cdot(3 \hat{i}+\hat{j}-\hat{k})=3-1-2=0$

Therefore, the line is parallel to the plane.

Now point through which the line is passing

$\vec{a}=2 \hat{i}-3 \hat{j}-\hat{k}$

If line lies in the plane then

$ \begin{matrix} (2 \hat{i}-3 \hat{j}-\hat{k}) \cdot(3 \hat{i}+\hat{j}-\hat{k})+2=0 \\ 6-3+1+2 \neq 0 \end{matrix} $

So, the line does not lie in the plane.

Hence, the given statement is ‘false’.

Solution

The Cartesian form of the equation is

$\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}=\lambda$

$\therefore$ Here $x_1=5, y_1=-4, z_1=6, a=3, b=7, c=2$

So, the vector equation is $\vec{r}=(5 \hat{i}-4 \hat{j}+6 \hat{k})+\lambda(3 \hat{i}+7 \hat{j}+2 \hat{k})$

Hence, the given statement is ’true'.

Solution

Here, $x_1=5, y_1=-2, z_1=4 ; a=2, b=1, c=3$

We know that the equation of line is $\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}$

$\Rightarrow \quad \frac{x-5}{2}=\frac{y+2}{1}=\frac{z-4}{3}$

Hence, the given statement is ‘false’.

Solution

The given equation of the plane is $\vec{r} .(5 \hat{i}-3 \hat{j}-2 \hat{k})=38$

If the foot of the perpendicular to this plane is

$(5,-3,-2)$ i.e., $5 \hat{i}-3 \hat{j}-2 \hat{k}$ then

$(5 \hat{i}-3 \hat{j}-2 \hat{k}) \cdot(5 \hat{i}-3 \hat{j}-2 \hat{k})=38$

$\Rightarrow \quad 25+9+4=38$

$38=38$ (satisfied)

Hence, the given statement is ’true'.