Basic concepts

Circle : A circle is the locus of points which are equidistant from a fixed point and lies on the same plane.

Fixed point is called centre of a circle and constant distance is called radius of the circle

Standard equation of a circle

The equation of a circle with the centre at $(\mathrm{h}, \mathrm{k})$ and radiaus $\mathrm{r}$ is

$ (\mathrm{x}-\mathrm{h})^{2}+(\mathrm{y}-\mathrm{k})^{2}=\mathrm{r}^{2} $

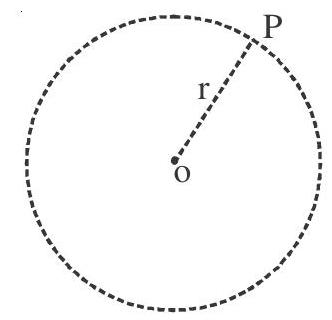
If centre is at the origin and radius is $r$ then the equation of circle is $x^{2}+y^{2}$ $=\mathrm{r}^{2}$

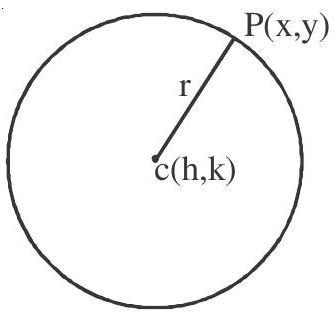
General equation of a circle

$x^{2}+y^{2}+2 g x+2 f y+c=0$ where $g, f$, and $c$ are constants

centre ( $-\mathrm{g},-\mathrm{f})$ and radius is $\sqrt{\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{c}}$

Conditions for a second-degree equation to represent a circle

$a^{2}+2 h x y+b y^{2}+2 g x+2 f y+c=0$ is a second degree equation

(i) coefficient of $\mathrm{x}^{2}=$ coefficient of $\mathrm{y}^{2} . \quad$ ie., $\quad \mathrm{a}=\mathrm{b}$

(ii) coefficient of $x y=0 \quad\quad\quad\quad\quad\quad$ ie., $\quad \mathrm{h}=0$

If $\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{c}>0$ then the circle represents real circle with centre $(-\mathrm{g},-\mathrm{f})$

If $\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{c}=0$ then the circle represents point circle since radius is zero

If $\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{c}<0$ then the circle is imaginary circle .

Equation of circle in various forms

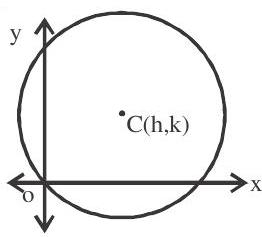
1. Equation of circle with centre (h.k) and passes through origin. is $x^{2}+y^{2}+2 h x+2 k y=0$

Note that when a circle passes through origin the constant term must be zero

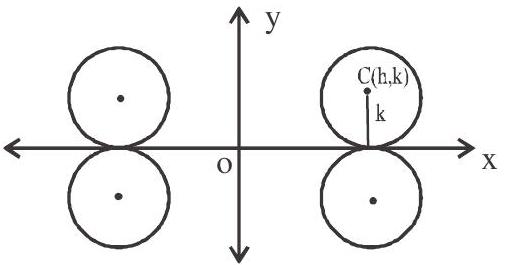
2. If the circle touches $\mathrm{x}$-axis then its equation is $(\mathrm{x} \pm \mathrm{h})^{2}+(\mathrm{y} \pm \mathrm{k})^{2}=\mathrm{k}^{2}(\mathrm{or}) \mathrm{x}^{2}+\mathrm{y}^{2} \pm 2 \mathrm{hx} \pm 2 \mathrm{ky}+\mathrm{h}^{2}=0$. In this case radius is ordinate of centre of a circle. Four circles possible

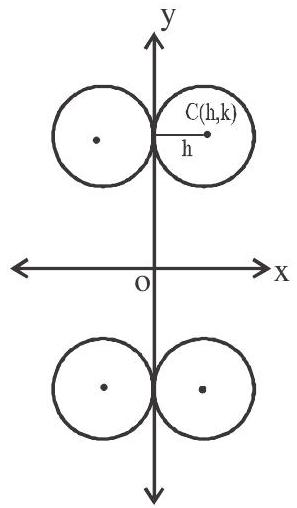
3. If the circle touches $y$-axis then its equation is $(x \pm h)^{2}+(y \pm k)^{2}=h^{2}($ or $) x^{2}+y^{2} \pm 2 h x \pm 2 k y+k^{2}$ $=0$. Here radius of the circle is abscissa of the centre. Four circles possible.

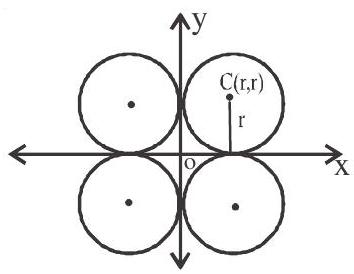
4. If the circle touches both the axes then its equation is $(x \pm r)^{2}+(y \pm r)^{2}=r^{2}$. Four circles possible $\mathrm{x}^{2}+\mathrm{y}^{2} \pm 2 \mathrm{rx} \pm 2 \mathrm{ry}+\mathrm{r}^{2}=0$

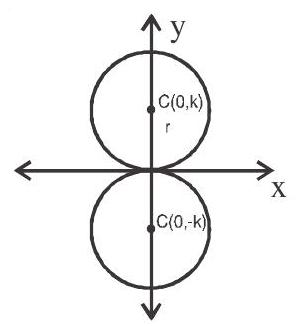
5. If the circle touches $x$-axis at origin then its equation is $x^{2}+(y \pm k)^{2}=k^{2}$

$\mathrm{x}^{2}+\mathrm{y}^{2} \pm 2 \mathrm{ky}=0$

6. If the circle touches $y$-axis at origin then its equation is $(x \pm h)^{2}+y^{2}=h^{2}(o r) x^{2}+y^{2} \pm 2 h x=0$

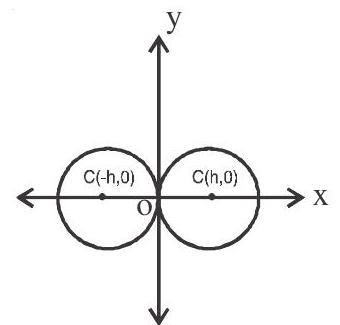
7. If the circle passes through origin and cuts intercepts $a$ and $b$ on the axes, then the equation of circle is $\mathrm{x}^{2}+\mathrm{y}^{2}-\mathrm{ax}-\mathrm{by}=0$ and centre is $\mathrm{c}(\mathrm{a} / 2, \mathrm{~b} / 2)$ four circles possible.

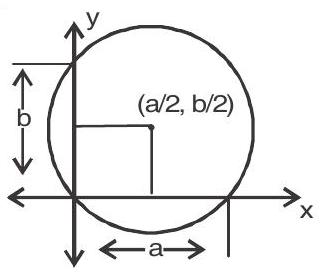
Equation of circle on a given diameter

8. If $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ and $\left(\mathrm{x} _{2}, \mathrm{y} _{2}\right)$ are end points of the diameter then the equation of circle is $\left(\mathrm{x}-\mathrm{x} _{1}\right)\left(\mathrm{x}-\mathrm{x} _{2}\right)+\left(\mathrm{y}-\mathrm{y} _{1}\right)\left(\mathrm{y}-\mathrm{y} _{2}\right)=0$

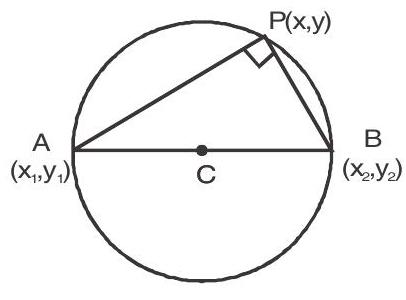
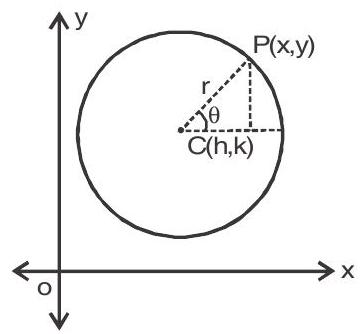
Parametric form of circle

9. $\mathrm{x}=\mathrm{h}+\mathrm{r} \cos \theta$

$\mathrm{y}=\mathrm{k}+\mathrm{r} \sin \theta$

Where $\theta$ is parameter $(0 \leq \theta \leq 2 \pi)$

In particular coordinates of any point on the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{r}^{2}$ is $(\mathrm{r} \cos \theta, r \sin \theta)$ on the circle $\mathrm{x}^{2}+\mathrm{y}^{2}+2 \mathrm{gx}+2 \mathrm{fy}+\mathrm{c}=0$ is $\left(-\mathrm{g}+\sqrt{\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{c}}(\cos \theta),-f+\sqrt{\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{c}}(\sin \theta)\right)$

Intercept made on the axes by a circle

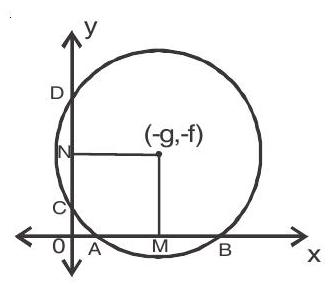
10. Let the equation of circle is $x^{2}+y^{2}+2 g x+2 f y+c=0$

$\mathrm{AB}=\mathrm{x}-$ intercept $=2 \sqrt{\mathrm{g}^{2}-\mathrm{c}}$

$\mathrm{CD}=\mathrm{y}-$ intercept $=2 \sqrt{\mathrm{f}^{2}-\mathrm{c}}$