CIRCLE-5 (Tangents and Normals)
1. Chord of contact
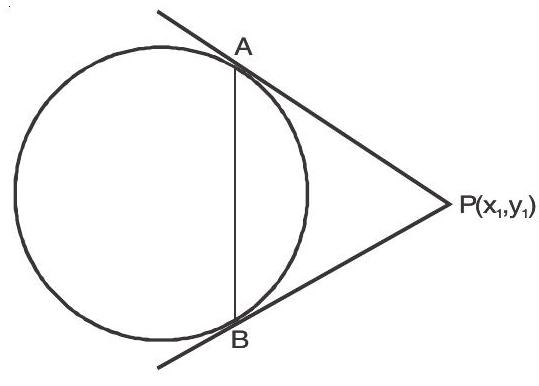
Let the equation of circle be $x^{2}+y^{2}=\underline{r}^{2}$ PA and $\mathrm{PB}$ are pair of tangents drawn from the point $\mathrm{P}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ then $\mathrm{AB}$ is the chord of contact with $\mathrm{A}$ and $B$ as its points of contact.
$\therefore$ Equation of chord of contact $\mathrm{AB}$ is $\mathrm{xx} _{1}+\mathrm{yy} _{1}=\underline{a}^{2}$ Equation of chord of contact look like equation of tangent at point but point are different
If the equation of circle be $x^{2}+y^{2}+2 g x+2 f y+c= 0$ then the equation of chord of contact is $\mathrm{xx} _{1}+\mathrm{yy} _{1}+\mathrm{g}\left(\mathrm{x}+\mathrm{x} _{1}\right)+\mathrm{f}\left(\mathrm{y}+\mathrm{y} _{1}\right)+\mathrm{c}=0$
2. Equation of the chord bisected at a given point
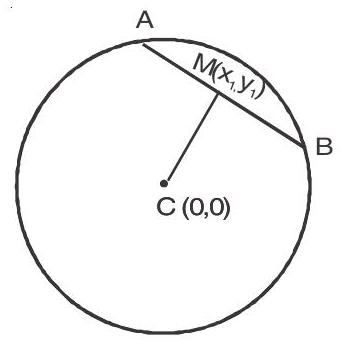
Let the equation of circle be $x^{2}+y^{2}=r^{2}$ and $A B$ is a chord of it $\operatorname{Let}\left(M\left(x _{1}, y _{1}\right)\right.$ be midpoint of $A B$.
$ \begin{aligned} & \text { Slope of } C M=\frac{y _{1}}{x _{1}} \\ & \text { Slope of } A B=\frac{-x _{1}}{y _{1}} \end{aligned} $
Equation of chord $\mathrm{AB}$ is
$ \begin{aligned} & \mathrm{y}-\mathrm{y} _{1}=\frac{-\mathrm{x} _{1}}{\mathrm{y} _{1}}\left(\mathrm{x}-\mathrm{x} _{1}\right) \\ & \mathrm{yy} _{1}-\mathrm{y} _{1}^{2}=-\mathrm{xx} _{1}+\mathrm{x} _{1}^{2} \\ & \mathrm{xx} _{1}+\mathrm{yy} _{1}=\mathrm{x} _{1}^{2}+\mathrm{y} _{1}^{2} \\ & \mathrm{xx} _{1}+\mathrm{yy} _{1}-\mathrm{a}^{2}=\mathrm{x} _{1}^{2}+\mathrm{y} _{1}^{2}-\mathrm{a}^{2} \\ & \mathrm{~T}=\mathrm{S} _{1} \end{aligned} $
If the equation of circle be $x^{2}+y^{2}+2 g x+2 f y+c=0$ then the equation of chord which is bisected at $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ is
$\mathrm{xx} _{1}+\mathrm{yy} _{1}+\mathrm{g}\left(\mathrm{x}+\mathrm{x} _{1}\right)+\mathrm{f}\left(\mathrm{y}+\mathrm{y} _{1}\right)+\mathrm{c}=\mathrm{x} _{1}^{2}+\mathrm{y} _{1}{ }^{2}+2 \mathrm{gx} _{1}+2 \mathrm{fy} _{1}+\mathrm{c}$
Examples
1. Find the equation of tangent to the circle $\mathrm{x}^{2}+\mathrm{y}^{2}-2 \mathrm{ax}=0$ at the point $(\mathrm{a}(1+\cos \alpha)$, $\mathrm{sin} \alpha)$
Show Answer
Solution :
Equation of tangent of $x^{2}+y^{2}-2 a x=0 a t(a(1+\cos \alpha)$,asin $\alpha)$ is
$\mathrm{ax}(1+\cos \alpha)+\mathrm{aysin} \alpha-\mathrm{a}(\mathrm{x}+\mathrm{a}(1+\cos \alpha))=0$
$\mathrm{ax}+\mathrm{axcos} \alpha+\mathrm{aysin} \alpha-\mathrm{ax}-\mathrm{a}^{2}(1+\cos \alpha)=0$
$\operatorname{axcos} \alpha+\mathrm{aysin} \alpha=\mathrm{a}^{2}(1+\cos \alpha)$
$\mathrm{x} \cos \alpha+\mathrm{y} \sin \alpha=\mathrm{a}(1+\cos \alpha)$
2. Find the equations of the tangents to the circle $x^{2}+y^{2}=9$ which make an angle of $60^{\circ}$ with the axis.
Show Answer
Solution :
Since tangents make an angle of $60^{\circ}$ with the $\mathrm{x}$-axis so slope of tangent
$\mathrm{m}=\tan 60^{\circ}=\mathrm{m}=\sqrt{3}$
radius of circle $\mathrm{x}^{2}+\mathrm{y}^{2}=9$ is 3
we know equation of tangent to a circle $x^{2}+y^{2}=a^{2}$ is
$y=m x \pm a \sqrt{1+m^{2}}$
$\therefore \mathrm{y}=\sqrt{3} \mathrm{x} \pm 3 \sqrt{1+3}$
$=\sqrt{3} \mathrm{x} \pm 6$
or $\sqrt{3} x-y \pm 6=0$ ie., $\sqrt{3} x-y+6=0$ and $\sqrt{3} x-y-6=0$ are equations of tangents.
3. Show that the line $(\mathrm{x}-2) \cos \theta+(\mathrm{y}-2) \sin \theta=1………(1)$ touches a circle for all values of $\theta$. Find the circle.
Show Answer
Solution :
Since the line $(\mathrm{x}-2) \cos \theta+(\mathrm{y}-2) \sin \theta=1$ (1) touches a circle so it is a tangent equation to a circle.
Equation of tangent to a circle at $\left(x _{1}, y _{1}\right)$ is $(x-h) x _{1}+(y-k) y _{1}=a^{2}$ to a circle $(x-h)^{2}+(y-k)^{2}=a^{2}$ comparing (1) and (2) we get
$\mathrm{x}-\mathrm{h}=\mathrm{x}-2 \quad \mathrm{y}-\mathrm{k}=\mathrm{y}-2 \quad$ and $\mathrm{a}^{2}=1$
$\mathrm{x} _{1}=1 \cos \theta$ $\mathrm{y} _{1}=1 \sin \theta$
$\therefore$ Required equation of circle is
$(\mathrm{x}-2)^{2}+(\mathrm{y}-2)^{2}=1$
$\mathrm{x}^{2}+\mathrm{y}^{2}-4 \mathrm{x}-4 \mathrm{y}+7=0$
4. Find the equation of the normal to the circle $x^{2}+y^{2}=2 x$ which is parallel to the line $x+2 y=3$
Show Answer
Solution :
Equation of normal at $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ of $\mathrm{x}^{2}+\mathrm{y}^{2}-2 \mathrm{x}=0$ is
$\frac{x-x _{1}}{x _{1}-1}=\frac{y-y _{1}}{y _{1}-0}\left(\frac{x-x _{1}}{a x _{1}+g}=\frac{y-y _{1}}{b y _{1}+f}\right)$
Slope of this equation is $\frac{y _{1}}{x _{1}-1}$
Slope of $x+2 y=3$ is $\frac{-1}{2}$
Since given that normal is parallel to $x+2 y=3$
$\therefore \frac{\mathrm{y} _{1}}{\mathrm{x} _{1}-1}=\frac{-1}{2}$
$2 \mathrm{y} _{1}=-\mathrm{x} _{1}+1$ therefore locus of $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ is $\mathrm{x} _{1}+2 \mathrm{y} _{1}=1$
It is the equation of normal $\Rightarrow(x+2 y)=1$
5. Show that the line $3 x-4 y=1$ touches the circle $x^{2}+y^{2}-2 x+4 y+1=0$ find the coordinates of the point of contact.
Show Answer
Solution :
Centre and radius of circle $x^{2}+y^{2}-2 x+4 y+1=0$
is $(1,-2)$ and $\sqrt{1+4-1}=2$ respectively.
If the distance of a line $3 x-4 y=1$ from the centre $(1,-2)$ is equal to radius then the line touches or it is tangent to a circle.
$=\left|\frac{3 \times 1-4(-2)-1}{\sqrt{3^{2}+4^{2}}}\right| \quad\left(\left|\frac{\mathrm{ax} _{1}+\mathrm{by} _{1}+\mathrm{c}}{\sqrt{\mathrm{a}^{2}+\mathrm{b}^{2}}}\right|=\mathrm{d}\right)$
$=\left|\frac{3+8-1}{5}\right|$
$=2$
$\therefore$ line $3 x-4 y=1$ touches the circle.
Let point of contact be $\left(x _{1}, y _{1}\right)$ then equation of tangent to a circle $x^{2}+y^{2}-2 x+4 y+1=0$ is
$\mathrm{xx} _{1}+\mathrm{yy} _{1}-\left(\mathrm{x}+\mathrm{x} _{1}\right)+2\left(\mathrm{y}+\mathrm{y} _{1}\right)+1=0……….(1)$
$\mathrm{x}\left(\mathrm{x} _{1}-1\right)+\mathrm{y}\left(\mathrm{y} _{1}+2\right)-\mathrm{x} _{1}+2 \mathrm{y} _{1}+1=0……..(2)$
and given line $3 x-4 y-1=0$
(1) and (2) are idenfical then comparing (1) and (2) we get
$\frac{\mathrm{x} _{1}-1}{3}=\frac{\mathrm{y} _{1}+2}{-4}=\frac{-\mathrm{x} _{1}+2 \mathrm{y} _{1}+1}{-1}$
$-\mathrm{x} _{1}+1=-3 \mathrm{x} _{1}+6 \mathrm{y} _{1}+3 \quad$ or $\quad 2 \mathrm{x} _{1}-6 \mathrm{y} _{1}-2=0$
$-\mathrm{y} _{1}-2=4 \mathrm{x} _{1}-8 \mathrm{y} _{1}-4 \quad$ or $\quad 4 \mathrm{x} _{1}-7 \mathrm{y} _{1}-2=0$
Solving these two equations of $\mathrm{x} _{1}, \mathrm{y} _{1}$ we get $\mathrm{x} _{1}=\frac{-1}{5}$ and $\mathrm{y} _{1}=\frac{-2}{5}$
$\therefore$ point of contact is $\left(\frac{-1}{5}, \frac{-2}{5}\right)$
6. The angle between a pair of tangents from a point $\mathrm{P}$ to the circle
$x^{2}+y^{2}+4 x-6 y+9 \sin ^{2} \alpha+13 \cos ^{2} \alpha=0$ is $2 \alpha$. Find the equation of the locus of the point $P$.
Show Answer
Solution :
Let the coordinate of $\mathrm{Pbe}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ and given circle is $\mathrm{x}^{2}+\mathrm{y}^{2}+4 \mathrm{x}-6 \mathrm{y}+9 \sin ^{2} \alpha+13 \cos ^{2} \alpha=0$
$(\mathrm{x}+2)^{2}+(\mathrm{y}-3)^{2}-4-9+9 \sin ^{2} \alpha+13 \cos ^{2} \alpha=0$
$(x+2)^{2}+(y-3)^{2}-9 \sin ^{2} \alpha-13\left(1-\cos ^{2} \alpha\right)=0$
$(x+2)^{2}+(y-3)^{2}-9 \sin ^{2} \alpha-13 \sin ^{2} \alpha=0$
$(x+2)^{2}+(y-3)^{2}=4 \sin ^{2} \alpha=(2 \sin \alpha)^{2}$
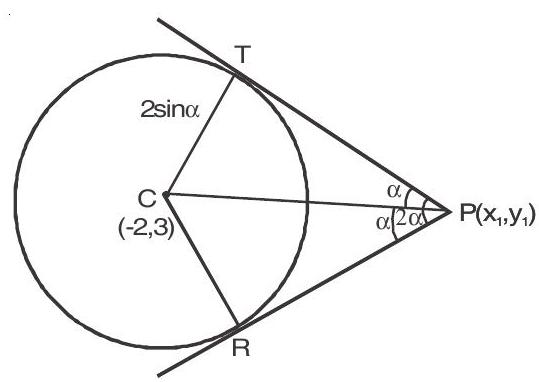
$\therefore$ centre and radius of circle is $(-2,3)$ and $2 \sin \alpha$ respectively
Distance of $\mathrm{P}$ and $\mathrm{C}$ is
$\mathrm{PC}=\sqrt{\left(\mathrm{x} _{1}+2\right)^{2}+\left(\mathrm{y} _{1}-3\right)^{2}}$
In ${ } _{\Delta} \mathrm{PCR}$
$\sin \alpha=\frac{2 \sin \alpha}{\sqrt{\left(\mathrm{x} _{1}+2\right)^{2}+\left(\mathrm{y} _{1}-3\right)^{2}}}$
or $\sqrt{\left(x _{1}+2\right)^{2}+\left(y _{1}-3\right)^{2}}=2$
Squaring
$\left(\mathrm{x} _{1}+2\right)^{2}+(\mathrm{y}-3)^{2}=4$ or $(\mathrm{x}+2)^{2}+(\mathrm{y}-3)^{2}=4$
$\therefore$ locus of point $P$ is a circle
7. If the length of tangent from ( $\mathrm{f}, \mathrm{g})$ to the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=6$ be twice the length of the tangent from (f,g) to circle $x^{2}+y^{2}+3 x+3 y=0$ then prove that $f^{2}+g^{2}+4 f+4 g+2=0$
Show Answer
Solution :
According to the question
$\sqrt{\mathrm{f}^{2}+\mathrm{g}^{2}-6}=2 \sqrt{\mathrm{f}^{2}+\mathrm{g}^{2}+3 \mathrm{f}+3 \mathrm{~g}}$
Squaring both side
$\mathrm{f}^{2}+\mathrm{g}^{2}-6=4\left(\mathrm{f}^{2}+\mathrm{g}^{2}+3 \mathrm{f}+3 \mathrm{~g}\right)$
$3 \mathrm{f}^{2}+3 \mathrm{~g}^{2}+12 \mathrm{f}+12 \mathrm{~g}+6=0$
Divide by 3 we get $\mathrm{f}^{2}+\mathrm{g}^{2}+4 \mathrm{f}+4 \mathrm{~g}+2=0$
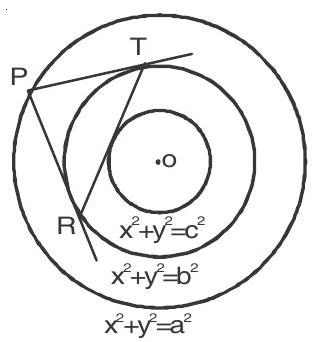
8. The chord of contact of tangents drawn from a point on the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{a}^{2}$ to the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=$ $\mathrm{b}^{2}$ touches the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{c}^{2}$ show that $\mathrm{a}, \mathrm{b}, \mathrm{c}$ are in GP.
Show Answer
Solution :
Let $\mathrm{P}(\mathrm{a} \cos \theta, \operatorname{asin} \theta)$ be a point on the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{a}^{2}$ Then equation of chord of contact to the circle $x^{2}+y^{2}=b^{2}$ from $P(a \cos \theta$, asin $\theta)$ is
$x(a \cos \theta)+y(a \sin \theta)=b^{2}$
$\operatorname{axsin} \theta+a y \sin \theta=b^{2}$
It is a tangent to the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{c}^{2}$
$\therefore$ length of perpendicular to the line $=$ radius.
$\left|\frac{-\mathrm{b}^{2}}{\sqrt{\mathrm{a}^{2}}}\right|=\mathrm{c}$
$\mathrm{b}^{2}=\mathrm{ac}$
$\therefore$ a, b.c are in G.P.