CIRCLE-7 (Intersection of Two Circles)
Angle of intersection of two circles
Let the two circles $S \equiv x^{2}+y^{2}+2 g x+2 f y+c=0$ and $S^{\prime} \equiv x^{2}+y^{2}+2 g _{1} x+2 f _{1} y+c _{1}=0$ intersect each other at the point $\mathrm{P}$ and $\mathrm{Q}$. The angle $\theta$ between two circles $\mathrm{S}=0$ and $\mathrm{S}^{\prime}=0$ is defined as the angle between the tangents to the two circles at the point of intersection. $\theta$ must be taken acute angle .
$C _{1}$ and $C _{2}$ are the centres of circles $S=0$ and $S^{\prime}=0$ then $C _{1}(-g,-f)$ and $C _{2}\left(-g _{1},-f _{1}\right)$ and their radii
$\mathrm{r} _{1}=\sqrt{\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{c}} \& \mathrm{r} _{2}=\sqrt{\mathrm{g} _{1}^{2}+\mathrm{f} _{1}^{2}-\mathrm{c} _{1}}$
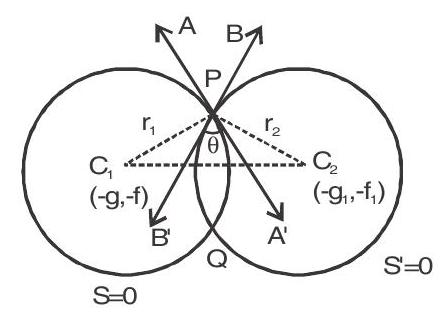
Let $\mathrm{d}=\left|\mathrm{c} _{1} \mathrm{c} _{2}\right|=\sqrt{\left(\mathrm{g}-\mathrm{g} _{1}\right)^{2}+\left(\mathrm{f}-\mathrm{f} _{1}\right)^{2}}=\sqrt{\mathrm{g}^{2}+\mathrm{g} _{1}{ }^{2}-2 \mathrm{gg} _{1}+\mathrm{f}^{2}+\mathrm{f} _{1}{ }^{2}-2 \mathrm{ff} _{1}}$
$\mathrm{C} _{1} \mathrm{P} \perp \mathrm{AA}^{\prime}, \mathrm{C} _{2} \mathrm{P} \perp \mathrm{BB}^{\prime}$ since radius is perpendicular to the tangent at the point of contact ie. $\angle \mathrm{C} _{1} \mathrm{PA}^{\prime}=90^{\circ}$ and $\angle \mathrm{C} _{2} \mathrm{~PB}^{\prime}=90^{\circ}$
$\therefore \angle \mathrm{C} _{1} \mathrm{~PB}^{\prime}=90^{\circ}-\theta$ and $\angle \mathrm{C} _{2} \mathrm{PA}^{\prime}=90^{\circ}-\theta$
Hence $\angle \mathrm{C} _{1} \mathrm{PC} _{2}=90^{\circ}-\theta+\theta+90^{\circ}-\theta=180^{\circ}-\theta$
Now in $\Delta \mathrm{C} _{1} \mathrm{PC} _{2}$
$\cos \left(180^{\circ}-\theta\right)=\frac{\mathrm{r} _{1}{ }^{2}+\mathrm{r} _{2}{ }^{2}-\mathrm{d}^{2}}{2 \mathrm{r} _{1} \mathrm{r} _{2}}$ (cosine rule)
$\cos \theta=\left|\frac{\mathrm{r} _{1}{ }^{2}+\mathrm{r} _{2}{ }^{2}-\mathrm{d}^{2}}{2 \mathrm{r} _{1} \mathrm{r} _{2}}\right|$
If the angle between the circles is $90^{\circ}$ ie., $\theta=90^{\circ}$, then $\cos 90^{\circ}=0$ Then the circles are said to be orthogonal circles or the circles cut each other orthogonally.
$\therefore \mathrm{r} _{1}{ }^{2}+\mathrm{r} _{2}{ }^{2}-\mathrm{d}^{2}=0$
$\mathrm{g}^{2}+\mathrm{f}^{2}-\mathrm{c}^{2}+\mathrm{g} _{1}{ }^{2}+\mathrm{f} _{1}^{2}-\mathrm{c} _{1}-\mathrm{g}^{2}-\mathrm{g} _{1}{ }^{2}+2 \mathrm{gg} _{1}-\mathrm{f}^{2}-\mathrm{f} _{1}{ }^{2}+2 \mathrm{ff} _{1}=0$
$2 \mathrm{gg} _{1}+2 \mathrm{ff} _{1}=\mathrm{c}+\mathrm{c} _{1}$
It is a condition for two circles to be orthogonal
Examples :
1. Find the angle between the circles
$S \equiv x^2+y^2-4 x+6 y+11=0$ and $S^{\prime}=x^2+y^2-2 x+8 y+13=0$
Show Answer
Solution:
Here $S \equiv x^{2}+y^{2}-4 x+6 y+11=0$ and $S^{\prime}=x^{2}+y^{2}-2 x+8 y+13=0$
The centre of these circles are $\mathrm{C} _{1}(2,-3)$ and $\mathrm{C} _{2}(1,-4)$ respectively.
The radius of these circles are $r _{1}=\sqrt{4+9-11}=\sqrt{2}$
and $\mathrm{r} _{2}=\sqrt{1+16-13}=2$
Distance between the centres $\mathrm{C} _{1} \mathrm{C} _{2}=\mathrm{d}=\sqrt{1^{2}+1^{2}}=\sqrt{2}$
Angle between two circle is $\cos \theta=\left|\frac{\mathrm{r} _{1}{ }^{2}+\mathrm{r} _{2}{ }^{2}-\left(\mathrm{c} _{1} \mathrm{c} _{2}\right)^{2}}{2 \mathrm{r} _{1} \mathrm{r} _{2}}\right|=\left|\frac{2+4-2}{2 \times 2 \times \sqrt{2}}\right|=\frac{1}{\sqrt{2}}=\cos \frac{\pi}{4}$
$\therefore \theta=\frac{\pi}{4}$
2. Find the equations of the two circles which intersect the circles $x^{2}+y^{2}-6 y+1=0$ and $x^{2}+y^{2}-$ $4 y+1=0$ orthogonally and touch the line $3 x+4 y+5=0$
Show Answer
Solution:
Let the required equation of circle be $x^{2}+y^{2}+2 g x+2 f y+c=0$
This circle intersect orthogonally with circles $x^{2}+y^{2}-6 y+1=0$ and $x^{2}+y^{2}-4 y+1=0$
Condition for orthogonality is $2 \mathrm{gg} _{1}+2 \mathrm{ff} _{1}=\mathrm{c}+\mathrm{c} _{1}$ $\therefore 0+2 \mathrm{f}(-3)=\mathrm{C}+1 \quad$ and $0+2 \mathrm{f}(-2)=\mathrm{c}+1$ $-6 \mathrm{f}=\mathrm{c}+1$ $-4 \mathrm{f}=\mathrm{c}+1$
$\therefore-6 \mathrm{f}=-4 \mathrm{f} \Rightarrow \mathrm{f}=0$ and $\mathrm{c}=-1$
Equation of circle is $x^{2}+y^{2}+2 g x-1=0$
Centre is $(-\mathrm{g}, 0)$ and radius $\sqrt{\mathrm{g}^{2}+1}$
Since the line $3 x+4 y+5=0$ touches the circle
$\therefore$ distance of this line from the centre must be equal to radius $\sqrt{\mathrm{g}^{2}+1}$
$\therefore\left|\frac{-3 \mathrm{~g}+5}{\sqrt{9+16}}\right|=\sqrt{\mathrm{g}^{2}+1}$
$5-3 \mathrm{~g}=5 \sqrt{\mathrm{g}^{2}+1}$
squaring
$25+9 \mathrm{~g}^{2}-30 \mathrm{~g}=25 \mathrm{~g}^{2}+25$
$16 \mathrm{~g}^{2}+30 \mathrm{~g}=0$
$2 \mathrm{~g}(8 \mathrm{~g}+15)=0$
$g=0$ or $g=\frac{-15}{8}$
Hence equations of circles are
$\mathrm{x}^{2}+\mathrm{y}^{2}-1=0$ and $\mathrm{x}^{2}+\mathrm{y}^{2}-\frac{15}{4} \mathrm{x}-1=0$
$x^{2}+y^{2}-1=0$ and $4 x^{2}+4 y^{2}-15 x-4=0$
3. Prove that the two circles, which pass through $(0, a)$ and $(0,-a)$ and touch the line $y=m x+c$, will cut or thogonally if $\mathrm{c}^{2}=\mathrm{a}^{2}\left(2+\mathrm{m}^{2}\right)$
Show Answer
Solution:
Let the equation of the circles be
$x^{2}+y^{2}+2 g x+2 f y+d=0$
This circle passes through the points $(0, \mathrm{a})$ and $(0,-\mathrm{a})$
$\therefore \mathrm{a}^{2}+2 \mathrm{fa}+\mathrm{d}=0$
(1) and $\mathrm{a}^{2}-2 \mathrm{fa}+\mathrm{d}=0$
(1) (2)
$4 \mathrm{fa}=0$
$\therefore \mathrm{f}=0$ and $\mathrm{d}=-\mathrm{a}^{2}$
$\therefore$ The equation of circle is $\mathrm{x}^{2}+\mathrm{y}^{2}+2 \mathrm{gx}-\mathrm{a}^{2}=0$
Centre of this circle is $(-\mathrm{g}, 0)$ and radies $\sqrt{\mathrm{g}^{2}+\mathrm{a}^{2}}$
Since line $y=m x+c$ touches the circle
$\therefore\left|\frac{-\mathrm{mg}+\mathrm{c}}{\sqrt{\mathrm{m}^{2}+1}}\right|=\sqrt{\mathrm{g}^{2}+\mathrm{a}^{2}}$
$\mathrm{c}-\mathrm{mg}=\sqrt{\mathrm{g}^{2}+\mathrm{a}^{2}} \sqrt{\mathrm{m}^{2}+1}$
Squaring
$\mathrm{c}^{2}+\mathrm{m}^{2} \mathrm{~g}^{2}-2 \mathrm{mcg}=\mathrm{g}^{2} \mathrm{~m}^{2}+\mathrm{g}^{2}+\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{a}^{2}$
$\mathrm{g}^{2}+2 \mathrm{mcg}+\mathrm{a}^{2}\left(1+\mathrm{m}^{2}\right)-\mathrm{c}^{2}=0$
It is a quadratic in $\mathrm{g}$
$\therefore$ product of the roots $\mathrm{g} _{1} \mathrm{~g} _{2}=\mathrm{a}^{2}\left(1+\mathrm{m}^{2}\right)-\mathrm{c}^{2}$
Sum of roots $\mathrm{g} _{1}+\mathrm{g} _{2}=-2 \mathrm{mc}$
Now the equations of the two circles represented are $x^{2}+y^{2}+2 g _{1} x-a^{2}=0$ and $x^{2}+y^{2}+2 g _{2} x-a^{2}=$ 0
These two circles will be orthogonal if
$ \begin{aligned} & 2 \mathrm{~g} _{1} \mathrm{~g} _{2}=-\mathrm{a}^{2}-\mathrm{a}^{2} \\ & \mathrm{~g} _{1} \mathrm{~g} _{2}=-\mathrm{a}^{2} \end{aligned} $
But $\mathrm{g} _{1} \mathrm{~g} _{2}=-\mathrm{c}^{2}+\mathrm{a}^{2}\left(1+\mathrm{m}^{2}\right)$
$\therefore-\mathrm{c}^{2}+\mathrm{a}^{2}\left(1+\mathrm{m}^{2}\right)=-\mathrm{a}^{2}$
or $\mathrm{c}^{2}=\mathrm{a}^{2}\left(2+\mathrm{m}^{2}\right)$
Which is the required condition
4. If the angle of intersection of the circles $x^{2}+y^{2}+x+y=0$ and $x^{2}+y^{2}+x-y=0$ is $\theta$, then equation of the line passing through $(1,2)$ and making an angle $\theta$ with the $y$-axis is
Show Answer
Solution:
Let $C _{1}$ and $C _{2}$ be the centres of given circles $C _{1}\left(\frac{-1}{2}, \frac{-1}{2}\right)$ and $C _{2}\left(\frac{-1}{2}, \frac{1}{2}\right)$
Also radius these two circles are $r _{1}=\sqrt{\frac{1}{4}+\frac{1}{4}}=\sqrt{\frac{1}{2}}=\frac{1}{\sqrt{2}}$
and $\mathrm{r} _{2}=\sqrt{\frac{1}{4}+\frac{1}{4}}=\frac{1}{\sqrt{2}}$
$\cos \theta=\frac{\mathrm{r} _{1}{ }^{2}+\mathrm{r} _{2}{ }^{2}-\mathrm{d}^{2}}{2 \mathrm{r} _{1} \mathrm{r} _{2}}$
$=\frac{\frac{1}{2}+\frac{1}{2}-1}{2 \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}}$
$=0$
$\therefore \theta=\frac{\pi}{2}$
$\therefore$ Required line is parallel to $\mathrm{x}$-axis and it passes through $(1,2)$
$\therefore$ Equation of line is $\mathrm{y}=2$.
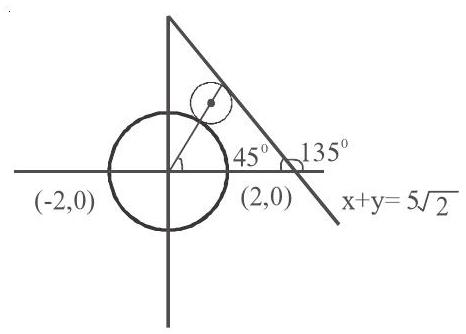
5. The equation of a circle is $x^{2}+y^{2}=4$. Find the centre of the smallest circle touching the circle and the line $x+y=5 \sqrt{2}$
Show Answer
Solution:
Here $\mathrm{OA}=2$ radius of circle $\mathrm{x}^{2}+\mathrm{y}^{2}=4$ with centre $(0,0)$
The distance of $(0,0)$ from $x+y=5 \sqrt{2}$ is
$\left|\frac{-5 \sqrt{2}}{\sqrt{2}}\right|=5$
$\therefore$ The radius of the smallest circle $=\frac{5-2}{2}=\frac{3}{2}$
and $\mathrm{OC}=2+\frac{3}{2}=\frac{7}{2}$
The slope of $\mathrm{OA}=1=\tan \theta$ $\therefore \cos \theta=\frac{1}{\sqrt{2}}$ and $\sin \theta=\frac{1}{\sqrt{2}}$
$\therefore$ Centre $(0+\mathrm{OC} \cos \theta, O+O C \sin \theta)=\left(\frac{7}{2 \sqrt{2}}, \frac{7}{2 \sqrt{2}}\right)$





