COMPLEX NUMBER - 5 (Loci in Complex plane)
1. Distance formula
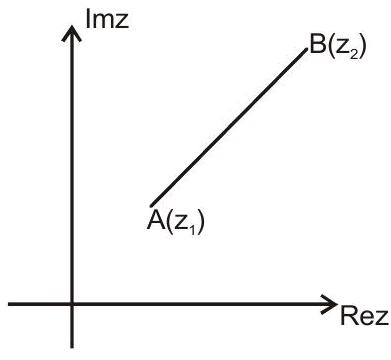
Distance between A & B
i.e. $\mathrm{AB}=\left|\mathrm{z} _{1}-\mathrm{z} _{2}\right|$
2. Section formula
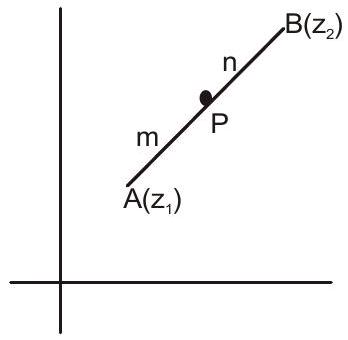
If $\mathrm{P}$ divides $\mathrm{AB}$ in the ratio
$m: n$ (internally), then $P$ is
$ \left(\frac{m z _{2}+n z _{1}}{m+n}\right) $
In case of external division, $\mathrm{P}$ is $\frac{\mathrm{mz} \mathrm{z} _{2}-\mathrm{nz}}{\mathrm{m}-\mathrm{n}}$.
If $\mathrm{P}$ is the mid point of $\mathrm{AB}$ then
$ \mathrm{P} \text { is }\left(\frac{\mathrm{z} _{1}+\mathrm{z} _{2}}{2}\right) $
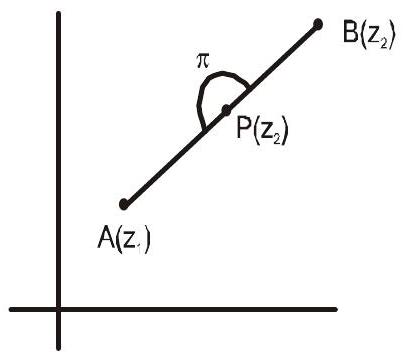
3. Straight line
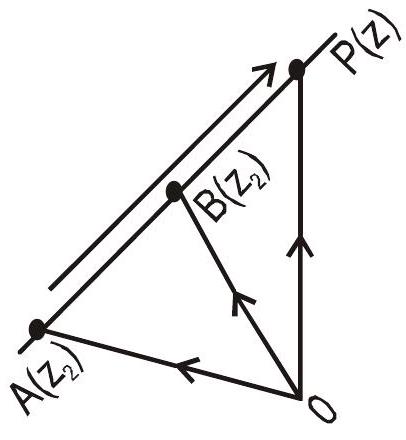
$\overline{\mathrm{OP}}=\overline{\mathrm{OA}}+\overline{\mathrm{AP}}$
i.e. $\overline{O P}=\overline{O A}+t \overline{A B}$
$t$ is some suitable real number
Now writing corresponding complex number, we get
$\mathrm{z}=\mathrm{z} _{1}+\mathrm{t}\left(\mathrm{z} _{2}-\mathrm{z} _{1}\right)……..(1)$
Since Value of $t$ is different for different position of $\mathrm{P}$.
$\therefore t$ is called a parameter & the equation (1) is called the parametric equation of straight line passing through the fixed points $\mathrm{A}\left(\mathrm{z} _{1}\right) \& \mathrm{~B}\left(\mathrm{z} _{2}\right)$.
Cartesian equation of (1) Put $z=x+i y, z _{1}=x _{1}+i y _{1} \& z _{2}=x _{2}+i y _{2}$ in (1)
If we get $x+i y=x _{1}+i y _{1}+t\left(\left(x _{2}-x _{1}\right)+\left(y _{2}-y _{1}\right)\right)$
$\mathrm{x}=\mathrm{x} _{1}+\mathrm{t}\left(\mathrm{x} _{2}-\mathrm{x} _{1}\right) \& \mathrm{y}=\mathrm{y} _{1}+\mathrm{t}\left(\mathrm{y} _{2}-\mathrm{y} _{1}\right)$
or $\frac{\mathrm{x}-\mathrm{x} _{1}}{\mathrm{x} _{2}-\mathrm{x} _{1}}=\frac{\mathrm{y}-\mathrm{y} _{1}}{\mathrm{y} _{2}-\mathrm{y} _{1}}=\mathrm{t}$
From (1) $\frac{z-z _{1}}{z _{2}-z _{1}}=t$
$\because \mathrm{t}$ is Purely real number.
so, $\operatorname{Im}\left(\frac{z-z_1}{z_2-z_1}\right)=0………..(2)$
( $\mathrm{z}=\overline{\mathrm{z}} _{1}$, then $\mathrm{z}$ is purely real)
$\Rightarrow \frac{z-z _{1}}{z _{2}-z _{1}}=\left(\overline{z-z _{1}}\right)$
$\Rightarrow \frac{\mathrm{z}-\mathrm{z} _{1}}{\mathrm{z} _{2}-\mathrm{z} _{1}}=\frac{\overline{\mathrm{z}}-\overline{\mathrm{z}} _{1}}{\overline{\mathrm{z}} _{2}-\overline{\mathrm{z}} _{1}}$
$\Rightarrow \quad \mathrm{z} \overline{\mathrm{z}} _{2}-\mathrm{z} \overline{\mathrm{z}} _{1}-\mathrm{z} _{1} \overline{\mathrm{z}} _{2}+\mathrm{z} _{1} \overline{\mathrm{z}} _{1}=\overline{\mathrm{z}} \mathrm{z} _{2}-\overline{\mathrm{z}} _{1} \mathrm{z} _{2}-\mathrm{z} _{1} \overline{\mathrm{z}}+\mathrm{z} _{1} \overline{\mathrm{z}} _{1}$
$\Rightarrow\left|\begin{array}{lll}1 & 1 & 1 \\ \mathrm{z} & \mathrm{z} _{1} & \mathrm{z} _{2} \\ \overline{\mathrm{z}} & \bar{z} _{1} & \bar{z} _{2}\end{array}\right|=0 \Rightarrow\left|\begin{array}{ccc}\mathrm{z} & \overline{\mathrm{z}} & 1 \\ \mathrm{z} _{1} & \bar{z} _{1} & 1 \\ \mathrm{z} _{2} & \bar{z} _{2} & 1\end{array}\right|=0………(3)$
Slope of this line is $\frac{z _{1}-z _{2}}{\bar{z} _{1}-\bar{z} _{2}}$.
Since, $z\left(\bar{z} _{1}-\bar{z} _{2}\right)-\bar{z}\left(z _{1}-z _{2}\right)+z _{1} \cdot \bar{z} _{2}-\bar{z} _{1} \cdot z _{2}=0$
$\Rightarrow \quad \mathrm{i}\left(\overline{\mathrm{z}} _{1}-\overline{\mathrm{z}} _{2}\right) \mathrm{z}-\mathrm{i}\left(\mathrm{z} _{1}-\mathrm{z} _{2}\right) \overline{\mathrm{z}}+\mathrm{i}\left(\mathrm{z} _{1} \cdot \overline{\mathrm{z}} _{2}-\overline{\mathrm{z}} _{1} \cdot \mathrm{z} _{2}\right)=0$
$\Rightarrow \quad \overline{\mathrm{a}} \mathrm{z}+\mathrm{a} \overline{\mathrm{z}}+\mathrm{b}=0………(4)$
where $\mathrm{b}=\mathrm{i}\left(\mathrm{z} _{1} \overline{\mathrm{z}} _{2}-\overline{\mathrm{z}} _{1} \cdot \mathrm{z} _{2}\right)$
$ \begin{aligned} & =i\left(z _{1} \bar{z} _{2}-\overline{\bar{z} _{1} \cdot z _{2}}\right) \\ & =i \cdot 2 \mathrm{i} \operatorname{Im}\left(\mathrm{z} _{1} \bar{z} _{2}\right) \\ & =-2 \operatorname{Im}\left(\mathrm{z} _{1} \overline{\mathrm{z}} _{2}\right)=\text { a real number } \& \mathrm{a} \neq 0 \text { as }\left(\mathrm{z} _{1} \neq \mathrm{z} _{2}\right) \end{aligned} $
-
Points $\mathrm{z} _{1}, \mathrm{z} _{2}, \mathrm{z} _{3}$ are collinear if and only if $\left|\begin{array}{lll}\mathrm{z} _{1} & \overline{\mathrm{z}} _{1} & 1 \\ \mathrm{z} _{2} & \overline{\mathrm{z}} _{2} & 1 \\ \mathrm{z} _{3} & \overline{\mathrm{z}} _{3} & 1\end{array}\right|=0$
-
Equation (2) & (3) represent the non parametric form of equation of straight line passing through the point $\mathrm{A}\left(\mathrm{z} _{1}\right) \& \mathrm{~B}\left(\mathrm{z} _{2}\right)$
-
Equation (4) is called general equation with slope $\left(\frac{-a}{\bar{a}}\right)=-\left(\frac{a}{\bar{a}}\right)$
4. Equation of Perpendicular Bisector
We consider two fixed points $\mathrm{A}\left(\mathrm{z} _{1}\right)$ & $\mathrm{B}\left(\mathrm{z} _{2}\right)$ and variable point $\mathrm{P}(\mathrm{z})$ moving such that $\mathrm{AP}=\mathrm{BP}$
i.e. $\left|z-z _{1}\right|=\left|z-z _{2}\right|…….(5)$
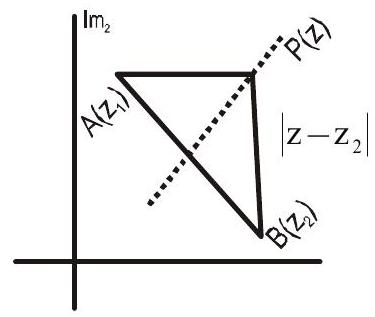
From Geometry, it is obvious that $\mathrm{P}$ lies on the perpendicular bisector of the segment $\mathrm{AB}$.
$\therefore \quad$ Equaiton (5) is the equation of perpendicular bisector of the segment joining $\mathrm{A}\left(\mathrm{z} _{1}\right) \& \mathrm{~B}\left(\mathrm{z} _{2}\right)$.
5. Another form of perpendicular bisector
$\left|z-z _{1}\right|=\left|z-z _{2}\right| \Rightarrow\left|z-z _{1}\right|^{2}=\left|z-z _{2}\right|^{2} \Rightarrow\left(z-z _{1}\right)\left(\bar{z}-\overline{z _{1}}\right)=\left(z-z _{2}\right)\left(\bar{z}-\overline{z _{2}}\right)$
- If $\mathrm{A}\left(\mathrm{z} _{1}\right)$ and $\mathrm{B}\left(\mathrm{z} _{2}\right)$ are two fixed points and $\mathrm{P}$ is a variable moving on the line segment $\mathrm{AB}$ then $\mathrm{AP}+\mathrm{BP}=\mathrm{AB}$
i.e. $\left|z-z _{1}\right|+\left|z-z _{2}\right|=\left|z _{1}-z _{2}\right|………(6)$
$\therefore \quad$ above equation represents the line segment $\mathrm{AB}$

i.e. $\quad\left|z-z _{1}\right|-\left|z-z _{2}\right|=\left|z _{1}-z _{1}\right|……….(7)$
i.e. $\left|z-z _{1}\right|-\left|z-z _{2}\right|=-\left|z _{1}-z _{1}\right|………..(8)$
From equation (7) & (8), it is clear that $p$ is lying on the line passing through $A \& B$ but not lying on the segment $\mathrm{AB}$.
If $z _{1}$ and $z _{2}$ are two unequal complex numbers represented by points $P$ and $Q$,
then $\frac{z _{1}-z _{2}}{\bar{z} _{1}-\bar{z} _{2}}$ is called the complex slope of the line joining $z _{1} \& z _{2}$.
Thus $\mathrm{w}=\frac{\mathrm{z} _{1}-\mathrm{z} _{2}}{\overline{\mathrm{Z}} _{1}-\overline{\mathrm{Z}} _{2}}$
then $|w|=\frac{\left|z _{1}-z _{2}\right|}{\left|\bar{z} _{1}-\bar{z} _{2}\right|}=\frac{\left|z _{1}-z _{2}\right|}{\left|z _{1}-z _{2}\right|}=1$
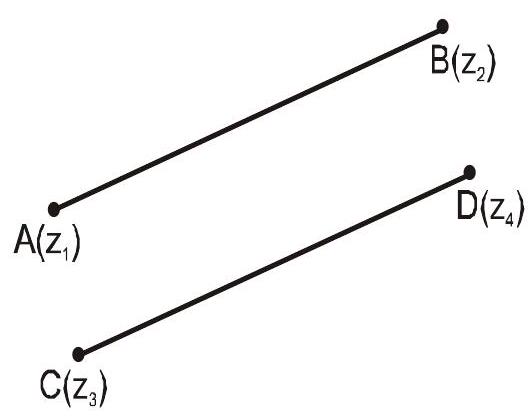
- Two lines having complex slopes $\mathrm{w} _{1}$ and $\mathrm{w} _{2}$ are parallel if and only if $\mathrm{w} _{1}=\mathrm{w} _{2}$
$\mathrm{w} _{1}=\frac{\mathrm{Z} _{1}-\mathrm{Z} _{2}}{\overline{\mathrm{Z}} _{1}-\overline{\mathrm{Z}} _{2}}$ (complex slope of $\left.\mathrm{AB}\right)$
$\mathrm{w} _{2}=\frac{\mathrm{z} _{3}-\mathrm{z} _{4}}{\overline{\mathrm{z}} _{3}-\overline{\mathrm{z}} _{4}}$ (complex slope of CD)
$\mathrm{AB} | \mathrm{CD} \Rightarrow$ angle $\mathrm{b} / \mathrm{w} \mathrm{AB}$ and $\mathrm{CD}=0$ or $\pi$
$\Rightarrow \quad \operatorname{argument}\left(\frac{z _{2}-z _{1}}{z _{4}-z _{3}}\right)=0$ or $\pi$
$\Rightarrow\left(\frac{z _{2}-z _{1}}{z _{4}-z _{3}}\right)$ is real
$\Rightarrow\left(\overline{\frac{\mathrm{z}_2-\mathrm{z}_1}{\mathrm{z}_4-\mathrm{z}_3}}\right)=\frac{\mathrm{z}_2-\mathrm{z}_1}{\mathrm{z}_4-\mathrm{z}_3} \Rightarrow\left(\overline{\frac{\mathrm{z}_1-\mathrm{z}_2}{\mathrm{z}_3-\mathrm{z}_4}}\right)=\frac{\mathrm{z}_1-\mathrm{z}_2}{\mathrm{z}_3-\mathrm{z}_4}$
$\Rightarrow \quad \frac{\mathrm{z} _{1}-\mathrm{z} _{2}}{\overline{\mathrm{z}} _{1}-\overline{\mathrm{z}} _{2}}=\frac{\mathrm{z} _{3}-\mathrm{z} _{4}}{\overline{\mathrm{z}} _{3}-\overline{\mathrm{z}} _{4}} \Rightarrow \mathrm{w} _{1}=\mathrm{w} _{2}$
-
The two lines having complex slope $\mathrm{w} _{1} \& \mathrm{w} _{2}$ are perpendicular if and only if $\mathrm{w} _{1}=-\mathrm{w} _{2}$.
-
The equation of a line parallel to $a \bar{z}+\bar{a} z+b=0$ is $\mathrm{a} \overline{\mathrm{z}}+\overline{\mathrm{a}} \mathrm{z}+\lambda=0$, where $\lambda \in R^{\prime}$
-
The equation of a line perpendicular to the line $a \bar{z}+\bar{a} z+b=0$ is $\mathrm{a} \overline{\mathrm{z}}-\overline{\mathrm{a}} \mathrm{z}+\lambda=0$, where $\lambda \in R^{\prime \prime}$
-
The length of perpendicular from a point $\mathrm{P}\left(\mathrm{z} _{0}\right)$ to the line $\mathrm{a} \overline{\mathrm{z}}+\overline{\mathrm{a}} \mathrm{z}+\mathrm{b}=0$ is $\left|\frac{\mathrm{a} \bar{z} _{0}+\overline{\mathrm{a}} _{0}+\mathrm{b}}{2|\mathrm{a}|}\right|$.
CIRCLE
Consider a fixed point $\mathrm{c}\left(\mathrm{z} _{0}\right)$ and a variable point $\mathrm{P}(\mathrm{z})$ which is moving, keeping its distance from the point $\mathrm{C}$ a constant $\mathrm{R}$
$\therefore \quad$ At any position, $\mathrm{P}(\mathrm{z})$ satisfies the equation $\left|z-z _{0}\right|=R$
Equation(1) represents the points on a circle whose centre is $\mathrm{c}\left(\mathrm{z} _{0}\right)$ & radius is $\mathrm{R}$.
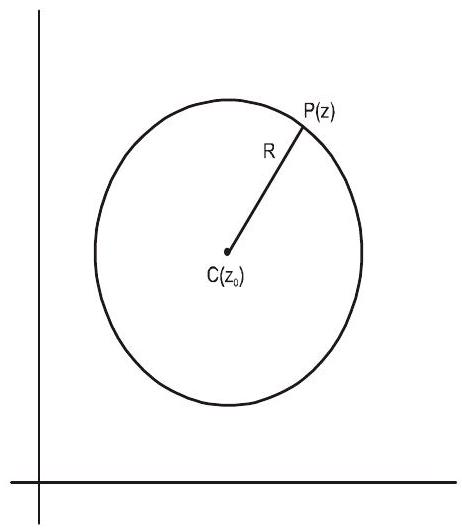
Cartesian form
$\left|z-z _{0}\right|^{2}=R^{2}$.
Let $\mathrm{z}=\mathrm{x}+\mathrm{iy} \& \mathrm{z} _{0}=\mathrm{x} _{0}+\mathrm{iy} _{0}$
$\left|\left(x-x _{0}\right)+i\left(y-y _{0}\right)\right|^{2}=R^{2}$
$\left(\mathrm{x}-\mathrm{x} _{0}\right)^{2}+\left(\mathrm{y}-\mathrm{y} _{0}\right)^{2}=\mathrm{R}^{2}$
General equation of a circle
$\bar{z} z+\bar{a} z+a \bar{z}+b=0$ where $b$ is real. The centre of this circle is - a and radius is $\sqrt{\mathrm{a} \overline{\mathrm{a}}-\mathrm{b}}=\sqrt{|\mathrm{a}|^{2}-\mathrm{b}}$
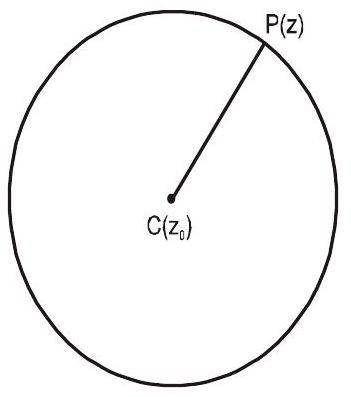
Explanation: Let $z _{0}$ be the centre of the circle and $\mathrm{P}(\mathrm{z})$ be any point on the circle.
Then $\left|z-z _{0}\right|=r$ or $\left|z-z _{0}\right|^{2}=r^{2}$
$\Rightarrow \quad\left(\mathrm{z}-\mathrm{z} _{0}\right)\left(\overline{\mathrm{z}-\mathrm{z} _{0}}\right)=\mathrm{r}^{2} \Rightarrow\left(\mathrm{z}-\mathrm{z} _{0}\right)\left(\overline{\mathrm{z}}-\overline{\mathrm{z}} _{0}\right)=\mathrm{r}^{2}$
$\Rightarrow \quad \mathrm{z} \overline{\mathrm{z}}-\overline{\mathrm{z}} _{0} \mathrm{z}-\mathrm{z} _{0} \overline{\mathrm{z}}+\left|\mathrm{z} _{0}\right|^{2}-\mathrm{r}^{2}=0$
$\Rightarrow \quad \mathrm{z} \overline{\mathrm{z}}-\overline{\mathrm{a}} \mathrm{z}+\mathrm{a} \overline{\mathrm{z}}+\mathrm{b}=0$
Where $\mathrm{a}=-\mathrm{z} _{0}, \mathrm{~b}=\left|\mathrm{z} _{0}\right|^{2}-\mathrm{r}^{2}=0$ real number clearly centre of the circle (1) is $\mathrm{z} _{0}$ i.e. $-\mathrm{a} \& $ radius $=\sqrt{\left|z _{0}\right|^{2}-b}=\sqrt{|a|^{2}-b}$
- Equation of the circle whose one diameter is the line segment joining $z _{1} \& z _{2}$ is
$\frac{\mathrm{z}-\mathrm{z} _{1}}{\mathrm{Z}-\mathrm{z} _{2}}+\frac{\overline{\mathrm{z}}-\overline{\mathrm{z}} _{1}}{\overline{\mathrm{z}}-\overline{\mathrm{Z}} _{2}}=0$
$\because \quad \angle \mathrm{APB}=\frac{\pi}{2}$
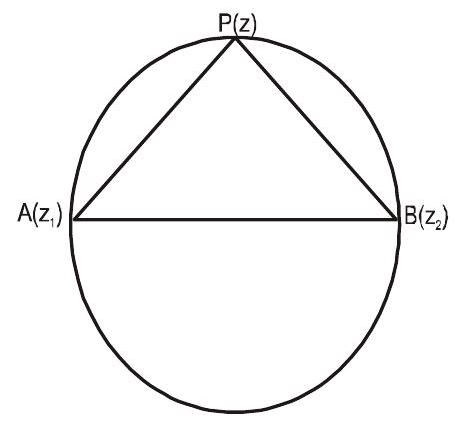
argument $\left(\frac{\mathrm{z} _{2}-\mathrm{z}}{\mathrm{z} _{1}-\mathrm{z}}\right)=\frac{\pi}{2} \Rightarrow \frac{\mathrm{z} _{2}-\mathrm{z}}{\mathrm{z} _{1}-\mathrm{z}}$ is purely imaginary
or $\left(\frac{\overline{z _{2}-z}}{\overline{z _{1}-z}}\right)=-\left(\frac{z _{2}-z}{z _{1}-z}\right)$
$\Rightarrow \frac{\overline{\mathrm{z}} _{2}-\overline{\mathrm{z}}}{\overline{\mathrm{z}} _{1}-\overline{\mathrm{z}}}=-\frac{\left(\mathrm{z} _{2}-\mathrm{z}\right)}{\mathrm{z} _{1}-\mathrm{z}} \Rightarrow \frac{\overline{\mathrm{z}} _{1}-\overline{\mathrm{z}}}{\overline{\mathrm{z}} _{2}-\overline{\mathrm{z}}}=-\frac{\mathrm{z} _{2}-\mathrm{z}}{\mathrm{z} _{1}-\mathrm{z}}$
$\Rightarrow \quad \frac{\bar{z}-\bar{z} _{2}}{\bar{z}-\bar{z} _{1}}=-\frac{\mathrm{z}-\mathrm{z} _{2}}{\mathrm{z}-\mathrm{z} _{1}}$ or $\frac{\mathrm{z}-\mathrm{z} _{1}}{\mathrm{z}-\mathrm{z} _{2}}+\frac{\overline{\mathrm{z}}-\overline{\mathrm{z}} _{1}}{\overline{\mathrm{z}}-\overline{\mathrm{z}} _{2}}=0$
$\Rightarrow \quad\left(\mathrm{z}-\mathrm{z} _{1}\right)\left(\overline{\mathrm{z}}-\overline{\mathrm{z}} _{2}\right)+\left(\mathrm{z}-\mathrm{z} _{2}\right)\left(\overline{\mathrm{z}}-\overline{\mathrm{z}} _{1}\right)=0$
- $\quad\left|\mathrm{z}-\mathrm{z} _{1}\right|=\mathrm{k}\left|\mathrm{z}-\mathrm{z} _{2}\right| \Rightarrow \mathrm{AP}=\mathrm{KBA} \Rightarrow$ Locus of $\mathrm{P}(\mathrm{z})$ is a circle $(\mathrm{k} \neq 1)$
- $\quad\left|\mathrm{z}-\mathrm{z} _{1}\right|+\left|\mathrm{z}-\mathrm{z} _{2}\right|=\mathrm{k}\left(\neq\left|\mathrm{z} _{1}-\mathrm{z} _{2}\right|\right) \Rightarrow \mathrm{PA}+\mathrm{PB}=\mathrm{k}$ be locus of $\mathrm{z}$ is an ellipse where $\mathrm{A} \& \mathrm{~B}$ are foci of the ellipse.
- $\quad\left|\mathrm{z}-\mathrm{z} _{1}\right|-\left|\mathrm{z}-\mathrm{z} _{2}\right|=\mathrm{k}\left(\neq\left|\mathrm{z} _{1}-\mathrm{z} _{2}\right|\right) \Rightarrow \mathrm{PA}-\mathrm{PB}=\mathrm{k}$ be locus of $\mathrm{z}$ is an ellipse where $\mathrm{A} \& \mathrm{~B}$ are foci at $\mathrm{A} \& \mathrm{~B}$.
- $\quad\left|z-z _{1}\right|^{2}+\left|z-z _{2}\right|^{2}=\left|z _{1}-z _{2}\right|^{2}$, locus of $z$ is a circle.
- $\quad \operatorname{argument}\left(\frac{z-z _{1}}{z-z _{2}}\right)=\alpha _{\text {(fixed), locus of } z \text { is segment of a circle. }}$
- $\quad$ argument $\left(\frac{z-z _{1}}{z-z _{2}}\right)= \pm \frac{\pi}{2}$, locus of $\mathrm{z}$ is a circle with $\mathrm{z} _{1}$ and $\mathrm{z} _{2}$ as the vertices of diameter.
- $\quad \operatorname{argument}\left(\frac{z-z _{1}}{z-z _{2}}\right)=0$ or $\pi$, locus of $\mathrm{z}$ is a straight line passing through $\mathrm{z} _{1} \& \mathrm{z} _{2}$.
Practice questions
1. If $\mathrm{Z}=\mathrm{x}+\mathrm{iy}$ and $\omega=\frac{1-i z}{z-i}$, then $|\omega|=1$ implies that, in the complex plane
(a). $z$ lies on the imaginary axis
(c). $z$ lies on the unit circle
(b). $ \mathrm{z}$ lies on the real axis
(d). none of these
Show Answer
Answer: (b)2. The points $\mathrm{z} _{1}, \mathrm{z} _{2}, \mathrm{z} _{3}, \mathrm{z} _{4}$ in the complex plane are the vertices of a parallelogram taken in order if and only if
(a). $\mathrm{z} _{1}+\mathrm{z} _{4}=\mathrm{z} _{2}+\mathrm{z} _{3}$
(b). $\mathrm{z} _{1}+\mathrm{z} _{3}=\mathrm{z} _{2}+\mathrm{z} _{4}$
(c). $\mathrm{z} _{1}+\mathrm{z} _{2}=\mathrm{z} _{3}+\mathrm{z} _{4}$
(d). none of these
Show Answer
Answer: (b)3. For all complex numbers $\mathrm{z} _{1}, \mathrm{z} _{2}$ satisfying $\left|z _{1}\right|=12$ and $\left|z _{2}-3-4 i\right|=5$, the minimum value of $\left|z _{1}-z _{2}\right|$ is
(a). $0$
(b). $2$
(c). $7$
(d). $17$
Show Answer
Answer: (b)4. If $|z|=1$, then the point representing the complex number $-1+3 z$ will lie on
(a). a circle
(b). a straight line
(c). a parabola
(d). a hyperbola
Show Answer
Answer: (a)5. If $\mathrm{z}=(\lambda+3)-i \sqrt{5-\lambda^{2}}$, then the locus of $\mathrm{z}$ is
(a). ellipse
(b). semicircle
(c). parabola
(d). straight line
Show Answer
Answer: (b)6. If $z$ is complex number then the locus of $z$ satisfying the condition $|2 z-1|=|z-1|$ is
(a). perpendicular bisector of line segment joining $1 / 2$ and 1
(b). circle
(c). parabola
(d). none of the above curves
Show Answer
Answer: (b)7. If $\operatorname{Im}\left(\frac{2 z+1}{i z+1}\right)=-2$ then the locus of the point representing $\mathrm{z}$ in the complex plane is
(a). circle
(b). a straight line
(c). a parabola
(d). none of these
Show Answer
Answer: (b)8. If $\left|z _{1}\right|=\left|z _{2}\right|=\left|z _{3}\right|=\left|z _{4}\right|$ then the points representing $\mathrm{z} _{1}, \mathrm{z} _{2}, \mathrm{z} _{3}, \mathrm{z} _{4}$ are
(a). concyclic
(c). vertices of a rhombus
(b). vertices of a square
(d). none of these
Show Answer
Answer: (a)9. The equation $z \bar{z}+(4-3 i) z+(4+3 i) \bar{z}+5=0$ represents a circle whose radius is
(a). $5$
(b). $2 \sqrt{5}$
(c). $\frac{5}{2}$
(d). none of these
Show Answer
Answer: (a)10. The equation $|\mathrm{z}-\mathrm{i}|+|\mathrm{z}+\mathrm{i}|=\mathrm{k}, \mathrm{k}>0$, can represent an ellipse if $\mathrm{k}^{2}$ is
(a). $<1$
(b). $<2$
(c). $>4$
(d). none of these
Show Answer
Answer: (c)11. The equation $|z+i|-|z-i|=k$ represents hyperbola if
(a). $-2<k<2$
(b). $k>2$
(c). $0<\mathrm{k}<2$
(d). none of these
Show Answer
Answer: (a)12. Let $z=1-t+i \sqrt{t^{2}+t+2}$, where $t$ is a parameter. The locus of $\mathrm{z}$ in the Argand plane is
(a). a hyperbola
(b). an ellipse
(c). a straight line
(d). None of these
Show Answer
Answer: (a)13. Let $z _{1}$ and $z _{2}$ be two non-real complex cube roots of unity and $\left|z-z _{1}\right|^{2}+\left|z-z _{2}\right|^{2}=\lambda$ be the equation of a circle with $z _{1}, z _{2}$ as ends of a diameter, then the value of $\lambda$ is
(a). $4$
(b). $3$
(c). $2$
(d). $\sqrt{2}$
Show Answer
Answer: (b)14. If the equation $\left|z-z _{1}\right|^{2}+\left|z-z _{2}\right|^{2}=k$ represents the equation of a circle, where $\mathrm{z} _{1}=2+3 \mathrm{i}$, $z _{2}=4+3 \mathrm{i}$ are the extremities of a diameter, then the value of $k$ is
(a). $1 / 4$
(b). $4$
(c). $2$
(d). none of these
Show Answer
Answer: (b)15. Let $\alpha$ and $\beta$ be two fixed non-zero complex numbers and $z$ a variable complex number. If the lines $\alpha \bar{z}+\bar{\alpha} z+1$ and $\bar{\beta} \bar{z}+\bar{\beta} z-1=0$ are mutually perpendicular, then
(a). $\alpha \beta+\bar{\alpha} \bar{\beta}=0$
(b). $\alpha \beta-\bar{\alpha} \bar{\beta}=0$
(c). $\bar{\alpha} \beta-\alpha \bar{\beta}=0$
(d). $\alpha \bar{\beta}+\bar{\alpha} \beta=0$





