ELLIPSE-3
Topics covered
1. Auxilliary circle
2. Eccentric angle
3. Equation of chord
4. Position of a point with respect to an ellipse.
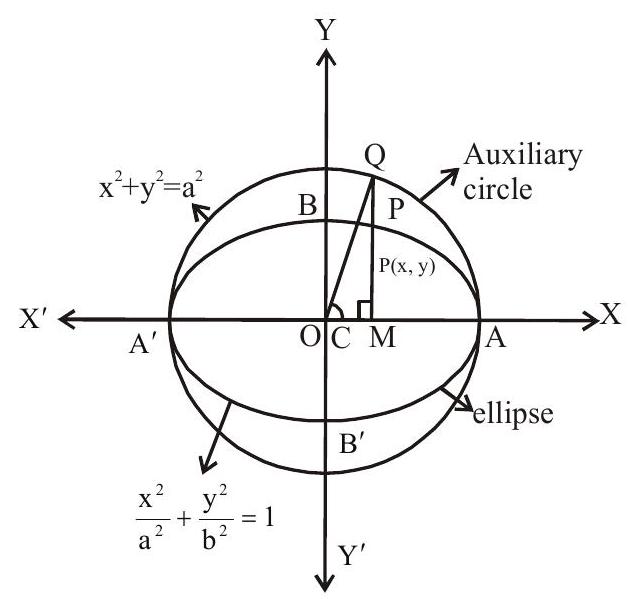
1. Auxiliary Circle
The circle described on the major axis of an ellipse as diameter is called an auxiliary circle of the ellipse
If $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ is an ellipse then its auxiliary circle is $x^{2}+y^{2}=a^{2}$
2. Eccentric angle of a point
Let $\mathrm{P}$ be any point on the ellipse $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$
Draw PM perpendicular to major axis from $\mathrm{P}$ and produce MP to meet the auxiliary circle at Q. Join CQ. $\angle \mathrm{QCA}=\theta$ is called eccentric angle of point $\mathrm{P}$ Note that the angle ACP is not eccentric angle. i.e. eccentric angle of $\mathrm{P}$ on an ellipse is the angle which the radius through the corresponding point on, the auxiliary circle makes with the major axis
$\therefore \mathrm{Q}(\operatorname{acos} \theta, \operatorname{asin} \theta)$
$\therefore \mathrm{x}$-coordinate of $\mathrm{P}$ is acos $\theta$
$\frac{\mathrm{a}^{2} \cos ^{2} \theta}{\mathrm{a}^{2}}+\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$
$\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1-\cos ^{2} \theta$
$\mathrm{y}^{2} \quad=\mathrm{b}^{2} \sin ^{2} \theta$
$\mathrm{y}=\mathrm{b} \sin \theta$
$\therefore$ Coordinate of $\mathrm{P}$ is $(\operatorname{acos} \theta, \mathrm{bsin} \theta)$
i.e. $x=a \cos \theta$ and $y=b \sin \theta$ is the parameter equations of the ellipse.
$(a \cos \theta, b \sin \theta)$ is also called the point ’ $\theta$ '
3. Equation of the chord
$\operatorname{Let} \mathrm{P}(\operatorname{acos} \theta, b \sin \theta)$ and $\mathrm{Q}(\operatorname{acos} \phi, \mathrm{bsin} \phi)$ be any two points of the ellipse $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ then the equation of the chord joining these two points is
$y-b \sin \theta=\frac{b \sin \phi-b \sin \theta}{a \cos \phi-a \cos \theta}(x-a \cos \theta)$
Simplifying the equation we get
$\frac{\mathrm{x}}{\mathrm{a}} \cos \left(\frac{\theta+\phi}{2}\right)+\frac{\mathrm{y}}{\mathrm{b}} \sin \left(\frac{\theta+\phi}{2}\right)=\cos \frac{\theta-\phi}{2}$
$\theta \& \phi$ are eccentric angle of points $\mathrm{P}$ and $\mathrm{Q}$ of ellipse
4. Position of a point $(\mathrm{h}, \mathrm{k})$ with respect to an ellipse
Let ellipse be $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$
Now P will lie outside, on or inside the ellipse $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ according as
$\frac{\mathrm{h}^{2}}{\mathrm{a}^{2}}+\frac{\mathrm{k}^{2}}{\mathrm{~b}^{2}}-1>,=,<0$
Examples
1. Find the equation of the curve whose parametric equation are $x=1+4 \cos \theta, y=2+3 \sin \theta \in \mathrm{R}$
Show Answer
Solution: We have $x =1+4 \cos \theta, y=2+3 \sin \theta$
$ \therefore \frac{\mathrm{x}-1}{4}=\cos \theta \text { and } \frac{\mathrm{y}-2}{3}=\sin \theta $
Squaring and adding we get
$ \begin{aligned} & \left(\frac{x-1}{4}\right)^{2}+\left(\frac{y-2}{3}\right)^{2}=\cos ^{2} \theta+\sin ^{2} \theta \\ & \frac{(x-1)^{2}}{16}+\frac{(y-2)^{2}}{9}=1 \end{aligned} $
Which is an ellipse.
2. Find the eccentric angle of a point on the ellipse $\frac{x^{2}}{6}+\frac{y^{2}}{2}=1$ whose distance from the centre of the ellipse is $\sqrt{5}$
Show Answer
Solution :
We have $\frac{\mathrm{x}^{2}}{6}+\frac{\mathrm{y}^{2}}{2}=1$
$ \begin{array}{ll} a^{2}=6 & b^{2}=2 \\ a=\sqrt{6} & b=\sqrt{2} \end{array} $
$\therefore$ any point on the ellipse with $\theta$ as eccentric angle is $\mathrm{P}(\sqrt{6} \cos \theta, \sqrt{2} \sin \theta)$
Here centre is origin
$ \begin{aligned} \therefore C P= & \sqrt{6 \cos ^{2} \theta+2 \sin ^{2} \theta}=\sqrt{5} \\ \Rightarrow & 6 \cos ^{2} \theta+2 \sin ^{2} \theta=5 \\ \Rightarrow & 4 \cos ^{2} \theta=3 \\ & \cos ^{2} \theta=\frac{3}{4} \\ & \cos \theta= \pm \frac{\sqrt{3}}{2} \\ \therefore & \theta=\frac{\pi}{6}, \frac{5 \pi}{6}, \frac{7 \pi}{6}, \frac{11 \pi}{6} \end{aligned} $
3. If $\alpha$ and $\beta$ are the eccentric angles of the extremities of a focal chord of an ellipse, then the eccentricity of the ellipse is
(a) $\frac{\cos \alpha+\cos \beta}{\cos (\alpha-\beta)}$
(b) $\frac{\sin \alpha-\sin \beta}{\sin (\alpha-\beta)}$
(c) $\frac{\cos \alpha-\cos \beta}{\cos (\alpha-\beta)}$
(d) $\frac{\sin \alpha+\sin \beta}{\sin (\alpha+\beta)}$
Show Answer
Solution : Equation of chord joining points having eccentric angles $\alpha$ and $\beta$ is
$ \frac{x}{a} \cos \left(\frac{\alpha+\beta}{2}\right)+\frac{y}{b} \sin \left(\frac{\alpha+\beta}{2}\right)=\cos \left(\frac{\alpha-\beta}{2}\right) $
Since these points are extremities of focal chord so it passes through focus (ae, 0 ) then
$\therefore \mathrm{e} \cos \left(\frac{\alpha+\beta}{2}\right)=\cos \left(\frac{\alpha-\beta}{2}\right)$
$e=\frac{\cos \left(\frac{\alpha-\beta}{2}\right)}{\cos \left(\frac{\alpha+\beta}{2}\right)}$
Multiply & divide by $2 \sin \left(\frac{\alpha+\beta}{2}\right)$ on right side
$e=\frac{2 \sin \left(\frac{\alpha+\beta}{2}\right) \cos \left(\frac{\alpha-\beta}{2}\right)}{2 \sin \left(\frac{\alpha+\beta}{2}\right) \cos \left(\frac{\alpha+\beta}{2}\right)}$
$\mathrm{e}=\frac{\sin \alpha+\sin \beta}{\sin (\alpha+\beta)}$
4. An ellipse passes through the point $(4,-1)$ and touches the line $x+4 y-10=0$. Find its equation of its axes coincide with coordinate axes.
Show Answer
Solution : Let the equation of ellipse be $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$
It passes through $(4,-1)$
$ \therefore \frac{16}{\mathrm{a}^{2}}+\frac{1}{\mathrm{~b}^{2}}=1 \text { or } \mathrm{a}^{2}+16 \mathrm{~b}^{2}=\mathrm{a}^{2} \mathrm{~b}^{2} ………(1) $
$\mathrm{x}+4 \mathrm{y}-10=0$ is a tangent to the ellipse.
$y=-\frac{1}{4} x+\frac{10}{4} \Rightarrow y=m x+c$
$\mathrm{m}=-\frac{1}{4}, \mathrm{c}=\frac{10}{4}$
$c=\sqrt{a^{2} m^{2}+b^{2}}$ is a condition for tangent
$\frac{10}{4}=\sqrt{\mathrm{a}^{2} \times \frac{1}{16}+\mathrm{b}^{2}}$
$\frac{100}{16}=\frac{\mathrm{a}^{2}}{16}+\mathrm{b}^{2}$
$16 b^{2}=100-a^{2}$
$a^{2}+16 b^{2}=100$
From (1) we get
$100=\mathrm{a}^{2} \mathrm{~b}^{2}$
$\mathrm{b}^{2}=\frac{100}{\mathrm{a}^{2}}$
$\mathrm{a}^{2}+\frac{1600}{\mathrm{a}^{2}}=100$
$\mathrm{a}^{4}-100 \mathrm{a}^{2}+1600=0$
$\mathrm{a}^{4}-80 \mathrm{a}^{2}-20 \mathrm{a}^{2}+1600=0$
$\mathrm{a}^{2}\left(\mathrm{a}^{2}-80\right)-20\left(\mathrm{a}^{2}-80\right)=0$
$\left(a^{2}-80\right)\left(a^{2}-20\right)=0$
$\mathrm{b}^{2}=\frac{10}{8}=\frac{5}{4}$ or $\mathrm{b}^{2} \frac{100}{20}=5$
$\therefore$ Equation of ellipse is $\frac{\mathrm{x}^{2}}{80}+\frac{4 \mathrm{y}^{2}}{5}=1$
$ \text { or } \quad \frac{x^{2}}{20}+\frac{y^{2}}{5}=1 $
5. If $\frac{x}{a}+\frac{y}{b}=\sqrt{2}$ touches the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$, then find its eccentric angle $\theta$ of point of contact.
Show Answer
Solution : Let $\theta$ be the eccentric angle of the point of contact :
$\therefore$ coordinates of the point is $(a \cos \theta, b \sin \theta)$
Equation of tangent at this point is
$\frac{x \cos \theta}{a}+\frac{y \sin \theta}{b}-1=0 …….(1)$
Given that $\frac{\mathrm{x}}{\mathrm{a}}+\frac{\mathrm{y}}{\mathrm{b}}-\sqrt{2}=0………(2)$ is tangent
Comparing (1) and (2) as these two are identical, we get
$ \begin{aligned} & \frac{\cos \theta}{\frac{\mathrm{a}}{\mathrm{a}}}=\frac{\sin \theta}{\frac{\mathrm{b}}{\mathrm{b}}}=\frac{-1}{-\sqrt{2}} \\ & \cos \theta=\frac{1}{\sqrt{2}}=\sin \theta \\ & \therefore \theta=\frac{\pi}{4} \end{aligned} $
Practice questions
1. The sum of the squares of the reciprocals of two perpendicular diameter of an ellipse is
(a) $\frac{1}{4}\left(\frac{1}{\mathrm{a}^{2}}+\frac{1}{\mathrm{~b}^{2}}\right)$
(b) $\frac{1}{2}\left(\frac{1}{\mathrm{a}^{2}}+\frac{1}{\mathrm{~b}^{2}}\right)$
(c) $\frac{1}{\mathrm{a}^{2}}+\frac{1}{\mathrm{~b}^{2}}$
(d) None of these
Show Answer
Answer: (a)2. Prove that any point on the ellipse whose foci are $(-1,0)$ and $(7,0)$ and eccentcicity $\frac{1}{2}$ is $(3+8 \cos \theta, 4 \sqrt{3} \sin \theta), \theta \in R$. Also find the eq of the ellipse
Show Answer
Answer: $\frac{(x-3)^2}{64}+\frac{y^2}{48}=1$3. Let $\mathrm{E}$ be the ellipse $\frac{\mathrm{x}^{2}}{9}+\frac{\mathrm{y}^{2}}{4}=1$ and $\mathrm{C}$ be the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=9$. Let $\mathrm{P}$ and $\mathrm{Q}$ be the points
$(1,2)$ and $(2,1)$ respectively. Then
(a) $Q$ lies inside $\mathrm{C}$ but outside $\mathrm{E}$
(b) $\mathrm{Q}$ lies outside both $\mathrm{C}$ and $\mathrm{E}$
(c) $\mathrm{P}$ lies inside both $\mathrm{C}$ and $\mathrm{E}$
(d) $\mathrm{P}$ lies inside $\mathrm{C}$ but outside $\mathrm{E}$
Show Answer
Answer: (d)4. $\mathrm{P}$ is a variable on the ellipse $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ with $\mathrm{AA}^{\prime}$ as the major axis. Then the maximum area of the triangle $\mathrm{APA}^{\prime}$ is
(a) $\mathrm{ab}$
(b) $2 \mathrm{ab}$
(c) $\mathrm{ab} / 2$
(d) None of these
Show Answer
Answer: (a)5. A man running round a race course notes that the sum of the distances of two flag-posts from him is always $10 \mathrm{~m}$ and the distance between the flag-posts is $8 \mathrm{~m}$. The area of the path he encloses in square meters is
(a) $15 \pi$
(b) $12 \pi$
(c) $18 \pi$
(d) $8 \pi$
Show Answer
Answer: (a)6. If the line $\ell \mathrm{x}+\mathrm{my}+\mathrm{n}=0$ cuts the ellipse $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\frac{\mathrm{y}^{2}}{25}=1$ in points whose eccentric angles differ by $\frac{\pi}{2}$ then $\frac{\mathrm{a}^{2} \ell^{2}+\mathrm{b}^{2} \mathrm{~m}^{2}}{\mathrm{n}^{2}}$
(a) $1$
(b) $2$
(c) $4$
(d) $3 / 2$
Show Answer
Answer: (b)7. If $\mathrm{PSQ}$ is a focal chord if the ellipse $16 \mathrm{x}^{2}+25 \mathrm{y}^{2}=400$ such that $\mathrm{SP}=8$, then $\mathrm{SQ}=$
(a) 1
(b) 2
(c) 3
(d) 4
Show Answer
Answer: (b)8. If equation of the ellipse is $2 x^{2}+3 y^{2}-8 x+6 y+5=0$ then which of the following are true?
(a) equation of director circle is $x^{2}+y^{2}-4 x+2 y=10$
(b) director circle will pass through $(4,-1)$
(c) equation of auxillary circle is $x^{2}+y^{2}-4 x+2 y+2=0$
(d) None of these
Show Answer
Answer: (c)9. The foci of ellipse $\left(\frac{x}{5}\right)^{2}+\left(\frac{y}{3}\right)^{2}=1$ are $S$ and $S^{\prime}$. P is a point on ellipse whose eccentric angle is $\pi / 3$. The incentre of triangle $\mathrm{SPS}^{\prime}$ is
(a) $(2, \sqrt{3})$
(b) $\left(2, \frac{2}{\sqrt{3}}\right)$
(c) $\left(2, \frac{\sqrt{3}}{2}\right)$
(d) $(\sqrt{3}, 2)$





