Equation of a Hyperbola referred to two perpendicular lines

Let equation of hyperbola be

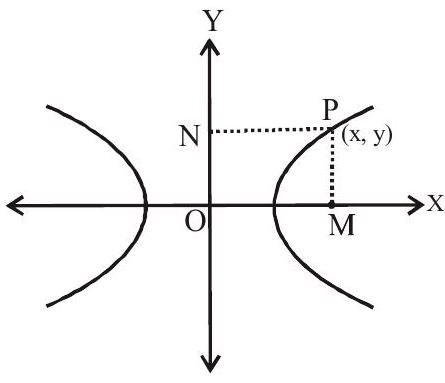
$\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$

From diagram $\mathrm{PM}=\mathrm{y}$ and $\mathrm{PN}=\mathrm{x}$

$\frac{\mathrm{PN}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{PM}^{2}}{\mathrm{~b}^{2}}=1$

ie. if perpendicular distance of a point $P(x, y)$ from two mutually perpendicular lines say $\ell _{1}=a _{1} x+b _{1} y+c _{1}=0$ and $\ell _{2}=\mathrm{a} _{2} \mathrm{x}+\mathrm{b} _{2} \mathrm{y}+\mathrm{c} _{2}=0$ then

$ \frac{\left(\frac{a _{1} x+b _{1} y+c _{1}}{\sqrt{a _{1}^{2}+b _{1}^{2}}}\right)}{a^{2}}-\frac{\left(\frac{a _{2} x+b _{2} y+c _{2}}{\sqrt{a _{2}^{2}+b _{2}^{2}}}\right)}{b^{2}}=1 $

then the locus of point $\mathrm{P}$ denotes a hyperbola

• centre of the hyperbola, we get after solving $\ell _{1}=0$ and $\ell _{2}=0$

• Transverse axis : $\ell=0$

• Conjugate axis $: \ell _{1}=0$

• Foci : The foci of the hyperbola is the point of intersection of the lines $\frac{a _{1} x+b _{1} y+c _{1}}{\sqrt{a _{1}^{2}+b _{1}^{2}}}= \pm a e$ and $\ell _{2}=0$

• Directrix: $\frac{a _{1} x+b _{1} y+c _{1}}{\sqrt{a _{1}^{2}+b _{1}^{2}}}= \pm \frac{a}{e}$

• Length of transverse axis $=2 \mathrm{a}$

• Length of conjugate axis $=2 b$

• Length of latus Rectum $=\frac{2 b^{2}}{a}$

Examples

1. Find the eccentricity and centre of the hyperbola

$ \frac{(3 x-4 y-12)^{2}}{100}-\frac{(4 x+3 y-12)^{2}}{225}=1 $

2. Find the eccentricity of the conic $4(2 y-x-3)^{2}-9(2 x+y-1)^{2}=80$

3. Find the coordinates of the centre, foci and vertices, length of axes and latus rectum, equation of axes and directries, and eccentricity of the conic $9 x^{2}-16 y^{2}-18 x+32 y-151=0$

4. The equation of the transverse and conjugate axes of a hyperbola are respectively $3 x+4 y-7=0$, $4 x-3 y+8=0$ and their respective lengths are 4 and 6 . The equation of the hyperbola is

(a). $ 17 x^{2}+312 x y+108 y^{2}-634 x-312 y-715=0$

(b). $ 108 x^{2}+312 x y+17 y^{2}-312 x-634 y-715=0$

(c). $108 x^{2}-312 x y+17 y^{2}-312 x-634 y-715=0$

(d). none of these

Line and Hyperbola

Let equation of line be $y=m x+c$ and equation of hyperbola be $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$

$ \begin{aligned} & \frac{x^{2}}{a^{2}}-\frac{(m x+c)^{2}}{b^{2}}=1 \\ & \frac{x^{2}}{a^{2}}-\frac{m^{2} x^{2}}{b^{2}}-\frac{c^{2}}{b^{2}}-\frac{2 m c}{b^{2}} x-1=0 \\ & x^{2}\left(\frac{1}{a^{2}}-\frac{m^{2}}{b^{2}}\right)-\frac{2 m c}{b^{2}} x-\left(\frac{c^{2}+b^{2}}{b^{2}}\right)=0 \\ & x^{2}\left(\frac{b^{2}}{a^{2}}-m^{2}\right)-2 m c x-\left(c^{2}+b^{2}\right)=0 \end{aligned} $

$\therefore \mathrm{D}=4 \mathrm{~m}^{2} \mathrm{c}^{2}+4 \cdot\left(\frac{\mathrm{b}^{2}-\mathrm{a}^{2} \mathrm{~m}^{2}}{\mathrm{a}^{2}}\right)\left(\mathrm{c}^{2}+\mathrm{b}^{2}\right)=4\left(\mathrm{~m}^{2} \phi^{2}+\frac{\mathrm{b}^{2}}{\mathrm{a}^{2}} \mathrm{c}^{2}-\mathrm{m}^{2} \phi^{2}+\frac{\mathrm{b}^{4}}{\mathrm{a}^{2}}-\mathrm{m}^{2} \mathrm{~b}^{2}\right)=4 \mathrm{~b}^{2}\left(\frac{\mathrm{c}^{2}+\mathrm{b}^{2}-\mathrm{a}^{2} \mathrm{~m}^{2}}{\mathrm{a}^{2}}\right)$

i. $\quad \mathrm{D}<0$ i.e. $\mathrm{c}^{2}-\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{b}^{2}<0$ line do not intersect hyperbola .

ii. $\quad \mathrm{D}=0$ i.e. $\mathrm{c}^{2}-\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{b}^{2}=0$ line touches the hyperbola .

iii. $\quad \mathrm{D}>0$ i.e. $\mathrm{c}^{2}-\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{b}^{2}>0$ line intersect hyperbola at two points.

Hence $y=m x \pm \sqrt{a^{2} m^{2}-b^{2}}$ is a tangent to hyperbola .

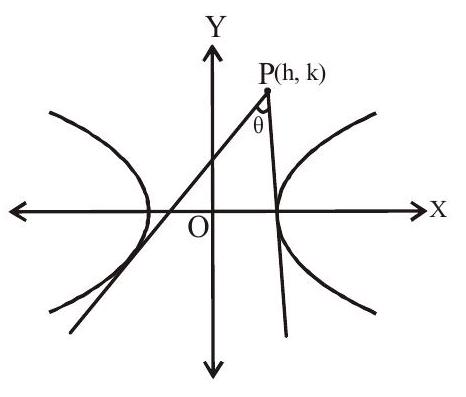
Let this tangent passes through a point $(\mathrm{h}, \mathrm{k})$ then $\mathrm{k}=\mathrm{mh} \pm \sqrt{\mathrm{a}^{2} \mathrm{~m}^{2}-\mathrm{b}^{2}}$ $(\mathrm{k}-\mathrm{mh})^{2}=\mathrm{a}^{2} \mathrm{~m}^{2}-\mathrm{b}^{2}$

$\mathrm{m}^{2}\left(\mathrm{~h}^{2}-\mathrm{a}^{2}\right)-2 \mathrm{mkh}+\mathrm{k}^{2}+\mathrm{b}^{2}=0$

Hence maximum two tangents can be drawn through a point $P$.

Now $\mathrm{m} _{1}+\mathrm{m} _{2}=\frac{2 \mathrm{kh}}{\mathrm{h}^{2}-\mathrm{a}^{2}}$

$\mathrm{m} _{1} \cdot \mathrm{m} _{2}=\frac{\mathrm{k}^{2}+\mathrm{b}^{2}}{\mathrm{~h}^{2}-\mathrm{a}^{2}}$

If $\theta$ is the angle between the two tangents, then

$\tan \theta=\left(\frac{\mathrm{m} _{1}-\mathrm{m} _{2}}{1+\mathrm{m} _{1} \mathrm{~m} _{2}}\right)$

$\Rightarrow \tan ^{2} \theta=\frac{\left(m _{1}+m _{2}\right)^{2}-4 m _{1} m _{2}}{\left(1+m _{1} m _{2}\right)^{2}}=\frac{\left(\frac{2 k h}{h^{2}-a^{2}}\right)^{2}-4\left(\frac{k^{2}+b^{2}}{h^{2}-a^{2}}\right)}{\left(1+\frac{k^{2}+b^{2}}{h^{2}-a^{2}}\right)^{2}}$

$\Rightarrow \tan ^{2} \theta=\frac{4 \mathrm{k}^{2} \mathrm{~h}^{2}-4\left(\mathrm{~h}^{2}-\mathrm{a}^{2}\right)\left(\mathrm{k}^{2}+\mathrm{b}^{2}\right)}{\left(\mathrm{h}^{2}+\mathrm{k}^{2}-\mathrm{a}^{2}+\mathrm{b}^{2}\right)^{2}}$

$\Rightarrow \tan ^{2} \theta=\frac{4\left(\mathrm{a}^{2} \mathrm{~b}^{2}+\mathrm{a}^{2} \mathrm{k}^{2}-\mathrm{h}^{2} \mathrm{~b}^{2}\right)}{\left(\mathrm{h}^{2}+\mathrm{k}^{2}-\mathrm{a}^{2}+\mathrm{b}^{2}\right)^{2}}$

If $\theta=90^{\circ}$ then $\mathrm{h}^{2}+\mathrm{k}^{2}-\mathrm{a}^{2}+\mathrm{b}^{2}=0$

i.e. $\mathrm{h}^{2}+\mathrm{k}^{2}=\mathrm{a}^{2}-\mathrm{b}^{2}$

Locus of $(h, k)$ is $x^{2}+y^{2}=a^{2}-b^{2}$

Hence, Locus of point of intersection of two perpendicular tangents is known as Director Circle. Its equation is $x^{2}+y^{2}=a^{2}-b^{2}$

If $\mathrm{a}=\mathrm{b}$, director circle is a point circle.

If $a<b$, no real director circle is possible.

For equation of hyperbola $\frac{(x-h)^{2}}{a^{2}}-\frac{(y-h)^{2}}{b^{2}}=1$, equation of tangent in slope from is $y-k=m(x-$h) $\pm \sqrt{a^{2} m^{2}-b^{2}}$.

Practice questions

1. If the foci of the ellipse $\frac{\mathrm{x}^{2}}{232}+\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ and the hyperbola $\frac{\mathrm{x}^{2}}{144}-\frac{\mathrm{y}^{2}}{81}=1$ coincide then $\mathrm{b}^{2}=$

(a). 3

(b). 5

(c). 7

(d). 9

2. If $\mathrm{PQ}$ is a double ordinate of the hyperbola $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ such that $\mathrm{OPQ}$ is an equilateral triangle, $O$ being the centre of the hyperbola, the range of eccentricity is

(a). $\left(0, \frac{2}{\sqrt{3}}\right)$

(b). $\left(\frac{2}{\sqrt{3}}, \infty\right)$

(c). $\left(0, \frac{4}{3}\right)$

(d). $\left(\frac{4}{3}, \infty\right)$

3. An ellipse and hyperbola are confocal and the conjugate axis of the hyperbola is equal to the minor axis of the ellipse. If $\mathrm{e} _{1}$ and $\mathrm{e} _{2}$ are the eccentricities of the ellipse and hyperbola then

(a). $\mathrm{e} _{1}{ }^{2}+\mathrm{e} _{2}{ }^{2}=2$

(b). $\mathrm{e} _{1}+\mathrm{e} _{2}=2$

(c). $\frac{1}{\mathrm{e} _{1}}+\frac{1}{\mathrm{e} _{2}}=2$

(d). $\frac{1}{\mathrm{e} _{1}^{2}}+\frac{1}{\mathrm{e} _{2}^{2}}=2$

4. The centre of a hyperbola $\frac{(3 x+4 y-7)^{2}}{100}-\frac{(4 x-3 y+8)^{2}}{225}=1$ is

(a). $\left(\frac{-11}{25}, \frac{52}{25}\right)$

(b). $\left(\frac{11}{25}, \frac{-52}{25}\right)$

(c). $(0,0)$

(d). $(10,15)$

5. The equations of the transverse and conjugate axes of a hyperbola are $x+2 y-3=0$ and $2 x-y+4=0$ respectively and their respective lengths are $\sqrt{2}$ and $\frac{2}{\sqrt{3}}$, equation of hyperbola is

(a). $ 2(2 x-y+4)^{2}-3(x+2 y-3)^{2}=1$

(b). $2(x+2 y-3)^{2}-3(2 x-y+4)^{2}=1$

(c). $ 2(2 x-y+4)^{2}-3(x+2 y-3)^{2}=5$

(d). $2(x+2 y-3)^{2}-3(2 x-y+4)^{2}=5$

6. For all real values of $m$ the straight line $y=m x+\sqrt{9 m^{2}-4}$ is a tangent to the hyperbola

(a). $4 x^{2}-9 y^{2}=36$

(b). $9 x^{2}-4 y^{2}=36$

(c). $x^{2}-36 y^{2}=9$

(d). $36 x^{2}-y^{2}=36$

7. The equation of tangents to the curve $4 x^{2}-9 y^{2}=1$ which is parallel to $4 y=5 x+7$ is

(a). $4 y=5 x-30$

(b). $4 y=5 x+24$

(c). $24 \mathrm{y}-30 \mathrm{x}=\sqrt{161}$

(d). $30 \mathrm{x}-24 \mathrm{y}-\sqrt{161}=0$

8. If the line $5 x+12 y=9$ touches the hyperbola $x^{2}-9 y^{2}=9$ then point of contact is

(a). $(5,4)$

(b). $\left(5, \frac{-4}{3}\right)$

(c). $\left(5, \frac{4}{3}\right)$

(d). $(5,-4)$

9. If $\mathrm{y}=\mathrm{mx}+\sqrt{51}$ is a tangent to the hyperbola $\frac{\mathrm{x}^{2}}{100}-\frac{\mathrm{y}^{2}}{49}=1$, then $\mathrm{m}=$

(a). $1$

(b). $\sqrt{17}$

(c). $-1$

(d). $2$

10. The locus of the point of intersection of perpendicular tangents to $\frac{x^{2}}{25}-\frac{y^{2}}{16}=1$ is:

(a). $ x^2+y^2=25$

(b). $x^2+y^2=16$

(c). $x^2+y^2=41$

(d). $x^2+y^2=9$