HYPERBOLA- 4 (Equation of Tangent)
Equation of Tangent
i. Point Form
$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$
Differentiate w.r.t. $\mathrm{x}$
$ \begin{aligned} & \frac{2 x}{a^{2}}-\frac{2 y}{a _{2}} \frac{d y}{d x}=0 \\ & \frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{b}^{2} \mathrm{x}}{\mathrm{b}^{2} \mathrm{y}} \end{aligned} $
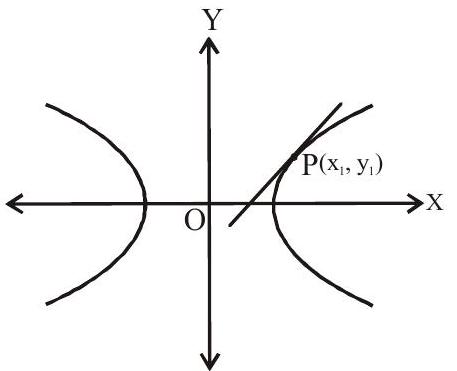
Slope of tangent $=\frac{b^{2} x _{1}}{a^{2} y _{1}}$
Equation of tangent, $y-y _{1}=\frac{b^{2} x _{1}}{a^{2} y _{1}}\left(x-x _{1}\right)$
$\frac{\mathrm{xx} _{1}}{\mathrm{a}^{2}}-\frac{\mathrm{yy} _{1}}{\mathrm{~b}^{2}}=\frac{\mathrm{x} _{1}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y} _{1}^{2}}{\mathrm{~b}^{2}}$
$\frac{\mathrm{xx} _{1}}{\mathrm{a}^{2}}-\frac{\mathrm{yy} _{1}}{\mathrm{~b}^{2}}=1\left(\text { But } \mathrm{P}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)\right.$ lies on hyperbola$)$
or $\mathrm{T}=\frac{\mathrm{xx} _{1}}{\mathrm{a}^{2}}-\frac{\mathrm{yy} _{1}}{\mathrm{~b}^{2}}-1$
Equation of tangent is $\mathrm{T}=0$
Equation of tangent at point $\mathrm{P}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ to the hyperbola $\frac{(\mathrm{x}-\mathrm{h})^{2}}{\mathrm{a}^{2}}-\frac{(\mathrm{y}-\mathrm{k})^{2}}{\mathrm{~b}^{2}}=1$ is $\frac{(\mathrm{x}-\mathrm{h})\left(\mathrm{x} _{1}-\mathrm{h}\right)}{\mathrm{a}^{2}}-\frac{(\mathrm{y}-\mathrm{k})\left(\mathrm{y} _{1}-\mathrm{k}\right)}{\mathrm{b}^{2}}=1$
ii. Parametric Form
Parametric equation of hyperbola is $x=a \sec \theta, y=b \tan \theta$
Equation of tangent is
$ \frac{x}{a} \sec \theta-\frac{y}{b} \tan \theta=1 $
iii. Slope Form
$ y=m x \pm \sqrt{a^{2} m^{2}-b^{2}} $
| Hyperbola: $\left(\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1\right)$ | Point of contact. |
| Point form : $\frac{\mathrm{xx} _{1}}{\mathrm{a}^{2}}-\frac{\mathrm{yy} _{1}}{\mathrm{~b}^{2}}=1 $ | $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ |
| Parametric Form : $\frac{\mathrm{x}}{\mathrm{a}} \sec \theta-\frac{\mathrm{y}}{\mathrm{b}} \tan \theta=1 $ | $ (a \sec \theta, \mathrm{b\tan} \theta )$ |
| Slope form: $\mathrm{y}=\mathrm{mx} _{ \pm} \sqrt{\mathrm{a}^{2} \mathrm{~m}^{2}-\mathrm{b}^{2}} $ | $\left( \pm \frac{\mathrm{a}^{2} \mathrm{~m}}{\sqrt{\mathrm{a}^{2} \mathrm{~m}^{2}-\mathrm{b}^{2}}}, \pm \frac{\mathrm{b}^{2}}{\sqrt{\mathrm{a}^{2} \mathrm{~m}^{2}-\mathrm{b}^{2}}}\right)$ |
Examples
1. The equation of a tangent to the hyperbola $16 x^{2}-25 y^{2}-96 x+100 y-356=0$, which makes an angle $\frac{\pi}{4}$ with the transverse axis, is
(a). $\mathrm{y}=\mathrm{x}+2$
(b). $\mathrm{y}=\mathrm{x}-5$
(c). $\mathrm{y}=\mathrm{x}+3$
(d). $x=y+2$
Show Answer
Solution:
The equation of the hyperbola is
$ \begin{aligned} & 16\left(x^{2}-6 x\right)-25\left(y^{2}-4 y\right)=356 \\ & \frac{(x-3)^{2}}{25}-\frac{(y-2)^{2}}{16}=1 \end{aligned} $
The equation of tangent of slope $m=\tan \frac{\pi}{4}=1$ to this hyperbola are
$ \begin{aligned} & y-2=1(x-3) \pm \sqrt{25 \times 1-16} \\ & y-2=x-3 \pm 3 \\ & \Rightarrow y=x+2 \text { or } y=x-4 \end{aligned} $
Answer: (a)
2. The point of intersection of two tangents to the hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$, the product of whose slopes is $\mathrm{c}^{2}$, lies on the curve
(a). $\mathrm{y}^{2}-\mathrm{b}^{2}=\mathrm{c}^{2}\left(\mathrm{x}^{2}+\mathrm{a}^{2}\right)$
(b). $\mathrm{y}^{2}+\mathrm{a}^{2}=\mathrm{c}^{2}\left(\mathrm{x}^{2}-\mathrm{b}^{2}\right)$
(c). $\mathrm{y}^{2}+\mathrm{b}^{2}=\mathrm{c}^{2}\left(\mathrm{x}^{2}-\mathrm{a}^{2}\right)$
(d). $\mathrm{y}^{2}-\mathrm{a}^{2}=\mathrm{c}^{2}\left(\mathrm{x}^{2}+\mathrm{b}^{2}\right)$
Show Answer
Solution:
Let $\mathrm{P}(\mathrm{h}, \mathrm{k})$ be the point of intersection of two tangents to the hyperbola $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ The equation of tangent to hyperbola is
$ \mathrm{y}=\mathrm{mx} \pm \sqrt{\mathrm{a}^{2} \mathrm{~m}^{2}-\mathrm{b}^{2}} $
If it passes through $(\mathrm{h}, \mathrm{k})$ then
$\mathrm{k}=\mathrm{mh} \pm \sqrt{\mathrm{a}^{2} \mathrm{~m}^{2}-\mathrm{b}^{2}}$
$\Rightarrow(\mathrm{k}-\mathrm{mh})^{2}=\mathrm{a}^{2} \mathrm{~m}^{2}-\mathrm{b}^{2}$
$\Rightarrow \mathrm{m}^{2}\left(\mathrm{~h}^{2}-\mathrm{a}^{2}\right)-2 \mathrm{mkh}+\mathrm{k}^{2}+\mathrm{b}^{2}=0$
Let $m _{1}$ and $m _{2}$ be the slopes of the tangents passing throgh $P$. Then $m _{1} \cdot m _{2}=\frac{k^{2}+b^{2}}{h^{2}-a^{2}}$
$\Rightarrow \mathrm{c}^{2}=\frac{\mathrm{k}^{2}+\mathrm{b}^{2}}{\mathrm{~h}^{2}-\mathrm{a}^{2}}$
Hence locus of $\mathrm{P}(\mathrm{h}, \mathrm{k})$ is $\mathrm{y}^{2}+\mathrm{b}^{2}=\left(\mathrm{x}^{2}-\mathrm{a}^{2}\right) \mathrm{c}^{2}$
Answer: (c)
3. If the tangents drawn from a point on the hyperbola $x^{2}-y^{2}=a^{2}-b^{2}$ to the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ make angles $\alpha$ and $\beta$ with the transverse axis of the hyperbola, then
(a). $\tan \alpha-\tan \beta=1$
(b). $\tan \alpha+\tan \beta=1$
(c). $\tan \alpha \cdot \tan \beta=1$
(d). $\tan \alpha \cdot \tan \beta=-1$
Show Answer
Solution:
Let $\mathrm{P}(\mathrm{h}, \mathrm{k})$ be the point on the hyperbola $\mathrm{x}^{2}-\mathrm{y}^{2}=\mathrm{a}^{2}-\mathrm{b}^{2}$, then $\mathrm{h}^{2}-\mathrm{k}^{2}=\mathrm{a}^{2}-\mathrm{b}^{2}…….(i)$
The equation of tangent to the ellipse is $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ is
$y=m x \pm \sqrt{a^{2} m^{2}+b^{2}}$
If it passes through $(\mathrm{h}, \mathrm{k})$ then
$\mathrm{k}=\mathrm{mh} \pm \sqrt{\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{b}^{2}}$
$(\mathrm{k}-\mathrm{mh})^{2}=\mathrm{a}^{2} \mathrm{~m}^{2}+\mathrm{b}^{2}$
$\mathrm{m}^{2}\left(\mathrm{~h}^{2}-\mathrm{a}^{2}\right)-2 \mathrm{mkh}+\mathrm{k}^{2}-\mathrm{b}^{2}=0$
Let $\mathrm{m} _{1}$ and $\mathrm{m} _{2}$ be the roots of this equation, then
$\mathrm{m} _{1} \cdot \mathrm{m} _{2}=\frac{\mathrm{k}^{2}-\mathrm{b}^{2}}{\mathrm{~h}^{2}-\mathrm{a}^{2}}=1$ (from equation (i))
$\tan \alpha \cdot \tan \beta=1$
Answer: (c)
4. If the line $2 x+\sqrt{6} y=2$ touches the hyperbola $x^{2}-2 y^{2}=4$, then the point of contact is
(a). $(-2, \sqrt{6})$
(b). $(-5,2 \sqrt{6})$
(c). $\left(\frac{1}{2}, \frac{1}{\sqrt{6}}\right)$
(d). $(4,-\sqrt{6})$
Show Answer
Solution:
Equation of hyperbola is $\frac{x^{2}}{(2)^{2}}-\frac{y^{2}}{(\sqrt{2})^{2}}=1$
Equation of tangent is $\mathrm{y}=-\sqrt{\frac{2}{3}} \mathrm{x}+\sqrt{\frac{2}{3}}$
$m=-\sqrt{\frac{2}{3}}, a=2, b=\sqrt{2}, c=\sqrt{\frac{2}{3}}$ and $c^{2}=a^{2} m^{2}-b^{2}$
Point of contact is $\left( \pm \frac{a^{2} m}{\sqrt{a^{2} m^{2}-b^{2}}}, \pm \frac{b^{2}}{\sqrt{a^{2} m^{2}-b^{2}}}\right)$ i.e. $(\mp 4, \pm \sqrt{6})$
Answer: (d)
5. Number of real tangents can be drawn from the point $(5,0)$ to the hyperbola $\frac{x^{2}}{16}-\frac{y^{2}}{9}=1$ is
(a). 2
(b). 1
(c). 0
(d). 4
Show Answer
Solution:
$\mathrm{S} _{1}=\frac{25}{16}-\frac{0}{9}-1>0$
$\therefore$ Point $(5,0)$ lies inside the hyperbola. Hence no tangents can be drawn.
Answer: (c)
Practice questions
1. $\mathrm{P}$ is a point on the hyperbola $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1, \mathrm{~N}$ is the foot of the perpendicuilar from $\mathrm{P}$ on the transverse axis. The tangent to the hyperbola at $\mathrm{P}$ meets the transverse axis at $\mathrm{T}$. If $\mathrm{O}$ is the centre of the hyperbola, then $\mathrm{OT} \times \mathrm{ON}$ is
(a). $b^{2}$
(b). $ a^{2}$
(c). $a b$
(d). none of these
Show Answer
Answer: (b)2. Tangents drawn from the point (c,d) to the hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ make angles $\alpha$ and $\beta$ with the $\mathrm{x}$-axis. If $\tan \alpha \tan \beta=1$, then $\mathrm{c}^{2}-\mathrm{d}^{2}=$
(a). $ a^{2}-b^{2}$
(b). $ a^{2} \cdot b^{2}$
(c). $a^{2}+b^{2}$
(d). none of these
Show Answer
Answer: (c)3. The common tangents to the two hyperbolas $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ and $\frac{\mathrm{y}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{x}^{2}}{\mathrm{~b}^{2}}=1$ is
(a). $\mathrm{y}=\mathrm{x}+\sqrt{\mathrm{a}^{2}-\mathrm{b}^{2}}$
(b). $y=x+\sqrt{a^{2}+b^{2}}$
(c). $y=2 x+\sqrt{a^{2}-b^{2}}$
(d). none of these
Show Answer
Answer: (a)4. The equation of the tangent to the curve $4 x^{2}-9 y^{2}=1$ which is parallel to $4 y=5 x+7$ is
(a). $30 x+24 y=720$
(b). $7 y=6 x-15$
(c). $y=3 \sqrt{\frac{2}{7}} x+\frac{15}{\sqrt{7}}$
(d). none of these
Show Answer
Answer: (d)5. The locus of a point $\mathrm{P}(\mathrm{h}, \mathrm{k})$ moving under the condition that the line $\mathrm{y}=\mathrm{hx}+\mathrm{k}$ is a tangent to the hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ is
(a). Parabola
(b). circle
(c). ellipse
(d). hyperbola





