Practice problems

1. Equation of conjugate axis of hyperbola $x y-3 y-4 x+7=0$ is

(a) $x+y=7$

(b) $x+y=3$

(c) $\mathrm{x}-\mathrm{y}=7$

(d) None of these

Show Answer

Solution:

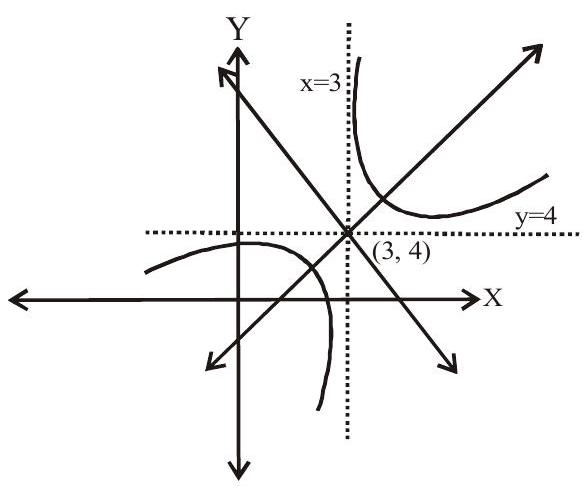
$ \begin{aligned} & x y-3 y-4 x+7=0 \\ & x y-3 y-4 x+12=5 \\ & (x-3)(y-4)=5 \end{aligned} $

Equation of asymptotes are $x-3=0$ and $y-4=0$ Since the hyperbola is rectangular hyperbola, axes are bisectors of asymptotes

Hence their slopes are $\pm 1$

$\therefore$ Equation of conjugate axis is

$ \begin{aligned} & y-4=-1(x-3) \\ & x+y=7 \end{aligned} $

Answer: (a)

2. If $S _{1}$ and $S _{2}$ are the foci of the hyperbola whose transverse axis length is 4 and conjugate axis length is $6, S _{3}$ and $\mathrm{S} _{4}$ are the foci of the conjugate hyperbola, then the area of the quadrilateral $\mathrm{S} _{1} \mathrm{~S} _{3} \mathrm{~S} _{2} \mathrm{~S} _{4}$ is

(a) 156

(b) 36

(c) 26

(d) None of these

Show Answer

Solution :

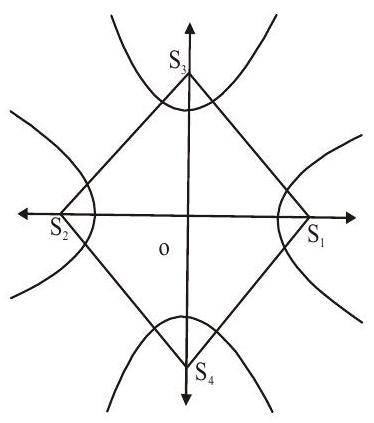
$\mathrm{S} _{1} \mathrm{~S} _{3} \mathrm{~S} _{2} \mathrm{~S} _{4}$ forms a square.

So required area $=4 \times$ area of ${ } _{\Delta} \mathrm{S} _{1} \mathrm{OS} _{3}=4 \times \frac{1}{2}$ ae $\times \mathrm{be} _{1}$

$ \begin{aligned} & =2 \mathrm{abee} _{1}=2.2 .3 . \mathrm{e} \mathrm{e} _{1} \\ & =12 \mathrm{ee} _{1} \end{aligned} $

Now e $=\sqrt{1+\frac{9}{4}}=\frac{\sqrt{13}}{2} \& \mathrm{e} _{1}=\sqrt{1+\frac{9}{4}}=\frac{\sqrt{13}}{2}$

Hence area $=12 \times \frac{\sqrt{13}}{2} \times \frac{\sqrt{13}}{2}=26$ sq.units

Answer: (c)

3. The ellipse $4 x^{2}+9 y^{2}=36$ and the hyperbola $a^{2} x^{2}-y^{2}=4$ intersect at right angles then the equation of the circle through the points of intersection of two conic is

(a) $x^{2}+y^{2}=25$

(c) $5\left(x^{2}+y^{2}\right)-3 x-4 y=0$

(b) $5\left(x^{2}+y^{2}\right)+3 x+4 y=0$

(d) $\left(x^{2}+y^{2}\right)=5$

Show Answer

Solution:

Since ellipse and hyperbola intersect orthogonally, they are confocal.

$ \mathrm{e}=\sqrt{1-\frac{4}{9}}=\frac{\sqrt{5}}{3} $

foci of ellipse $( \pm \sqrt{5}, 0)$

$(a)^{2}=a^{2}+b^{2}$

$ 5=\frac{4}{a^{2}}+4 \Rightarrow a=2 $

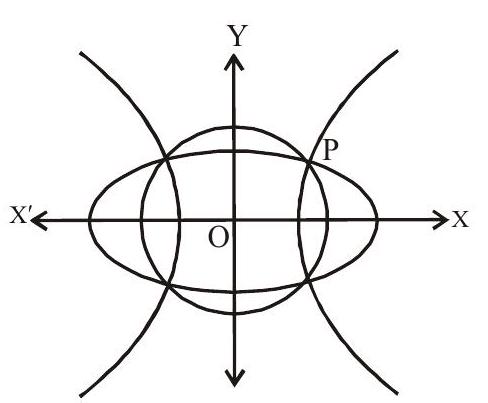
Let point of intersection in the first quadrant be $\mathrm{P}\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$.

$\mathrm{P}$ lies on both the curves.

$4x _{1}^{2}+9 y _{1}^{2}=36 \quad \text { and } 4 x _{1}^{2}-y _{1}^{2}=4$

Adding these two, we get $8 \mathrm{x} _{1}{ }^{2}+8 \mathrm{y} _{1}{ }^{2}=40$

$ \mathrm{x} _{1}^{2}+\mathrm{y} _{1}^{2}=5 $

Equation of circle is $x^{2}+y^{2}=5$

4. If $\mathrm{e}$ is the eccentricity of the hyperbola $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ and $2 \theta$ is angle between the asymptotes then $\cos \theta=$

(a) $\frac{1}{\mathrm{e}}$

(b) $\frac{1-e}{e}$

(c) $\frac{1+\mathrm{e}}{\mathrm{e}}$

(d) None of these

5. From a point $p(1,2)$ pair of tangents are drawn to a hyperbola in which one tangent to each arm of hyperbola. Equation of asymptotes of hyperbola are $\sqrt{3} x-y+5=0$ and $\sqrt{3} x+y-1=0$ then eccentricity of hyperbola is

(a) $\sqrt{3}$

(b) $\frac{2}{\sqrt{3}}$

(c) $2$

(d) None of these

Show Answer

Solution:

Equation of asymptotes are

$\sqrt{3} \mathrm{x}-\mathrm{y}+5=0$

$-\sqrt{3} \mathrm{x}-\mathrm{y}+1=0$

$\therefore \mathrm{a} _{1} \mathrm{a} _{2}+\mathrm{b} _{1} \mathrm{~b} _{2}=-3+1<0$

$\therefore$ origin lies in acute angle and $\mathrm{P}(1,2)$ lies in obtuse angle.

$\therefore \mathrm{e}=\sec \theta$ where $2 \theta$ is the angle between asymptotes.

$2 \theta=\frac{\pi}{3} \Rightarrow \theta=\frac{\pi}{6}$

$ \mathrm{e}=\sec \frac{\pi}{6}=\frac{2}{\sqrt{3}} $

Answer: (b)

6. If a variable line has its intercepts on the coordinate axes $\mathrm{e}, \mathrm{e}^{\prime}$ where $\frac{\mathrm{e}}{2}, \frac{\mathrm{e}^{\prime}}{2}$ are the eccentricities of a hyperbola and its conjugate hyperbola, then the line always touches the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=\mathrm{r}^{2}$, where $\mathrm{r}=$

(a) $4$

(b) $3$

(c) $2$

(d) Can not be decided

7. If angle between asymptotes of hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ is $120^{\circ}$ and product of perpendiculars drawn from foci upon its any tangent is 9 , then locus of point of intersection of perpendicular tangents of the hyperbola can be

(a) $x^{2}+y^{2}=18$

(b) $\mathrm{x}^{2}+\mathrm{y}^{2}=6$

(c) $\mathrm{x}^{2}+\mathrm{y}^{2}=9$

(d) $\mathrm{x}^{2}+\mathrm{y}^{2}=3$

8. The equation of the transverse axis of the hyperbola

$(x-3)^{2}+(y+1)^{2}=(4 x+3 y)^{2}$ is

(a) $3 x-4 y=0$

(b) $4 x+3 y=0$

(c) $3 x-4 y=13$

(d) $4 x+3 y=9$

Practice questions

1. The equation of common tangents to the parabola $y^{2}=8 x$ and hyperbola $3 x^{2}-y^{2}=3$ is

(a) $x \pm 2 y-1=0$

(b) $x \pm 2 y+1=0$

(c) $2 \mathrm{x} \pm \mathrm{y}+1=0$

(d) $2 \mathrm{x} \pm \mathrm{y}-1=0$

2. A tangent to the hyperbola $y=\frac{x+9}{x+5}$ passing through the origin is

(a) $x-2 y=0$

(b) $5 x-y=0$

(c) $5 \mathrm{x}+\mathrm{y}=0$

(d) $x+225 y=0$

3. The equation of the common tangent to the curves $y^{2}=8 x$ and $x y=-1$ is

(a) $y=x+2$

(b) $y=2 x+1$

(c) $2 y=x+8$

(d) $3 y=9 x+2$

4. Let $\mathrm{PQ}$ be a double ordinate of the hyperbola $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$. If $\mathrm{O}$ be the centre of the hyperbola and $\mathrm{OPQ}$ is an equilateral triangle, then eccentricity e is

(a) $>\sqrt{3}$

(b) $>2$

(c) $>\frac{2}{\sqrt{3}}$

(d) None of these

5. The difference between the length $2 \mathrm{a}$ of the transverse axis of a hyperbola of eccentricity e and the length of its latus rectum is

(a) $\mathrm{a}\left(2 \mathrm{e}^{2}-1\right)$

(b) $2 \mathrm{a}\left(\mathrm{e}^{2}-1\right)$

(c) $2 \mathrm{a}\left|3-\mathrm{e}^{2}\right|$

(d) $2 \mathrm{a}\left|2-\mathrm{e}^{2}\right|$

6. The slopes of common tangents to the hyperbolas $\frac{\mathrm{x}^{2}}{9}-\frac{\mathrm{y}^{2}}{16}=1$ and $\frac{\mathrm{y}^{2}}{9}-\frac{\mathrm{x}^{2}}{16}=1$ are

(a) $\pm 2$

(b) $\pm \sqrt{2}$

(c) $\pm 1$

(d) None of these

7. The two conics $\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}=1$ and $y^{2}=-\frac{b}{a} x$ intersect if $f$

(a) $0<\mathrm{b} \leq \frac{1}{2}$

(b) $0<\mathrm{a} \leq \frac{1}{2}$

(c) b $^{2}<\mathrm{a}^{2}$

(d) $b^{2}>a^{2}$

8. The point on the hyperbola $\frac{x^{2}}{24}-\frac{y^{2}}{18}=1$ which is nearest to the line $3 x+2 y+1=0$ is

(a) $(-6,3)$

(b) $(3,-6)$

(c) $(-6,-3)$

(d) $(6,3)$

9. If $(\operatorname{asec} \theta, b \tan \theta)$ and $(\operatorname{asec} \phi, b \tan \phi)$ be the coordinates of the ends of a focal chord of the hyperbola $\frac{\mathrm{x}^{2}}{\mathrm{a}^{2}}-\frac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$, then $\tan \frac{\theta}{2} \tan \frac{\phi}{2}=$

(a) $\frac{1+\mathrm{e}}{1-\mathrm{e}}$

(b) $\frac{1-\mathrm{e}}{1+\mathrm{e}}$

(c) $\frac{\mathrm{e}-1}{\mathrm{e}+1}$

(d) None of these

10. If the latus rectum of a hyperbola through one focus subtends $60^{\circ}$ angle at the other focus, then its eccentricity e is

(a) $\sqrt{2}$

(b) $\sqrt{3}$

(c) $\sqrt{5}$

(d) $\sqrt{6}$