PARABOLA-3
Parametric form
| $y^{2}=4 a x$ | $y^{2}=-4 a x$ | $x^{2}=4 a y$ | $x^{2}=-4 a y$ |
|---|---|---|---|
| $x=a t^{2}$ | $x=-a t^{2}$ | $x=2 a t$ | $x=2 a t$ |
| $y=2 a t$ | $y=2 a t$ | $y=a t^{2}$ | $y=-a t^{2}$ |
| $\left(a t^{2}, 2 a t\right)$ | $\left(-a t^{2}, 2 a t\right)$ | $\left(2 a t, a t^{2}\right)$ | $\left(2 a t,-a t^{2}\right)$ |
Properties of Focal chord:
1. If the chord joining $\mathrm{P}\left(\mathrm{t} _{1}\right)$ and $\mathrm{Q}\left(\mathrm{t} _{2}\right)$ is the focal chord then $\mathrm{t} _{1} \cdot \mathrm{t} _{2}=-1$.
$\mathrm{P}, \mathrm{S}$ and $\mathrm{Q}$ lies on the focal chord
$\therefore \quad \mathrm{P}, \mathrm{S}$ and $\mathrm{Q}$ are collinear slope of PS = slope of SQ
$ \begin{aligned} & \frac{2 \mathrm{at} _{1}}{\mathrm{at} _{1}^{2}-\mathrm{a}}=\frac{2 \mathrm{at} _{2}}{\mathrm{at} _{2}^{2}-\mathrm{a}} \\ & \frac{2 \mathrm{t} _{1}}{\mathrm{t} _{1}^{2}-1}=\frac{2 \mathrm{t} _{2}}{\mathrm{t} _{2}^{2}-1} \\ & \mathrm{t} _{1} \mathrm{t} _{2}^{2}-\mathrm{t} _{1}=\mathrm{t} _{2} \mathrm{t} _{1}^{2}-\mathrm{t} _{2} \\ & \mathrm{t} _{2}-\mathrm{t} _{1}=\mathrm{t} _{1} \mathrm{t} _{2}\left(\mathrm{t} _{1}-\mathrm{t} _{2}\right) \\ & -1=\mathrm{t} _{1} \mathrm{t} _{2} \quad \text { or } \quad \mathrm{t} _{2}=-\frac{1}{\mathrm{t} _{1}} \end{aligned} $
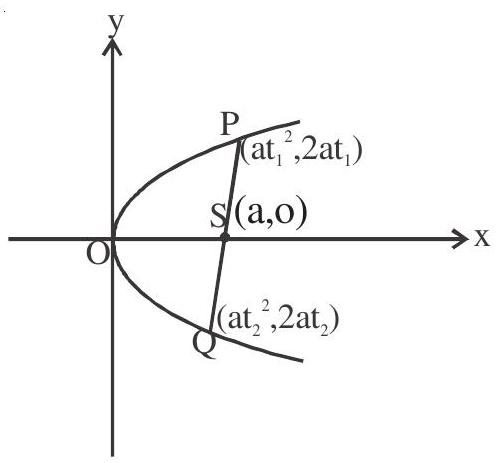
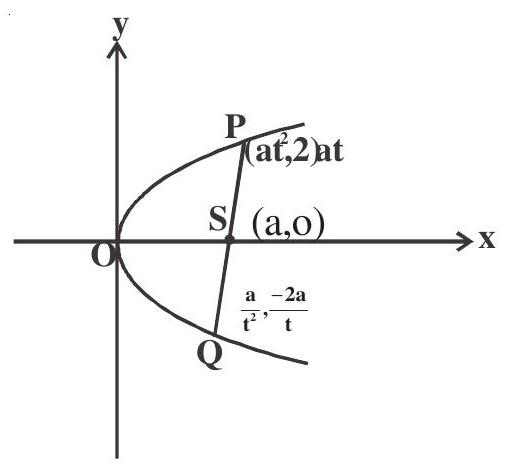
Extremities of a focal chord are $\left(\mathrm{at}^{2}, 2 \mathrm{at}\right)$ and $\frac{\mathrm{a}}{\mathrm{t}^{2}}, \frac{-2 \mathrm{a}}{\mathrm{t}}$.
2. Length of focal chord is a $t+\frac{1}{t}^{2}$
$ \begin{aligned} P Q & =P S+S Q \\ & =a t^{2}+a+\frac{a}{t^{2}}+a \\ & =a t^{2}+\frac{1}{t^{2}}+2 \\ & =a t+\frac{1}{t}^{2} \end{aligned} $
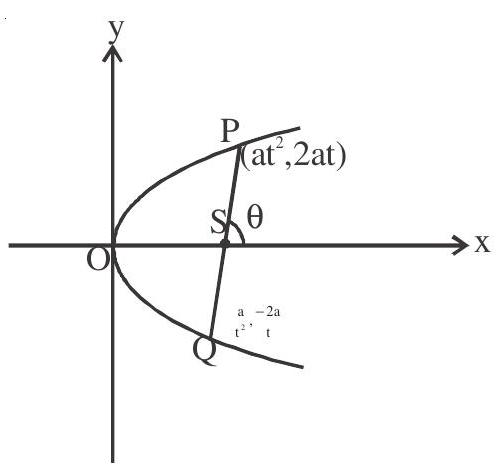
3. The length of the focal chord which makes an angle $\theta$ with the positive direction of $x$-axis is $4 \mathrm{a} \operatorname{cosec}^{2} \theta$.
We know $\mathrm{PQ}=\mathrm{a} \quad \mathrm{t}+\frac{1}{\mathrm{t}}^{2}$
$ \begin{aligned} & \text { slope }=\tan \theta=\frac{2 \mathrm{at}+\frac{2 \mathrm{a}}{\mathrm{t}}}{\mathrm{at}^{2}-\frac{\mathrm{a}}{\mathrm{t}^{2}}} \\ & \text { slope }=\tan \theta=\frac{2}{\mathrm{t}-\frac{1}{\mathrm{t}}} \\ & 2 \cot \theta=\mathrm{t}-\frac{1}{\mathrm{t}} \\ & \therefore \mathrm{PQ}=\mathrm{a} \mathrm{t}+\frac{1}{\mathrm{t}}^{2} \\ & =\mathrm{a} \quad \mathrm{t}-\frac{1}{\mathrm{t}}^{2}+4 \\ & =\mathrm{a}\left[4 \cot ^{2} \theta+4\right] \quad(\mid \operatorname{cosec} \theta \geq 1) \\ & =4 \mathrm{a} \operatorname{cosec}^{2} \theta \quad \end{aligned} $
- Minimum length of $\mathrm{PQ}=4 \mathrm{a} \quad$ (i.e. latus rectum)
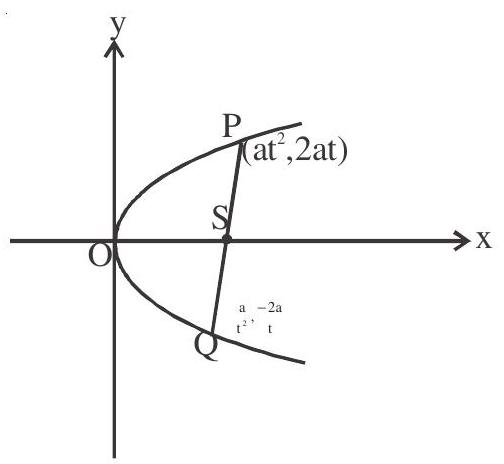
4. Semi latus rectum of a parabola is the harmonic mean between the segments of any focal chord of the parabola.
$ \begin{aligned} & \mathrm{SP}=\mathrm{a}+\mathrm{at}^{2}, \quad \mathrm{SQ}=\mathrm{a}+\frac{\mathrm{a}}{\mathrm{t}^{2}} \\ & \frac{1}{\mathrm{SP}}+\frac{1}{\mathrm{SQ}}=\frac{1}{\mathrm{a}+\mathrm{at}^{2}}+\frac{1}{\mathrm{a}+\frac{\mathrm{a}}{\mathrm{t}^{2}}}=\frac{1}{\mathrm{a}+\mathrm{at^{2 }}}+\frac{\mathrm{t}^{2}}{\mathrm{at}^{2}+\mathrm{a}}=\frac{1}{\mathrm{a}} \\ & \therefore 2 \mathrm{a}=2 x \frac{\mathrm{SP} x \mathrm{SQ}}{\mathrm{SP}+\mathrm{SQ}} \end{aligned} $
Semi latus rectum $=$ Harmonic Mean of SP and SQ.
5. Circle described on the focal length as diameter touches the tangent at vertex.
Equation of circle PS as diameter is
$\left(x-a t^{2}\right)(x-a)+(y-2 a t) y=0$
Equation of $y$-axis is $x=0$
After solving $\mathrm{y}^{2}-2 a t y+\mathrm{a}^{2} \mathrm{t}^{2}=0$
$ (y-a t)^{2}=0 $
$\therefore$ circle touches the $y$-axis at $(0$, at $)$.
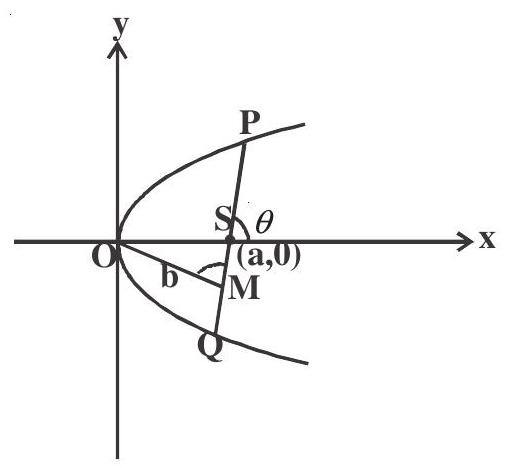
Example: 1 The length of a focal chord of the parabola $y^{2}=4 a x$ at a distance $b$ from the vertex is $\mathrm{c}$, then
(a). $\mathrm{b}^{2}=4 \mathrm{ac}$
(b). $ b^{2} \mathrm{c}=\mathrm{a}^{3}$
(c). $ b^{2} \mathrm{c}=4 \mathrm{a}^{3}$
(d). $ 4 b^{2} c=a^{3}$
Show Answer
Solution: $\mathrm{PQ}=4 \mathrm{a} \operatorname{cosec}^{2} \theta=\mathrm{c}$
In $\triangle \mathrm{OMS}, \sin \theta=\frac{\mathrm{b}}{\mathrm{a}}$
$ \begin{aligned} & \operatorname{cosec}^{2} \theta=\frac{\mathrm{a}^{2}}{\mathrm{~b}^{2}} \\ \therefore & c=4 a \cdot \frac{\mathrm{a}^{2}}{\mathrm{~b}^{2}} b^{2} c=4 \mathrm{a}^{3} \end{aligned} $
Answer: c
Example: 2 The coordinates of the ends of a focal chord of a parabola $y^{2}=4 a x$ are $\left(x _{1}, y _{1}\right)$ and $\left(\mathrm{x} _{2}, \mathrm{y} _{2}\right)$ then value of $\mathrm{x} _{1} \mathrm{x} _{2}+\mathrm{y} _{1} \mathrm{y} _{2}$ is equal to
(a). $ 3 \mathrm{a}^{2}$
(b). $-3 a^{2}$
(c). $\mathrm{a}^{2}$
(d). $-a^{2}$
Show Answer
Solution: Let $\left(\mathrm{at} _{1}^{2}, 2 \mathrm{at} _{1}\right) \equiv\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ and $\left(\mathrm{at} _{2}^{2}, 2 \mathrm{at} _{2}\right) \equiv\left(\mathrm{x} _{2}, \mathrm{y} _{2}\right)$ such that $\mathrm{t} _{1} \mathrm{t} _{2}=-1$
$\therefore \mathrm{x} _{1} \mathrm{x} _{2}+\mathrm{y} _{1} \mathrm{y} _{2}=\mathrm{a}^{2} \mathrm{t} _{1}^{2} \mathrm{t} _{2}^{2}+4 \mathrm{a}^{2} \mathrm{t} _{1} \mathrm{t} _{2}=\mathrm{a}^{2}-4 \mathrm{a}^{2}=-3 \mathrm{a}^{2}$
Answer: b
Practice questions
1. The focus of the parabola $x^{2}+8 x+12 y+4=0$ is
(a). $(4,2)$
(b). $(-2,-4)$
(c). $(2,4)$
(d). $(-4,-2)$
Show Answer
Answer: (d)2. The equation of the parabola with vertex at $(3,2)$ and focus at $(5,2)$ is
(a). $x^{2}-8 x-4 y-28=0$
(b). $y^{2}-8 x-4 y-28=0$
(c). $x^{2}+8 x-4 y-28=0$
(d). $y^{2}+8 x+4 y-28=0$
Show Answer
Answer: (b)3. The equation of the latus rectum of the parabola $x^{2}+4 x+2 y=0$ is
(a). $2 \mathrm{y}-3=0$
(b). $3 \mathrm{y}-2=0$
(c). $2 y+3=0$
(d). $3 y+2=0$
Show Answer
Answer: (a)4. The equation of the parabola whose axis is parallel to $x$-axis and which passes through the points $(0,4),(1,9)$ and $(-2,6)$ is
(a). $\mathrm{y}^{2}+5 \mathrm{x}-25 \mathrm{y}+139=0$
(b). $3 y^{2}+5 x-25 y+52=0$
(c). $2 \mathrm{y}^{2}-5 \mathrm{x}-25 \mathrm{y}+68=0$
(d). none of these
Show Answer
Answer: (c)5. The parametric equation $x=a^{2}+b t+c, y=a^{\prime} t^{2}+b^{\prime} t+c^{\prime}$ represents
(a). a circle
(b). a parabola
(c). an ellipse
(d). none of these





