PARABOLA-4
Line and Parabola:
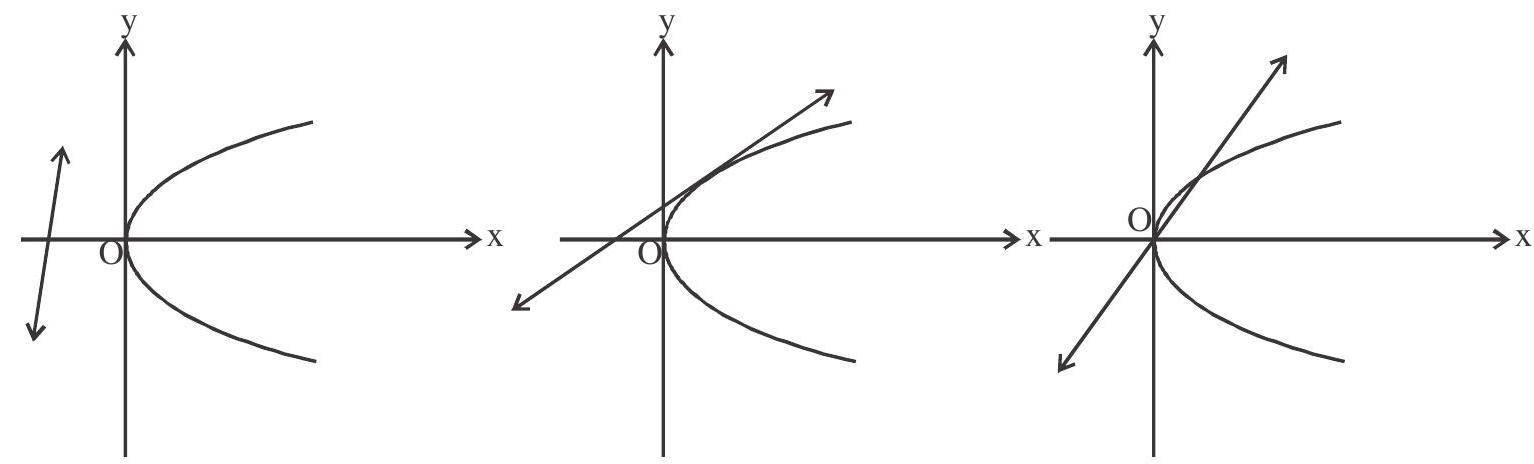
Let equation of line be $y=m x+c$ and equation of parabola be $y^{2}=4 a x$.
$(\mathrm{mx}+\mathrm{c})^{2}=4 \mathrm{ax}$
$\mathrm{m}^{2} \mathrm{x}^{2}+2 \mathrm{x}(\mathrm{mc}-2 \mathrm{a})+\mathrm{c}^{2}=0$
$\mathrm{D}=\{2(\mathrm{mc}-2 \mathrm{a})\}^{2}-4 \cdot \mathrm{m}^{2} \cdot \mathrm{c}^{2}$
$=4\left(4 \mathrm{a}^{2}-4 \mathrm{amc}\right)$
If $\mathrm{D}<0$, line do not intersect parabol(a).
i.e. $\quad \mathrm{a}<\mathrm{mc}$
If $\mathrm{D}=0$ i.e. $\quad \mathrm{a}=\mathrm{mc}$, line touches the parabola (condition of tangency)
If $\mathrm{D}>0$ i.e. $\mathrm{a}>\mathrm{mc}$, line intersect the parabola at two points.
Equation of tangent (Point form)
Equation of parabola $\mathrm{y}^{2}=4 \mathrm{ax}$
Differentiate w.r.t.x
$2y \frac{d y}{d x}=4 a$
slope of tangent $=\frac{2 \mathrm{a}}{\mathrm{y} _{1}}$
Equation of tangent $y-y _{1}=\frac{2 a}{y _{1}}\left(x-x _{1}\right)$
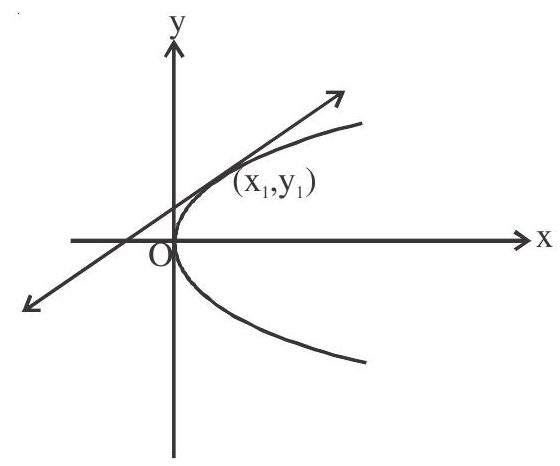
$ \begin{aligned} & \mathrm{y} _{1}-\mathrm{y} _{1}^{2}=2 \mathrm{ax}-2 \mathrm{ax} _{1} \\ & \mathrm{y} _{1}=2 \mathrm{ax}+2 \mathrm{ax} _{1} \\ & \mathrm{y} _{1}=2 \mathrm{a}\left(\mathrm{x}+\mathrm{x} _{1}\right) \end{aligned} $
Equation of tangent (Paramatric form)
$ \begin{aligned} & y \cdot 2 a t=2 a\left(x+a t^{2}\right) \\ & t y=x+a t^{2} \end{aligned} $
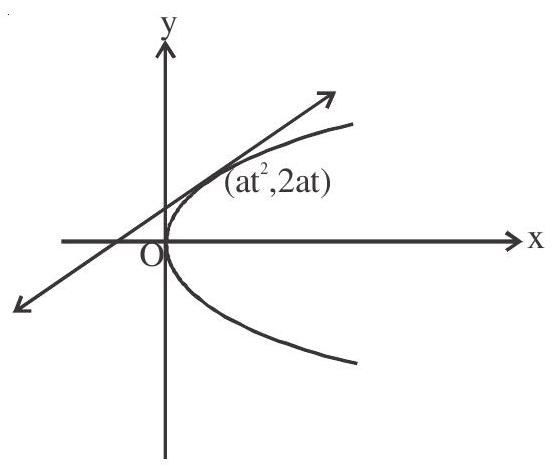
Equation of tangent (slope form)
$ \mathrm{y}=\mathrm{mx}+\frac{\mathrm{a}}{\mathrm{m}} $
Point of contact $\frac{\mathrm{a}}{\mathrm{m}^{2}}, \frac{2 \mathrm{a}}{\mathrm{m}}$
- Equation of tangent to the parabola $(\mathrm{y}-\mathrm{k})^{2}=4 \mathrm{a}(\mathrm{x}-\mathrm{h})$ is
$ \mathrm{y}-\mathrm{k}=\mathrm{m}(\mathrm{x}-\mathrm{h})+\frac{\mathrm{a}}{\mathrm{m}} $
Equation of tangent:
| Parabola | Point form | Pt. of contact | Parametric form | Pt. of contact | slope form | Pt. of contact |
|---|---|---|---|---|---|---|
| $\mathrm{y}^{2}=4 \mathrm{ax}$ | $\mathrm{yy} _{1}=2 \mathrm{a}\left(\mathrm{x}+\mathrm{x} _{1}\right)$ | $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ | $\mathrm{ty}=\mathrm{x}+\mathrm{at}^{2}$ | $\left(\mathrm{at}^{2}, 2 \mathrm{at}\right)$ | $\mathrm{y}=\mathrm{mx}+\frac{\mathrm{a}}{\mathrm{m}}$ | $\frac{\mathrm{a}}{\mathrm{m}^{2}}, \frac{2 \mathrm{a}}{\mathrm{m}}$ |
| $\mathrm{y}^{2}=-4 \mathrm{ax}$ | $\mathrm{yy} _{1}=-2 \mathrm{a}\left(\mathrm{x}+\mathrm{x} _{1}\right) $ | $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ | $\mathrm{ty}=-\mathrm{x}+\mathrm{at}^{2}$ | $\left(-\mathrm{at}^{2}, 2 \mathrm{at}\right)$ | $\mathrm{y}=\mathrm{mx}-\frac{\mathrm{a}}{\mathrm{m}}$ | $-\frac{\mathrm{a}}{\mathrm{m}^{2}}, \frac{-2 \mathrm{a}}{\mathrm{m}}$ |
| $\mathrm{x}^{2}=4 \mathrm{ay}$ | $\mathrm{xx} _{1}=2 \mathrm{a}\left(\mathrm{y}+\mathrm{y} _{1}\right) \quad $ | $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ | $\mathrm{tx}=\mathrm{y}+\mathrm{at}^{2}$ | $\left(2 \mathrm{at}, \mathrm{at}^{2}\right)$ | $\mathrm{x}=\mathrm{my}+\frac{\mathrm{a}}{\mathrm{m}}$ | $\frac{2 \mathrm{a}}{\mathrm{m}}, \frac{\mathrm{a}}{\mathrm{m}^{2}}$ |
| $\mathrm{x}^{2}=-4 \mathrm{ay}$ | $\mathrm{xx} _{1}=-2 \mathrm{a}\left(\mathrm{y}+\mathrm{y} _{1}\right) \quad $ | $\left(\mathrm{x} _{1}, \mathrm{y} _{1}\right)$ | $\mathrm{tx}=-\mathrm{y}+\mathrm{at}^{2}$ | $\left(2 \mathrm{at},-\mathrm{at}^{2}\right)$ | $\mathrm{x}=\mathrm{my}-\frac{\mathrm{a}}{\mathrm{m}} \quad$ | $\frac{-2 \mathrm{a}}{\mathrm{m}}, \frac{-\mathrm{a}}{\mathrm{m}^{2}}$ |
Pair of Tangents from point $\left(x _{1}, y _{1}\right)$
Let eq of parabola be $\quad y^{2}=4 a x$
$S \equiv \mathrm{y}^{2}-4 \mathrm{ax}$
$S _{1} \equiv y _{1}^{2}-4 \mathrm{ax} _{1}$
$\mathrm{T} \equiv \mathrm{yy} _{1}-2 \mathrm{a}\left(\mathrm{x}+\mathrm{x} _{1}\right)$
Equation of pair of tangents is $\mathrm{SS} _{1}=\mathrm{T}^{2} \quad$ i.e.
$\left(y^{2}-4 a x\right)\left(y _{1}^{2}-4 a _{1}\right)=\left\{y _{1}-2 a\left(x+x _{1}\right)\right\}^{2}$
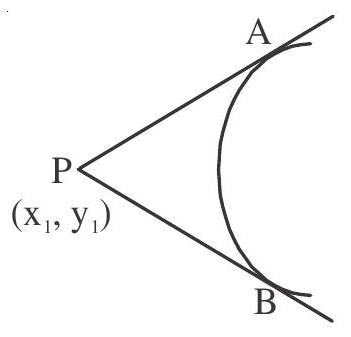
Properties of Tangents:
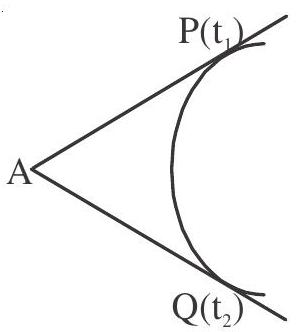
1. Point of intersection of two tangents of the parabola:-
Equation of tangent at $\mathrm{P}$ is $\mathrm{t} _{1} \mathrm{y}=\mathrm{x}+\mathrm{at} _{1}^{2}$
Equation of tangent at $\mathrm{Q}$ is $\mathrm{t} _{2} \mathrm{y}=\mathrm{x}+\mathrm{at} _{2}^{2}$
Solving these equations, we get
$\mathrm{x}=\mathrm{at} _{1} \mathrm{t} _{2}, \quad \mathrm{y}=\mathrm{at} _{1}+\mathrm{at} _{2}$
$\mathrm{A}\left(\mathrm{at} _{1} \mathrm{t} _{2}, \mathrm{a}\left(\mathrm{t} _{1}+\mathrm{t} _{2}\right)\right)$
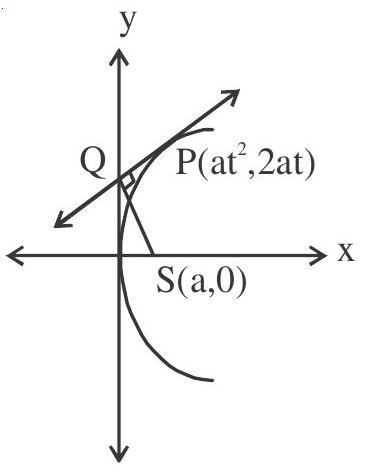
2. Locus of foot of prependicular from focus upon any tangent is tangent at vertex:-
Equation of tangent at $\mathrm{P}$ is ty $=\mathrm{x}+\mathrm{at}^{2}$
Let the tangent meet $\mathrm{y}$-axis at $\mathrm{Q}$ then $\mathrm{Q}(0$, at
$ \begin{aligned} \therefore \quad & \text { slope of } Q S=\frac{-a t}{a}=-t \\ & \text { slope of tangent }=\frac{1}{t} \\ & \frac{1}{t} \times(-t)=-1 \quad S Q \perp \text { tangent } \end{aligned} $
3. Length of tangent between the pt. of contact and the point where tangent meets the directrix subtends right angle at focus:-
Eqation of tangent at $P(t)$
$ t y=x+a t^{2} $
Point of intersection with directrix $x=-a$ is
$ -\mathrm{a}, \mathrm{at}-\frac{\mathrm{a}}{\mathrm{t}} $
slope $\mathrm{SP}=\frac{2 \mathrm{at}}{\mathrm{at}^{2}-\mathrm{a}}=\frac{2 \mathrm{t}}{\mathrm{t}^{2}-1}$
$ \begin{aligned} \text { slope } Q S= & \frac{a t-\frac{a}{t}}{-2 a}=\frac{t^{2}-1}{-2 t} \\ & m _{1} m _{2}=-1 \\ & P S \perp Q S \end{aligned} $
4. Tangent at extremities of focal chord are perpendicular and intersect on directrix
(Locus of intersection point of tangents at extremities of focal chord is directrix)
Let $\mathrm{P}\left(\mathrm{at} \mathrm{t}^{2}\right.$, 2at) and $\mathrm{Q} \frac{\mathrm{a}}{\mathrm{t}^{2}}, \frac{-2 \mathrm{a}}{\mathrm{t}}$
Equation of tangent at $P \quad t y=x+a t^{2}……..(1)$
Equation of tangent at $Q \quad-\frac{1}{t} y=x+\frac{a}{t^{2}}$
$y=-t x-\frac{a}{t} …….(2)$
Point of intersection of both tangents, we get after sloving (1) & (2) i.e.
$ x+a=0 $
A point lies on the directrix.
Practice questions
1. If the tangents to the parabola $y^{2}=4 a x$ at the points $\left(x _{1}, y _{1}\right)$ and $\left(x _{2}, y _{2}\right)$ meet at the point $\left(x _{3}, y _{3}\right)$ then
(a). $\mathrm{y} _{3}^{2}=\sqrt{\mathrm{y} _{1} \mathrm{y} _{2}}$
(b). $2 \mathrm{y} _{3}=\mathrm{y} _{1}+\mathrm{y} _{2}$
(c).
(d). none of these
Show Answer
Answer: (a)2. A right angled triangle $\mathrm{ABC}$ is inscribed in parabola $\mathrm{y}^{2}=4 \mathrm{x}$, where $\mathrm{A}$ is vertex of parabola and $\angle \mathrm{BAC}=90^{\circ}$. If $\mathrm{AB}=$, then area of $\triangle \mathrm{ABC}$ is
(a). 40
(b). 10
(c). 20
(d). $4 \sqrt{5}$
Show Answer
Answer: (c)3. The locus of the point $(\sqrt{3 h}, \sqrt{3 k+2})$ if it lies on the line $x-y-1=0$ is a
(a). circle
(b). parabola
(c). straight line
(d). none of these
Show Answer
Answer: (b)4. The length of the chord of the parabola $y^{2}=x$ which is bisected at the point $(2,1)$ is
(a). 5
(b). 4
(c). $ 2 \sqrt{5}$
(d). $5 \sqrt{2}$
Show Answer
Answer: (c)5. If $y=m x+c$ touches the parabola $y^{2}=4 a(x+a)$, then
(a). $\mathrm{c}=\frac{\mathrm{a}}{\mathrm{m}}$
(b). $ \mathrm{c}=\mathrm{a}+\frac{\mathrm{a}}{\mathrm{m}}$
(c). $ \mathrm{c}=\frac{2 \mathrm{a}}{\mathrm{m}}$
(d). $ \mathrm{c}=\mathrm{am}+\frac{\mathrm{a}}{\mathrm{m}}$
$ \frac{\sqrt{25}}{\mathrm{y} _{3}}=\frac{1}{\mathrm{y} _{1}}+\frac{1}{\mathrm{y} _{2}} $





