Conormal points:

Let $\mathrm{P}(\mathrm{h}, \mathrm{k})$ be a point and equation of parabola be $\mathrm{y}^{2}=4 \mathrm{ax}$.

Equation of normal is

$ y=m x-2 a m-a m^{3} $

If passes through $(\mathrm{h}, \mathrm{k})$ so

$ \begin{aligned} & \mathrm{k}=\mathrm{mh}-2 \mathrm{am}-\mathrm{am}^{3} \\ & \mathrm{am}^{3}+2 \mathrm{am}-\mathrm{mh}+\mathrm{k}=0 \\ & \mathrm{am}^{3}+\mathrm{m}(2 \mathrm{a}-\mathrm{h})+\mathrm{k}=0 \end{aligned} $

Suppose $\mathrm{m} _{1}, \mathrm{~m} _{2}, \mathrm{~m} _{3}$ are the roots of this equation

$\therefore \quad \mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}=0$

$ \begin{aligned} & \mathrm{m} _{1} \mathrm{~m} _{2}+\mathrm{m} _{2} \mathrm{~m} _{3}+\mathrm{m} _{3} \mathrm{~m} _{1}=\frac{2 \mathrm{a}-\mathrm{h}}{\mathrm{a}} \\ & \mathrm{m} _{1} \cdot \mathrm{m} _{2} \cdot \mathrm{m} _{3}=-\frac{\mathrm{k}}{\mathrm{a}} \end{aligned} $

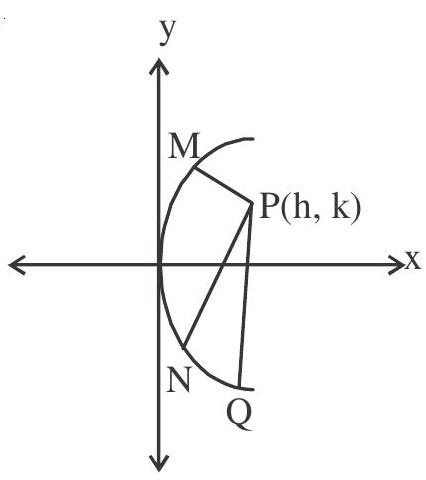
So maximum three normal say PM, PN, PQ drawn through P. Points M, N, Q are called co-normal points.

• The algebraic sum of ordinates of the conormal points is zero. Let the coordinates of conormal points be $\mathrm{M}\left(\mathrm{am} _{1}{ }^{2},-2 \mathrm{am} _{1}\right), \mathrm{N}\left(\mathrm{am} _{2}{ }^{2},-2 \mathrm{am} _{2}\right)$ and $\mathrm{Q}\left(\mathrm{am} _{3}^{2},-2 \mathrm{am} _{3}\right)$. The ordinates of these points $\mathrm{y} _{1}+\mathrm{y} _{2}+\mathrm{y} _{3}=-2 \mathrm{am} _{1}-2 \mathrm{am} _{2}-2 \mathrm{am} _{3}$ $=-2 \mathrm{a}\left(\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}\right)$ $=0$ $ \Rightarrow \mathrm{y} _{1}+\mathrm{y} _{2}+\mathrm{y} _{3}=0$

• Centroid of the triangle formed by conormal points lies on the axis of parabola. Let coordinates of conormal points be $\mathrm{M}\left(\mathrm{x} _{2}, \mathrm{y} _{1}\right), \mathrm{N}\left(\mathrm{x} _{2}, \mathrm{y} _{2}\right) \mathrm{Q}\left(\mathrm{x} _{3}, \mathrm{y} _{3}\right)$ Then centroid is $\left(\frac{\mathrm{x} _{1}+\mathrm{x} _{2}+\mathrm{x} _{3}}{3}, \frac{\mathrm{y} _{1}+\mathrm{y} _{2}+\mathrm{y} _{3}}{3}\right)=\left(\frac{\mathrm{x} _{1}+\mathrm{x} _{2}+\mathrm{x} _{3}}{3}, 0\right)$ Since sum of ordinates is zero. Therefore centroid lies on the axis of parabola.

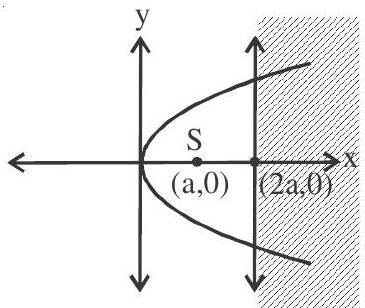
• Normal drawn from a point $\mathrm{P}(\mathrm{h}, \mathrm{k})$ to the parabola are real and distinct if $\mathrm{h}>2 \mathrm{a}$.

$ \begin{aligned} & \mathrm{m} _{1}^{2}+\mathrm{m} _{2}^{2}+\mathrm{m} _{3}^{2}>0 \\ \Rightarrow & \left(\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}\right)^{2}-2\left(\mathrm{~m} _{1} \mathrm{~m} _{2}+\mathrm{m} _{2} \mathrm{~m} _{3}+\mathrm{m} _{1} \mathrm{~m} _{3}\right)>0 \\ \Rightarrow & 0-\frac{2(2 \mathrm{a}-\mathrm{h})}{\mathrm{a}}>0 \\ \Rightarrow & 2 \mathrm{a}-\mathrm{h}<0 \\ \Rightarrow & \mathrm{h}>2 \mathrm{a} \end{aligned} $

This shows that position of point

$(h, k)$ should be in shaded region.

• Equation of a circle passing through the conormal points

Let $\mathrm{M}\left(\mathrm{am} _{1}{ }^{2},-2 \mathrm{am} _{1}\right), \mathrm{N}\left(\mathrm{am} _{2}{ }^{2},-2 \mathrm{am} _{2}\right)$ and $\mathrm{Q}\left(\mathrm{am} _{3}{ }^{2},-2 \mathrm{am} _{3}\right)$ be three points on the parabola $\mathrm{y}^{2}=4ax.$

These three normals passes through point $\mathrm{p}(\mathrm{h}, \mathrm{k})$

$\therefore \mathrm{am}^{3}+(2 \mathrm{a}-\mathrm{h}) \mathrm{m}+\mathrm{k}=0 ……(1)$

$\begin{aligned} \Rightarrow \quad & m_1+m_2+m_3=0 \\ & m_1 m_2+m_2 m_3+m_1 m_3=\frac{2 a-h}{a} \\ & m_1 m_2 m_3=-\frac{k}{a}\end{aligned}$

Let equation of circle be $x^{2}+y^{2}+2 g x+2 f y+c=0$

If the point $\left(\mathrm{am}^{2},-2 \mathrm{am}\right)$ lies on the circle then

$\left(\mathrm{am}^{2}\right)^{2}+(-2 \mathrm{am})^{2}+2 \mathrm{~g}\left(\mathrm{am}^{2}\right)+2 \mathrm{f}(-2 \mathrm{am})+\mathrm{c}=0$

$\mathrm{a}^{2} \mathrm{~m}^{4}+4 \mathrm{a}^{2} \mathrm{~m}^{2}+2 \mathrm{gam}^{2}-4 \mathrm{afm}+\mathrm{c}=0$

$a^{2} m^{4}+\left(4 a^{2} m^{2}+2 g a\right) m^{2}-4 a f m+c=0………(2)$

This equation has four roots say $\mathrm{m} _{1}, \mathrm{~m} _{2}, \mathrm{~m} _{3}, \mathrm{~m} _{4}$ such

that the circle passes through the points $M\left(a m _{1}^{2},-2 \mathrm{am} _{1}\right)$

$\mathrm{N}\left(\mathrm{am} _{2}{ }^{2},-2 \mathrm{am} _{2}\right), \mathrm{Q}\left(\mathrm{am} _{3}{ }^{2},-2 \mathrm{am} _{3}\right)$ and $\mathrm{S}\left(\mathrm{am} _{4}{ }^{2},-2 \mathrm{am} _{4}\right)$

$ \begin{array}{rll} \therefore \mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}+\mathrm{m} _{4} & =0 & \text { (From equation (2)) } \\ 0+\mathrm{m} _{4} & =0 & \text { (Since } \left.\mathrm{m} _{1}+\mathrm{m} _{2}+\mathrm{m} _{3}=0\right) \\ \therefore \quad \mathrm{m} _{4} & =0 \end{array} $

Therefore circle passes through origin.

$ \therefore \mathrm{c}=0 $

Now equation (2) is

$ \begin{aligned} & a^{2} m^{4}+\left(4 a^{2}+2 g a\right) m^{2}-4 a f m=0 \quad(\div a m) \\ & a m^{3}+(4 a+2 g) m-4 f=0 \end{aligned} $

Now this equation is identical with equation (1)

$ \begin{aligned} & \frac{a}{a}=\frac{2 a-h}{4 a+2 g}=\frac{k}{-4 f} \\ & \Rightarrow 2 g=-(2 a+h), 2 f=-\frac{k}{2} \end{aligned} $

Equation of circle is

$ x^{2}+y^{2}-(2 a+h) x-\frac{k}{2} y=0 $