Exercises

1. A tangent PT is drawn at the point $\mathrm{P}(16,16)$ to the parabola $\mathrm{y}^{2}=16 \mathrm{x}$. PT tangent intersect the $\mathrm{x}$-axis at $\mathrm{T}$. If $\mathrm{S}$ be the focus of the parabola, then $\angle \mathrm{TPS}$ is equal to

(a). $\tan ^{-1} \frac{1}{2}$

(b). $\frac{\pi}{4}$

(c). $\frac{1}{2} \tan ^{-1} \frac{1}{2}$

(d). $\tan ^{-1} \frac{3}{4}$

Show Answer

Solution: $\mathrm{ST}=4+\mathrm{AT}=16+4=20$

$\mathrm{PS}=4+16=20$

$\Delta$ TPS is isosceles triangle

$\tan 2 \theta=\frac{16-0}{16-4}=\frac{4}{3}=\frac{2 \tan \theta}{1-\tan ^{2} \theta}$

$2 \tan ^{2} \theta+3 \tan \theta-2=0$

$(2 \tan \theta-1)(\tan \theta+2)=0$

$\tan \theta=\frac{1}{2}, \quad \tan \theta=-2 \quad$ (Not possible)

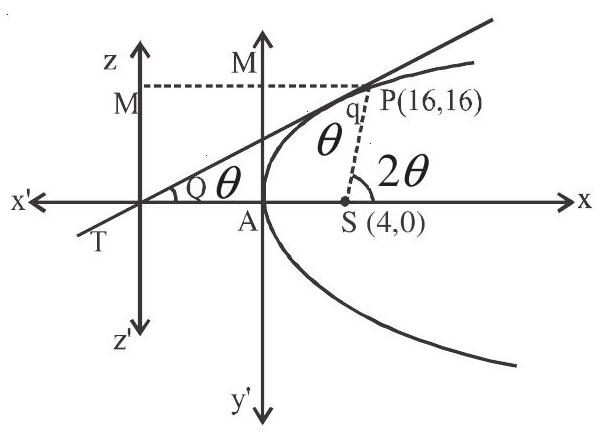
$\theta=\tan ^{-1} \frac{1}{2}\quad$ ( $\theta$ is acute angle)

Answer: a

2. If a, b, $c$ are distinct positive real numbers such that the parabolas $y^{2}=4 a x$ and $y^{2}$ $=4 \mathrm{c}(\mathrm{x}-\mathrm{b})$ will have a common normal, then

(a). $0<\frac{\mathrm{b}}{\mathrm{a}-\mathrm{c}}<1$

(b). $ \frac{b}{a-c}<0$

(c). $ 1<\frac{\mathrm{b}}{\mathrm{a}-\mathrm{c}}<2$

(d). $\frac{b}{a-c}>2$

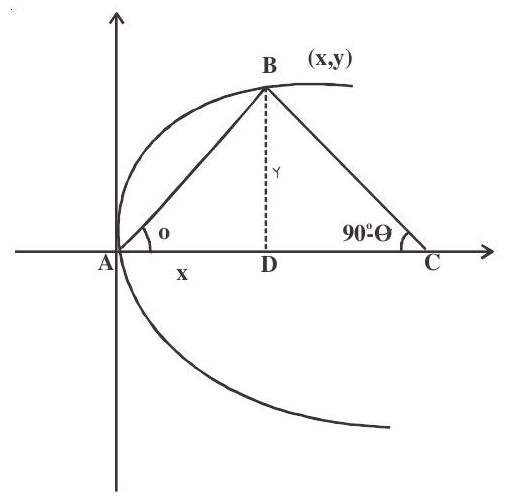
3. If $\mathrm{AB}$ be a chord of the parabola $\mathrm{y}^{2}=4 \mathrm{ax}$ with vertex at $\mathrm{A}$. $\mathrm{BC}$ is perpendicular to $\mathrm{AB}$ such that it meets the axis at $\mathrm{C}$. The projection of the $\mathrm{BC}$ on the axis of parabola is

(a). $2 \mathrm{a}$

(b). $4 \mathrm{a}$

(c). $8 \mathrm{a}$

(d). $16 \mathrm{a}$

Show Answer

Solution: Let coordinates of B be ( $\mathrm{x}, \mathrm{y})$

In $\triangle \mathrm{ABD}, \tan \theta=\frac{\mathrm{BD}}{\mathrm{AD}}=\frac{\mathrm{y}}{\mathrm{x}}$

In $\triangle \mathrm{BCD}, \tan (90-\theta)=\frac{\mathrm{BD}}{\mathrm{DC}}$

$\therefore \mathrm{DC}=\mathrm{y} \cdot \frac{\mathrm{y}}{\mathrm{x}}=\frac{4 \mathrm{ax}}{\mathrm{x}}=4 \mathrm{a}$

Answer: b

4. A circle is descirbed whose centre is the vertex and whose diameter is three-quarters of the latus rectum of the parabola $\mathrm{y}^{2}=4 \mathrm{ax}$. If $\mathrm{PQ}$ is the common-chord of the circle and the parabola and $\mathrm{L} _{1} \mathrm{~L} _{2}$ is the latus rectum, then the area of the trapezium $\mathrm{PL} _{1} \mathrm{~L} _{2} \mathrm{Q}$ is

(a). $\frac{2+\sqrt{2}}{2} a^{2}$

(b). $4 a^{2}$

(c). $2 \sqrt{2}^{2}$

(d). $3 \sqrt{2} \mathrm{a}^{2}$

Show Answer

Solution: Centre of circle $(0,0)$

diameter $=\frac{3}{4} \cdot 4 \mathrm{a}=3 \mathrm{a}$

$\mathrm{Eq}^{\mathrm{n}}$ of circle $\mathrm{x}^{2}+\mathrm{y}^{2}=\frac{9 \mathrm{a}^{2}}{4}…..(1)$

$\mathrm{Eq}^{\mathrm{n}}$ of parabola $\mathrm{y}^{2}=4 \mathrm{ax}……(2)$

coordinates of $\mathrm{P}$ and $\mathrm{Q}$, we get after solving (1) and (2).

$ \begin{aligned} x^{2}+4 a x=\frac{9 a^{2}}{4} & \\ (x+2 a)^{2}=\frac{5 a}{2}^{2} \quad x & =-2 a \pm \frac{5 a}{2} \\ & x=\frac{a}{2}, \frac{-9 a}{2}(\text { not possible }) \end{aligned} $

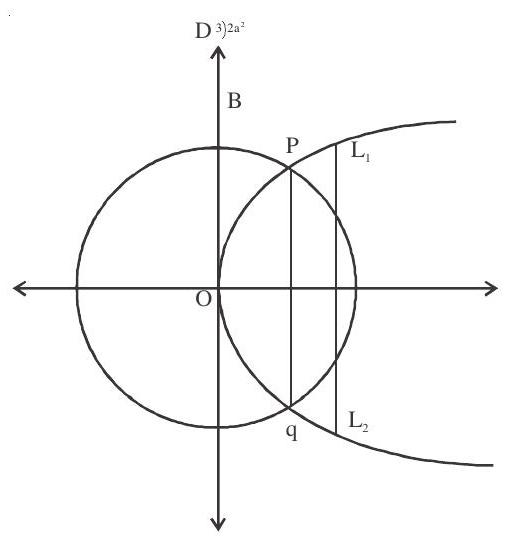$P \frac{a}{2}, \sqrt{2} a, Q \frac{a}{2},-\sqrt{2} a \quad y= \pm \sqrt{2} a$

$\mathrm{PQ}=2 \sqrt{2} \mathrm{a}, \quad \mathrm{L} _{1} \mathrm{~L} _{2}=4 \mathrm{a}$

Area of trapezium $\quad=\frac{1}{2}\left(\mathrm{PQ}+\mathrm{L} _{1} \mathrm{~L} _{2}\right) \mathrm{x}$ distance between them.

$ \begin{aligned} & =\frac{1}{2}(2 \sqrt{2} a+4 a) \times a-\frac{a}{2} \\ & =\frac{(\sqrt{2}+2)}{2} a^{2} \end{aligned} $

Answer: a

5. From the point $(15,12)$ three normals ae drawn to the parabola $y^{2}=4 x$, then centroid of triangle formed by three co-normal points is

(a). $(5,0)$

(b). $(5,4)$

(c). $(9,0)$

(d). $\frac{26}{3}, 0$

6. Aray of light travels along a line $\mathrm{y}=4$ and strikes the surface of a curve $y^{2}=4(x+y)$ then equation of the line along reflected ray travel is

(a). $x+1=0$

(b). $\mathrm{y}-2=0$

(c). $\mathrm{x}=0$

(d). $\mathrm{x}-2=0$

Show Answer

Solution: $y^{2}-4 y=4 x$

$(\mathrm{y}-2)^{2}=4(\mathrm{x}+1)$

Focus $(0,2)$

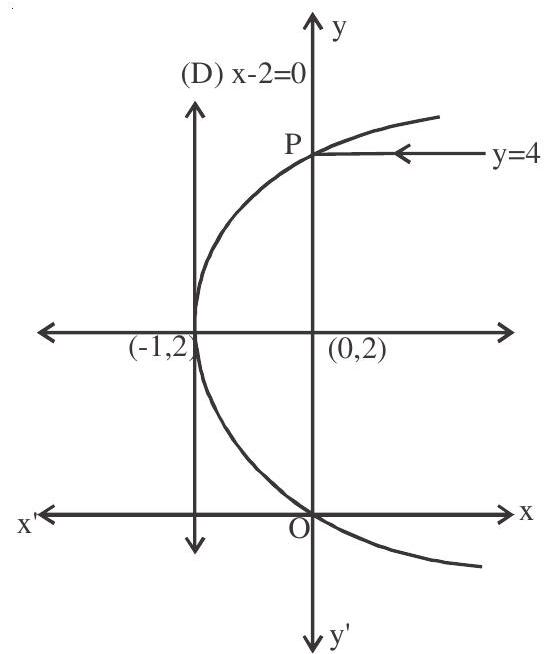
Incident ray is parallel to axis of the parabola, so reflected ray passes through focus $(0,2)$ i.e. $x=0$

Answer: c

7. Let $\mathrm{P}$ be a point of the parabola $\mathrm{y}^{2}=3(2 \mathrm{x}-3)$ and $\mathrm{M}$ is the foot of perpendicular drawn from

Pon the directrix of the parabola, then length of each side of an equilateral triangle SMP, where S is focus of the parabola is

(a). 6

(b). 8

(c). 10

(d). 11

Show Answer

Solution: Equation of parabola is

$\mathrm{y}^{2}=6 \quad \mathrm{x}-\frac{3}{2}$

focus $S(3,0)$

equation of directrix $x=0$

P $\frac{3}{2}+\frac{3}{2} \mathrm{t}^{2}, 3 \mathrm{t}$

Coordinates of $\mathrm{M}(0,3 \mathrm{t})$

$\mathrm{MS}=\sqrt{9+9 \mathrm{t}^{2}}$

$\mathrm{MP}=\frac{3}{2}+\frac{3}{2} \mathrm{t}^{2}$, But MS $=\mathrm{MP}$

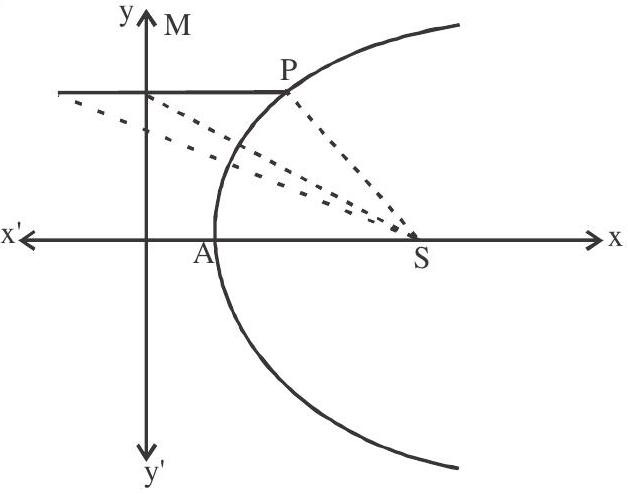
$9+9 \mathrm{t}^{2}=\frac{9}{4}+\frac{9}{4} \mathrm{t}^{2}+\frac{9}{4} \mathrm{t}^{2}$

$\mathrm{t}^{2}=3$

Length of side $=6$

Answer: a

Practice questions

1. The point $(2 a, a)$ lies inside the region bounded by the parabola $x^{2}=4 y$ and its latus rectum. Then

(a). $0<\mathrm{a} \leq 1$

(b). $ 0<\mathrm{a}<1$

(c). $0 \leq \mathrm{a} \leq 1$

(d). $ \mathrm{a}<1$

2. Two perpendicular tangents to $y^{2}=4 a x$ always intersect on the line

(a). $x+a=0$

(b). $\mathrm{x}-\mathrm{a}=0$

(c). $x+2 a=0$

(d). $y+2 a=0$

3. $\mathrm{C} _{1}: \mathrm{y}^{2}=8 \mathrm{x}$ and $\mathrm{C} _{2}: \mathrm{x}^{2}+\mathrm{y}^{2}=2$. Then

(a). $\mathrm{C} _{1}$ and $\mathrm{C} _{2}$ have only two common tangents which are mutually perpendicular

(b). $\mathrm{C} _{1}$ and $\mathrm{C} _{2}$ have two common tangents which are parallel to each other.

(c). does not have any common tangent.

(d). $\mathrm{C} _{1}$ and $\mathrm{C} _{2}$ have four common tangents.

4. Two common tangents to the circle $x^{2}+y^{2}=2 a^{2}$ and $y^{2}=8 a x$ are

(a). $y=(x+a)$

(b). $x= \pm(y+2 a)$

(c). $y= \pm(x+2 a)$

(d). $x= \pm(y+a)$

5. The number of points with integral coordinates that lie in the interior of the circle $x^{2}+y^{2}=16$ and the parabola $\mathrm{y}^{2}=4 \mathrm{x}$ are

(a). 6

(b). 8

(c). 10

(d). 12

6. The vertex of the parabola $x^{2}+y^{2}-2 x y-4 x+4=0$ is at

(a). $\left(-\frac{1}{2},-\frac{1}{2}\right)$

(b). $(-1,-1)$

(c). $(1,1)$

(d). $\left(+\frac{1}{2}, \frac{1}{2}\right)$

7. The length of the latus rectum of the parabola $2\left\{(x-a)^{2}+(y-a)^{2}\right\}=(x+y)^{2}$ is

(a). $\sqrt{2}$ a

(b). $ 2 \mathrm{a}$

(c). $ 2 \sqrt{2}$ a

(d). $3 \sqrt{2} \mathrm{a}$

8. The point on $y^{2}=4 a x$ nearest to the focus is

(a). $(0,0)$

(b). $(\mathrm{a}, 2 \mathrm{a})$

(c). $(a,-2 a)$

(d). $\left(\frac{a}{4}, a\right)$

9. The angle between the tangents drawn from the origin to the parabola $y^{2}=4 a(x-a)$ is

(a). $45^{\circ}$

(b). $60^{\circ}$

(c). $90^{\circ}$

(d). $\tan ^{-1} \frac{1}{2}$

10. The circle $x^{2}+y^{2}+2 \lambda x=0, \lambda \varepsilon R$, touches the parabola $y^{2}=4 x$ externally. Then

(a). $\lambda>0$

(b). $\lambda<0$

(c). $\lambda>1$

(d). none of these