1. Trigonometric equation

An equation involving one or more trigonometrical ratios of unknown angles is called a trigonometrical equation.

2. Solution of trigonometric equation

A value of the unknown angle which satisfies the given equation is called a solution of the equation.

(a). Principal solution. The smallest numerical value, positive or negative for the angle of a trigonometrical equation is called its principal solution. If a positive angle as well as a negative angle of smallest value (and equal) are available, then we take the positive value as the principal values.

(i). The principal solution of $\sin \theta=\mathrm{k},|\mathrm{k}| \leq 1$ is the value of $\theta$ in the interval $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$ which satisfy the equation.

(ii). The principal solution of $\cos \theta=\mathrm{k},|\mathrm{k}| \leq 1$ is the value of $\theta$ in the interval $[0, \pi]$ which satisfy the equation.

(iii). The principal solution of $\tan \theta=\mathrm{k},|\mathrm{k}|<\infty$, the value of $\theta$ in the interval $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$, which satisfy the equation.

(b) General solution. Since all the trigonometric functions are many one onto, therefore, there are infinite values of $\theta$ for which trigonometric functions have the same value. Therefore, all such possible values of $\theta$ for which trigonometric ratios are same is known as general solutions of the variable angle $\theta$.

3. General solutions of trigonometric ratios

$\quad$ (i). If $\sin \theta=0$, then $\theta=n \pi, n \in Z$ (set of integers)

$\quad$ (ii). If $\cos \theta=0$, then $\theta=(2 n+1) \pi / 2, n \in Z$

$\quad$ (iii). If $\tan \theta=0$, then $\theta=n \pi, n \in Z$

$\quad$ (iv). If $\sin \theta=\sin \alpha$ then $\theta=\mathrm{n} \pi+(-1)^{\mathrm{n}} \alpha, \mathrm{n} \in \mathrm{Z}, \alpha \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$

$\quad$ (v). If $\cos \theta=\cos \alpha$, then $\theta=2 \mathrm{n} \pi \pm \alpha, n \in Z, \alpha \in[0, \pi]$

$\quad$ (vi). If $\tan \theta=\tan \alpha$, then $\theta=\mathrm{n} \pi+\alpha, \mathrm{n} \in \mathrm{Z} \alpha \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$

$\quad$ (vii). If $\sin \theta=1$, then $\theta=2 \mathrm{n} \pi+\frac{\pi}{2}, \mathrm{n} \in \mathrm{Z}$

$\quad$ (viii). If $\cos \theta=1$, then $\theta=2 \mathrm{n} \pi, \mathrm{n} \in \mathrm{Z}$

$\quad$ (ix). If $\sin ^{2} \theta=\sin ^{2} \alpha$ or $\cos ^{2} \theta=\cos ^{2} \alpha$ or $\tan ^{2} \theta=\tan ^{2} \alpha$ then $\theta=n \pi \pm \alpha, n \in Z$

$\quad$ (x). If $\sin (a \theta+b)=\sin \alpha$, then $\theta \neq n \pi+(-1)^{n}\left(\frac{a-b}{a}\right)$. First of all we have to write the general solution as such for $\mathrm{a} \theta+\mathrm{b}$ and then, find $\theta$ as $\mathrm{a} \theta+b=n \pi+(-1)^{\mathrm{n}} . \alpha$

$\quad$ $\Rightarrow \theta=\frac{1}{\mathrm{a}}\left[\mathrm{n} \pi+(-1)^{\mathrm{n}} \boldsymbol{\alpha}-\mathrm{b}\right]$

$\quad$ (xi). For $\mathrm{n} \in \mathrm{Z}, \sin \mathrm{n} \pi=0$ and $\cos \mathrm{n} \pi=(-1)^{\mathrm{n}}$

$\quad$ $\sin (\mathrm{n} \pi+\theta)=(-1)^{\mathrm{n}} \sin \theta$

$\quad$ $\cos (\mathrm{n} \pi+\theta)=(-1)^{\mathrm{n}} \cos \theta$

$\quad$ (xii). If $\mathrm{n}$ is an odd integer, then

$\quad$ $\sin \frac{\mathrm{n} \pi}{2}=(-1)^{\frac{\mathrm{n}-1}{2}} \cos \frac{\mathrm{n} \pi}{2}=0$

$\quad$ $\sin \left(\frac{\mathrm{n} \pi}{2}+\theta\right)=(-1)^{\frac{\mathrm{n}-1}{2}} \cos \theta$

$\quad$ $\cos \left(\frac{\mathrm{n} \pi}{2}+\theta\right)=(-1)^{\frac{\mathrm{n}+1}{2}} \sin \theta$

4. Important points to remember

$\quad$ (i). For equations of the type $\sin \theta=\mathrm{k}$ or $\cos \theta=\mathrm{k}$, one must check that $|\mathrm{k}| \leq 1$.

$\quad$ (ii). Avoid squaring the equation, if possible, because it may lead to extraneous solutions.

$\quad$ (iii). Do not cancel the common variable factor from the two sides of the equations which are in a product because we may loose some solutions.

$\quad$ (iv). The answer should not contain such values of $\theta$ which make any of the terms undefined or infinite.

$\quad$ (v). Check that denominator is not zero at any stage while solving equations.

$\quad$ (vi). (a). If $\tan \theta$ or $\sec \theta$ is involved in the equation, $\theta$ should not be odd multiple of $\frac{\pi}{2}$.

$\quad$(b). If $\cot \theta$ or $\operatorname{cosec} \theta$ is involved in the equation, $\theta$ should not be a multiple of $\pi$ or 0 .

$\quad$(vii). If two different trigonometric ratios, such as, $\tan \theta$ and $\sec \theta$ are involved then after solving we cannot apply the usual formulae for general solution, because periodicity of the functions are not same.

$\quad$(viii). If L.H.S. of the given trigonometric equation is always less than or equal to $\mathrm{k}$ and RHS is always greater than $\mathrm{k}$, then no solution exists. If both the sides are equal to $\mathrm{k}$ for same value of $\theta$, then solution exists and if they are equal for different value of $\theta$, then solution does not exist.

Examples

1. The general solution of the equation $\sum \cos \left(\mathrm{r}^{2} \mathrm{x}\right) \sin (\mathrm{rx})=\frac{1}{2}$ is

(a). $2 \mathrm{~m} \pi+\frac{\pi}{6}, \mathrm{~m} \in \mathrm{I}$

(b). $\frac{(4 \mathrm{~m}+1)}{\mathrm{n}(\mathrm{n}+1)} \frac{\pi}{2} \mathrm{~m} \in \mathrm{I}$

(c). $\frac{(4 \mathrm{~m}-1)}{\mathrm{n}(\mathrm{n}+1)} \frac{\pi}{2}, \mathrm{~m} \in \mathrm{I}$

(d). None of these

2. If $[\sin x]+[\sqrt{2} \cos x]=-3, x \in[0,2 \pi][[.]$ denotes the greatest integer function $]$, then $x$ belongs to

(a). $\left(\pi, \frac{5 \pi}{4}\right)$

(b). $\left[\pi, \frac{5 \pi}{4}\right]$

(c). $\left(\frac{5 \pi}{4}, 2 \pi\right)$

(d). $\left[\frac{5 \pi}{4}, 2 \pi\right]$

3. The number of solutions of the equation $\sin x+2 \sin 2 x=3+\sin 3 x$ in the interval $[0, \pi]$ is

(a). 0

(b). 1

(c). 2

(d). 3

4. The number of values of $\theta$ in the interval $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$ suggesting the equation $(\sqrt{3})^{\sec ^{2} \theta}=\tan ^{4} \theta+2 \tan ^{2} \theta$ is

(a). 1

(b). 2

(c). 3

(d). None of these

Show Answer

Solution:

We have

$ \begin{aligned} (\sqrt{3})^{\sec ^{2} \theta} & =\tan ^{4} \theta+2 \tan ^{2} \theta \\ & =\left(1+\tan ^{2} \theta\right)^{2}-1 \\ & =\left(\sec ^{2} \theta\right)^{2}-1 \end{aligned} $

let $\sec ^{2} \theta=\mathrm{x} \therefore \mathrm{x} \geq 1$

$(\sqrt{3})^{x}=x^{2}-1$

graph of $y=(\sqrt{3})^{x} \& y=x^{2}-1$

intersect at one point

When $\mathrm{x}=2 ; \mathrm{y}=3$

$ \therefore \sec ^{2} \theta=2 $

$ \sec \theta= \pm \sqrt{2} $

$\therefore \theta$ takes two values in $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$

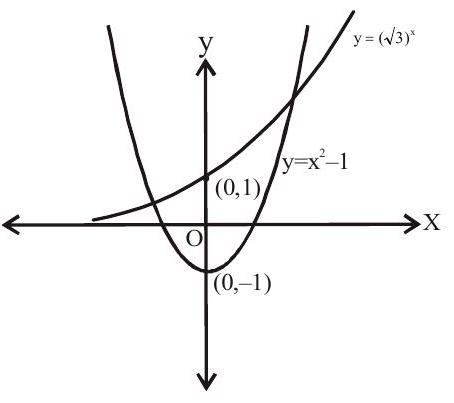
Option ‘b’ is correct

5. If $0 \leq x \leq \pi$ and $81^{\sin ^{2} x}+81^{\cos ^{2} x}=30$ then $x$ is equal to

(a). $\frac{\pi}{6}$

(b). $\frac{\pi}{2}$

(c). $\pi$

(d). $\frac{\pi}{4}$

6. The equation a $\sin x+b \cos x=c$

where $|c|>\sqrt{a^{2}+b^{2}}$ has

(a). one solution

(b). two

(c). no solution

(d). infinite number of solution

Practice questions

1. If $\cos 2 \theta=(\sqrt{2+1})\left(\cos \theta \frac{1}{\sqrt{2}}\right)$, then $\theta=$

(a). $2 \mathrm{n} \pi$

(b). $2 \mathrm{n} \pi \pm \frac{\pi}{4}$

(c). $2 \mathrm{n} \pi \pm \frac{\pi}{3}$

(d). none

2. It $3 \cos ^{2} \theta-2 \sqrt{3} \sin \theta \cos \theta-3 \sin ^{2} \theta=0$ then $\theta$ equals

(a). $\frac{n \pi}{2}+\frac{\pi}{6}$

(b). $\frac{n \pi}{2}-\frac{\pi}{6}$

(c). $\frac{n \pi}{2}+\frac{\pi}{3}$

(d). $\frac{n \pi}{2}-\frac{\pi}{3}$

3. The general solution of $\sin x-3 \sin 2 x+\sin 3 x=\cos x-3 \cos 2 x+\cos 3 x$ is

(a). $\mathrm{n} \pi+\frac{\pi}{8}$

(b). $\frac{n \pi}{2}+\frac{\pi}{8}$

(c). $(-1)^{\mathrm{n}}\left(\frac{\mathrm{n} \pi}{2}\right)+\frac{\pi}{8}$

(d). $2 \mathrm{n} \pi+\cot ^{-1}\left(\frac{3}{2}\right)$

4. The number of points of intersection of $2 y=1$ and $y=\cos x$ in $\frac{-\pi}{2} \leq x \leq \frac{\pi}{2}$ is

(a). 1

(b). 2

(c). 3

(d). 4

5. The number of values of $x$ in the internal $[0,5 \pi]$ satisfying the equation $3 \sin ^{2} x-7 \sin x+2$ $=0$ is

(a). 0

(b). 5

(c). 6

(d). 10

6. The sum of all the solutions of the equation $\cos \theta \cos \left(\frac{\pi}{3}+\theta\right) \cos \left(\frac{\pi}{3}-\theta\right)=\frac{1}{4}, \theta \in[0,6 \pi]$ is

(a). $15 \pi$

(b). $30 \pi$

(c). $\frac{100 \pi}{3}$

(d). none

7. The number of values of $\theta \in[0,4 \pi]$ satisfying the equation $|\sqrt{3} \cos x-\sin x| \geq 2$ is

(a). 0

(b). 2

(c). 4

(d). 8

8. If $\frac{1}{6} \sin \theta, \cos \theta, \tan \theta$ are in G.P., then $\theta$ equals

(a). $2 \mathrm{n} \pi \pm \frac{\pi}{3}$

(b). $2 \mathrm{n} \pi \pm \frac{\pi}{6}$

(c). $ n \pi+(-1)^{n} \frac{\pi}{3}$

(d). $n \pi+\frac{\pi}{3}$

9. The number of solutions of the equation $\tan x+\sec x=2 \cos x$ lying in the internal $[0,2 \pi]$ is

(a). 0

(b). 1

(c). 2

(d). 3

10. The general solution of equation $\sin ^{2} \theta \sec \theta+\sqrt{3} \tan \theta=0$ is

(a). $ \theta=\mathrm{n} \pi+(-1)^{\mathrm{n}+1} \frac{\pi}{3}$

(b). $ \theta=\mathrm{n} \pi$

(c). $ \theta=\mathrm{n} \pi+(-1)^{\mathrm{n}+1} \frac{\pi}{6}$

(d). $\theta=\frac{\mathrm{n} \pi}{2}$

11. Passage

Solution of equations asin $x \pm b \cos x=c$.

General value satisfying two equations. $a \cos \theta \pm \mathrm{b} \sin \theta=\mathrm{c}, \theta$ satisfying two equations.

(a). The equation acos $\theta \pm \mathrm{b} \sin \theta=\mathrm{c}$ be first converted to $\mathrm{r} \cos (\theta \pm \alpha)=\mathrm{c}$ where $\mathrm{a}=\mathrm{r\cos} \alpha, \mathrm{b}=\mathrm{r\sin} \alpha$

(b). $\theta$ satisfying two equations

Find the common value of $\theta$ lying between 0 and $2 \pi$ and then add $2 n \pi$

Answer the following questions based upon above passage

(i). The number of intergral values of $k$ for which the equation $7 \cos x+5 \sin x=2 k+1$ has a solution is

(a). 4

(b). 8

(c). 10

(d). 12

(ii). If $\cos 3 x+\sin \left(2 x-\frac{7 \pi}{6}\right)=-2$ then $x$ equals

(a). $\frac{\pi}{3}(6 m-1)$

(b). $\frac{\pi}{3}(6 m+1)$

(c). $ \frac{\pi}{3}(2 \mathrm{~m}+1)$

(d). none

(iii). The values of $\mathrm{x}$ such that $-\pi<\mathrm{x}<\pi$ and satisfying the equation are given by $8^{\left[1+\left|\cos x^{x}+\cos ^{2} x+\cos ^{3} x\right|+\ldots+\operatorname{tos}\right]}=4^{3} x$ equals

(a). $\frac{\pi}{3}$

(b). $\frac{2 \pi}{3}$

(c). $\frac{-\pi}{3}$

(d). $\frac{-2 \pi}{3}$

(iv). The number of solution of the equaiton $\mathrm{e}^{\sin x}-\mathrm{e}^{-\sin x}-4=0$ is

(a). 1

(b). 2

(c). 4

(d). 0