TRIGONOMETRY FUNCTIONS - 1 (Inverse Trigonometric Functions)
A $f$ unction $f: \mathrm{A} \rightarrow \mathrm{B}$ is invertible if $f$ it is a bijection. The inverse of $f$ is denoted by $f^{-1}$ and is defined as $f^{-1}(\mathrm{y})=\mathrm{x} \Leftrightarrow f(\mathrm{x})=\mathrm{y}$. Trigonometric functions are periodic and hence they are not bijective. But if we restrict their domains and codomains they can be made bijective and we can obtain their inverses.
1. $\operatorname{Sin}^{-1} \mathbf{x}$ :
The symbol $\sin ^{-1} \mathrm{x}$ or $\arcsin \mathrm{x}$ denote the angle $\theta$ so that $\sin \theta=\mathrm{x}$. As a direct meaning, $\sin ^{-1} \mathrm{x}$ is not a function, as it does not satisfy the requirements for a rule to become a function. But by a suitable choice $[-1,1]$ as its domain and standardized set $[-\pi / 2, \pi / 2]$ as its range, then rule $\sin ^{-}$ ${ }^{1} x$ is a single valued function
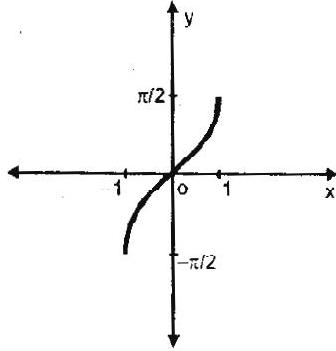
Thus $\sin ^{-1} \mathrm{x}$ is considered as a function with domain $[-1,1]$ and range $[-\pi / 2, \pi / 2]$
The graph of $y=\sin ^{-1} x$ is as shown below which is obtained by taking the mirror image, of the portion of the graph of $y=\sin x$ from $x=-\pi / 2$ to $x=\pi / 2$, on the line $y=x$
2. $\cos ^{-1} \mathbf{x}$ :
By following the discussions, similar to above, we have $\cos ^{-1} \mathrm{x}$ or arccos $\mathrm{x}$ as a function with domain $[-1,1]$ and range $[0, \pi]$
The graph of $y=\cos ^{-1} x$ is similarly obtained as the mirror image of the portion of the graph of $y=$ $\cos \mathrm{x}$ from $\mathrm{x}=0$ to $\mathrm{x}=\pi$

3. $\tan ^{-1} \mathbf{x}:$
We get $\tan ^{-1} x$ or arctan $x$ as a function with domain $R$ and range $(-\pi / 2, \pi / 2)$. Graph of $y=\tan ^{-1} x$

4. $\operatorname{cosec}^{-1} x:$
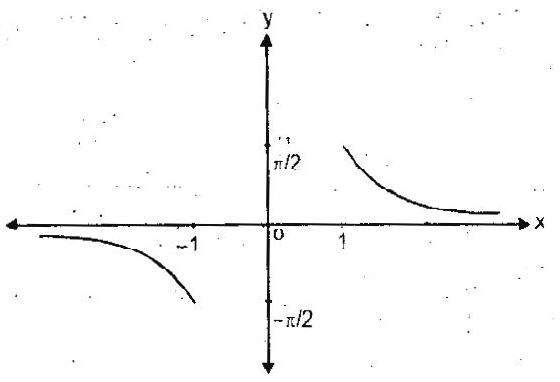
$\operatorname{cosec}^{-1} \mathrm{x}$ or arccosec $\mathrm{x}$ is a function with domain $\mathrm{R}-(-1,1)$ and range $[-\pi / 2, \pi / 2]-\{0\}$. Graph of $y=\operatorname{cosec}^{-1} \mathrm{x}$
5. $\sec ^{-1} \mathbf{x}$ :
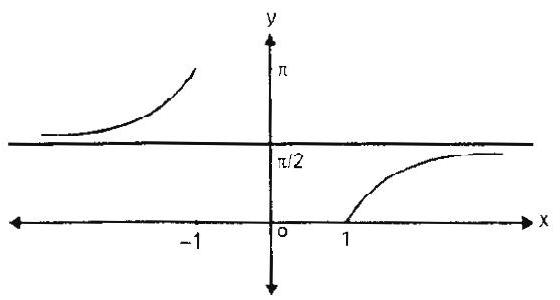
$\sec ^{-1} x$ or arcsec $x$ is a function with domain $R-(-1,1)$ and range $[0, \pi]-\{\pi / 2\}$. Graph of $y=\sec -$ ${ }^{1} x$ is
6. $\cot ^{-1} \mathbf{x}$ :
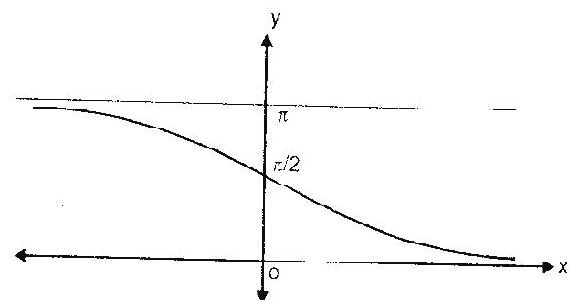
$\cot ^{-1} \mathrm{x}$ or arccot $\mathrm{x}$ is a function with domain $\mathrm{R}$ and range $(0, \pi)$. Graph of $\mathrm{y}=\cot ^{-1} \mathrm{x}$ is
Property : $“-x"$
The graphs of $\sin ^{-1} x, \tan ^{-1} x, \operatorname{cosec}^{-1} x$ are symmetric about origin.
Hence we get
$ \begin{aligned} & \sin ^{-1}(-x)=-\sin ^{-1} x \\ & \tan ^{-1}(-x)=-\tan ^{-1} x \\ & \operatorname{cosec}^{-1}(-x)=-\operatorname{cosec}^{-1} x \end{aligned} $
Also the graphs of $\cos ^{-1} x, \sec ^{-1} x, \cot ^{-1} x$ are symmetric about the point $(0, \pi / 2)$. From this, we get
$ \begin{aligned} & \cos ^{-1}(-\mathrm{x})=\pi _{-}-\cos ^{-1} \mathrm{x} \\ & \sec ^{-1}(-\mathrm{x})=\pi _{-\sec ^{-1} \mathrm{x}} \\ & \cot ^{-1}(-\mathrm{x})=\pi _{-} \cot ^{-1} \mathrm{x} \end{aligned} $
Notes :
(i). $\mathrm{x}^{2}+\mathrm{y}^{2} \leq 1 \& \mathrm{x}, \mathrm{y} \geq 0 \Rightarrow \leq \sin ^{-1} \mathrm{x}+\sin ^{-1} \mathrm{y} \leq \frac{\pi}{2}$ and $\mathrm{x}^{2}+\mathrm{y}^{2} \geq 1$ \& $\mathrm{x}, \mathrm{y} \geq 0$
$ \Rightarrow \frac{\pi}{2} \leq \sin ^{-1} x+\sin ^{-1} y \leq \pi $
(ii). $x y<1$ and $x, y \geq 0 \Rightarrow 0 \leq \tan ^{-1} x+\tan ^{-1} y<\frac{\pi}{2}$; $x y>1$ and $x, y \geq 0 \Rightarrow \frac{\pi}{2}<\tan ^{-1} x+\tan ^{-1} y<\pi$
(iii). For $\mathrm{x}<0$ or $\mathrm{y}<0$ these identities can be used with the help of property " $-\mathrm{x}$ " i.e. change $x$ or $y$ to $-x$ or $-y$ which are positive
Domain & range of inverse trigonometric Functions
| Function | Domain | Range (Principal value branch) |
|---|---|---|
| $\sin ^{-1} \mathrm{x}$ | $[-1, 1]$ | $[-\pi / 2,-\pi / 2]$ |
| $\cos ^{-1} x$ | $[-1, 1]$ | $[0, \pi]$ |
| $\tan ^{-1} x$ | $(-\infty, \infty)$ | $(-\pi / 2, \pi / 2)$ |
| $\cot ^{-1} \mathrm{x}$ | $(-\infty, \infty)$ | $(0, \pi)$ |
| $\operatorname{cosec}^{-1} x$ | $(-\infty,-1] \cup[1, \infty)$ | $[-\pi / 2,0) \cup(0, \pi / 2]$ |
| $\sec ^{-1} \mathrm{x}$ | $(-\infty,-1] \cup[1, \infty)$ | $[0, \pi / 2) \cup(\pi / 2, \pi]$ |
Note: If no branch of an inverse trigonometric function is mentioned, then it means the principal value branch of the function.
Properties of Inverse Trigonometric Functions
1. (i). $\sin ^{-1}(\sin \mathrm{x})=\left\{\begin{array}{l}-2 \mathrm{n} \pi+\mathrm{x}, \quad 2 \mathrm{n} \pi-\frac{\pi}{2} \leq \mathrm{x} \leq 2 \mathrm{n} \pi+\frac{\pi}{2}, \mathrm{n} \in \mathrm{Z} \\ (2 \mathrm{n}+1) \pi-\mathrm{x},(2 \mathrm{n}+1) \pi-\frac{\pi}{2} \leq \mathrm{x} \leq(2 \mathrm{n}+1) \pi+\frac{\pi}{2}, \mathrm{n} \in \mathrm{Z}\end{array}\right.$
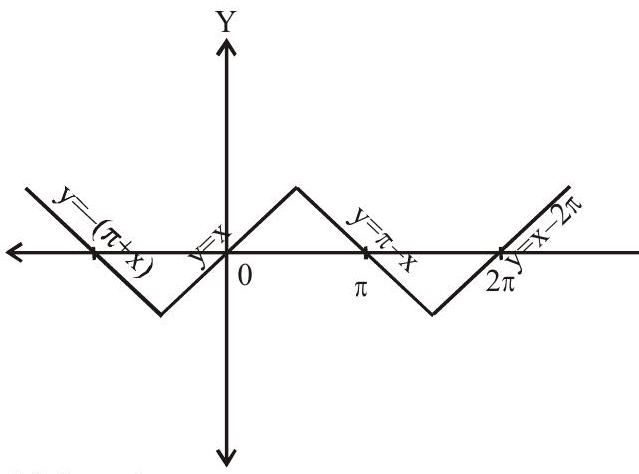
Period $=2 \pi \&$ it is an odd function.
(ii). $\cos ^{-1}(\cos x)=\left\{\begin{array}{l}-2 \mathrm{n} \pi+x, \quad 2 \mathrm{n} \pi \leq \mathrm{x} \leq(2 \mathrm{n}+1) \pi, \quad \mathrm{n} \in \mathrm{Z} \\2\mathrm{n} \pi-x,(2 \mathrm{n}-1) \pi \leq \mathrm{x} \leq 2 \mathrm{n} \pi, \quad \mathrm{n} \in \mathrm{Z} \end{array}\right.$
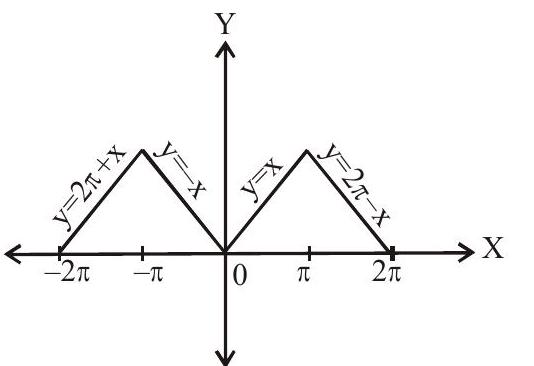
Period $=2 \pi$ and it is an even function
(iii). $\tan ^{-1}(\tan \mathrm{x})=-\mathrm{n} \pi+\mathrm{x}, \mathrm{n} \pi-\frac{\pi}{2}<\mathrm{x}<\mathrm{n} \pi+\frac{\pi}{2}, \mathrm{n} \in \mathrm{Z}$
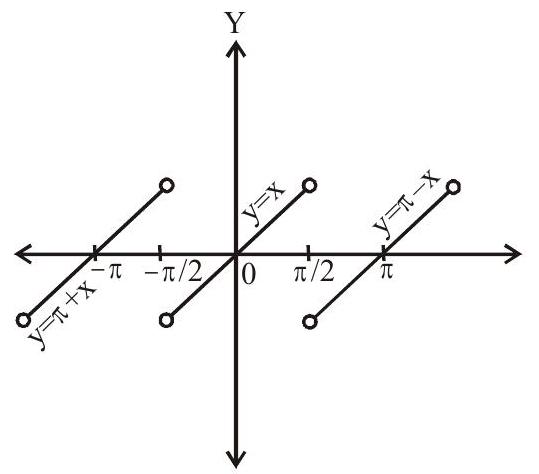
Period $=\pi$
(iv). $\cot ^{-1}(\operatorname{cotx})=-\mathrm{n} \pi+\mathrm{x}, \mathrm{n} \pi<\mathrm{x}<(\mathrm{n}+1) \pi, \mathrm{n} \in \mathrm{Z}$
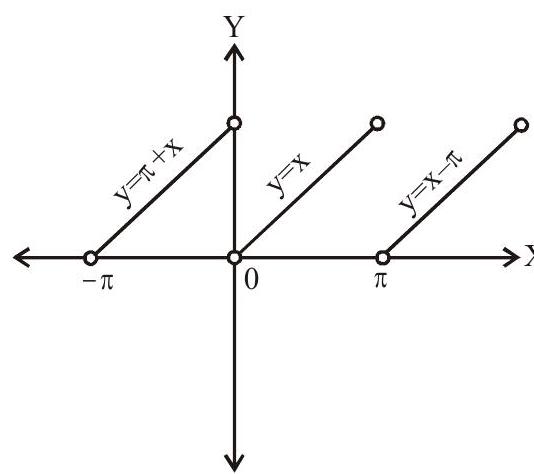
Period $=\pi$
(v). $ \sec ^{-1}(\sec x)=\left\{\begin{array}{l}x-2 n \pi, 2 n \pi \leq x \leq(2 n+1) \pi, x \neq 2 \pi+\frac{\pi}{2} \\ -x+2 n \pi,(2 n-1) \pi \leq x \leq 2 n \pi, x \neq\left(2 n \pi-\frac{\pi}{2} , n \in Z\right.\end{array}\right.$
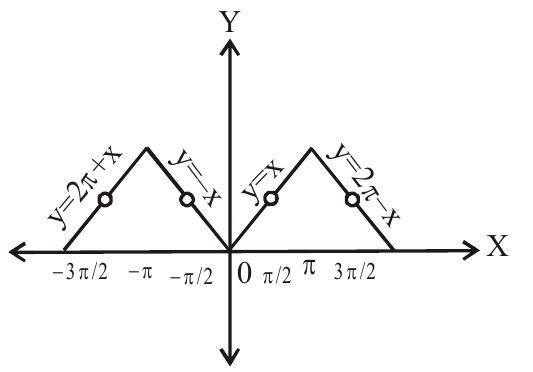
Period $=2 \pi$
(vi). $\operatorname{cosec}^{-1}(\operatorname{cosec} x)=\left\{\begin{array}{l}-2 n \pi+x, 2 n \pi-\frac{\pi}{2} \leq x \leq 2 n \pi+\frac{\pi}{2} \\ (2 n+1) \pi-x,(2 n+1) \pi-\frac{\pi}{2} \leq x \leq(2 n+1) \pi+\frac{\pi}{2}, x \neq n \pi, n \in Z\end{array}\right.$
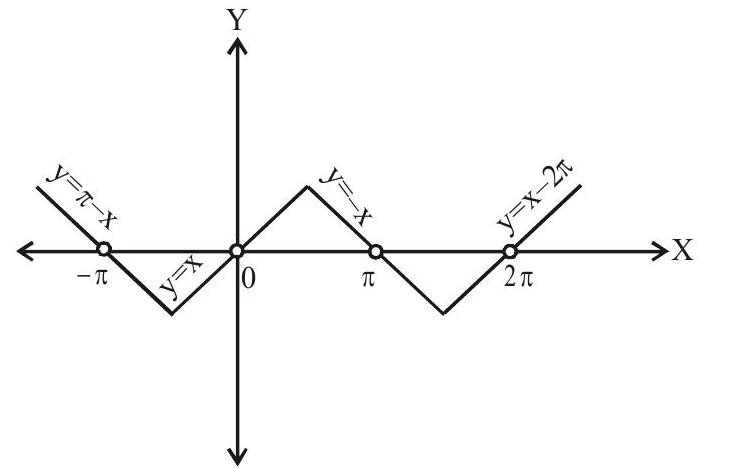
Period $=2 \pi$
2. (i). $\sin \left(\sin ^{-1} x\right)=x,-1 \leq x \leq 1$ $\hspace{1cm}$(ii). $ \cos \left(\cos ^{-1} \mathrm{x}\right)=\mathrm{x},-1 \leq \mathrm{x} \leq 1$
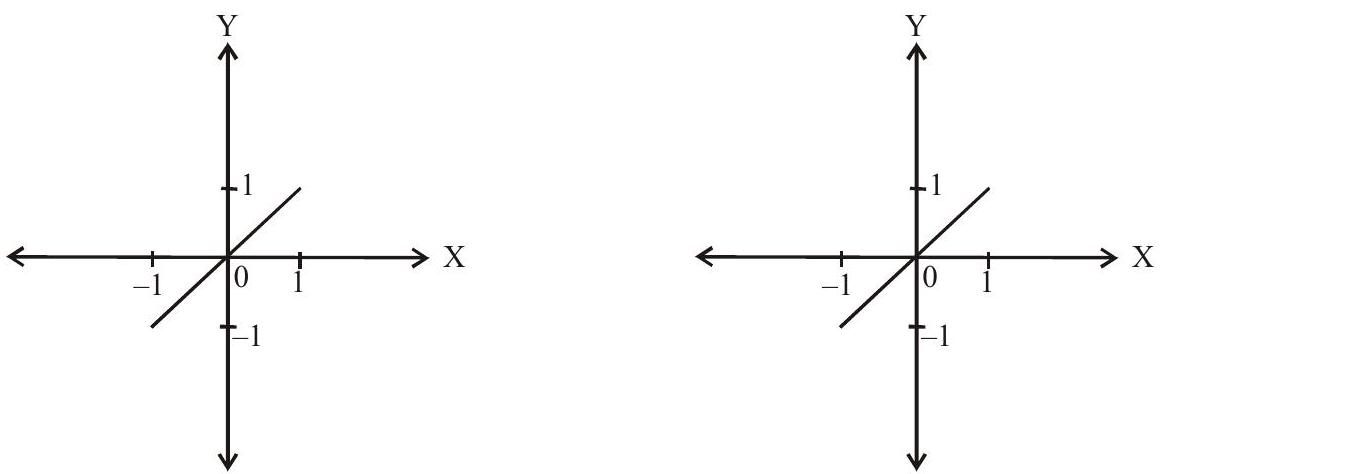
(iii). $\tan \left(\tan ^{-1} x\right)=x, x \in R$ $\hspace{1cm}$(iv). $\cot \left(\cot ^{-1} \mathrm{x}\right)=\mathrm{x}, \mathrm{x} \in \mathrm{R}$
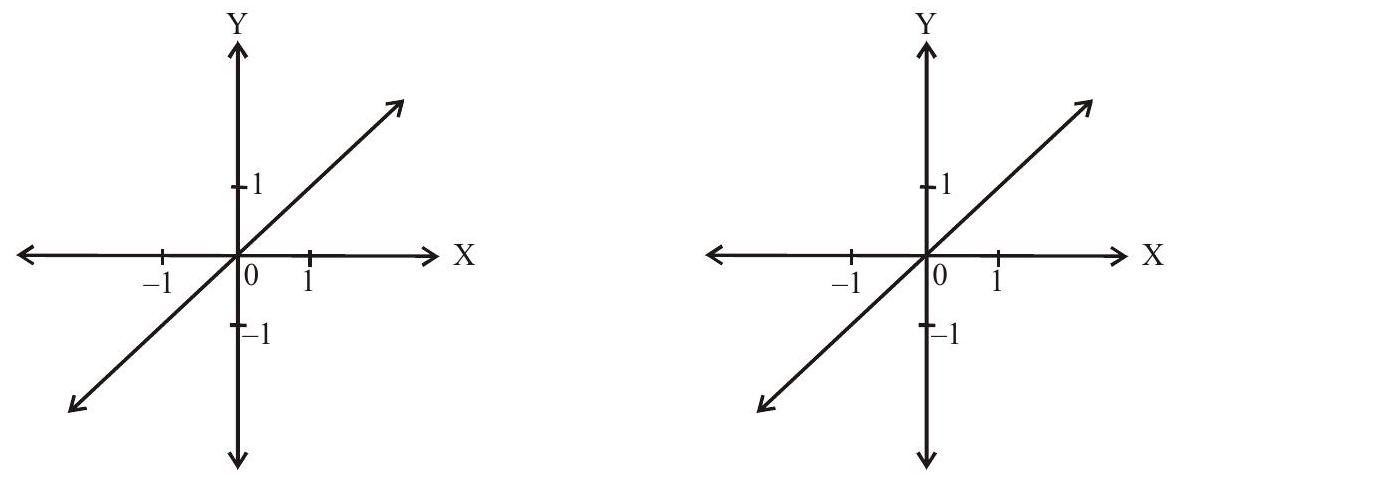
(v). $\sec \left(\sec ^{-1} x\right)=x, x \in R(-\infty,-1] \cup[1, \infty)$
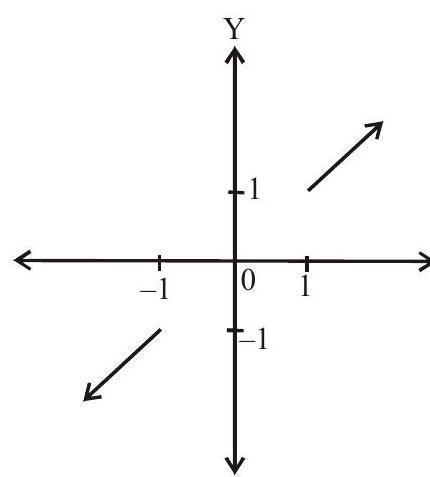
(vi). $\operatorname{cosce}\left(\operatorname{cosce}^{-1} x\right)=x, x \in R(-\infty,-1] \cup[1, \infty)$
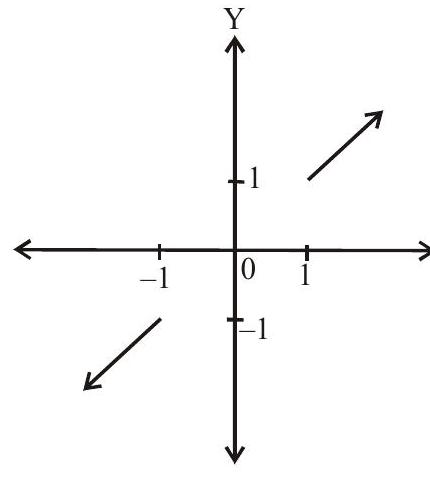
3. (i). $\sin ^{-1} x+\cos ^{-1} x=\pi / 2,-1 \leq x \leq 1$
(ii). $\tan ^{-1} x+\cot ^{-1} x=\pi / 2, x \in R$
(iii).$\sec ^{-1} \mathrm{x}+\operatorname{cosce}^{-1} \mathrm{x}=\pi / 2, \mathrm{x} \in \mathrm{R}(-\infty,-1] \cup[1, \infty)$
4. (i). $\sin ^{-1} x=\operatorname{cosec}^{-1} \frac{1}{x},-1 \leq x \leq 1$
(ii). $\cos ^{-1} x=\sec ^{-1}\left(\frac{1}{x}\right),-1 \leq x \leq 1$
(iii). $\tan ^{-1} x=\left\{\begin{array}{l}\cot ^{-1}(1 / x), x>0 \\ -\pi+\cot ^{-1}(1 / x), x<0\end{array}\right.$
5. (i). $\sin ^{-1}(-x)=-\sin ^{-1} x, \quad-1 \leq x \leq 1$
(ii). $\cos ^{-1}(-x)=\pi-\cos ^{-1} x, \quad-1 \leq x \leq 1$
(iii). $\tan ^{-1}(-x)=-\tan ^{-1} x, \quad-\infty<x<\infty$
(iv). $\cot ^{-1}(-x)=\pi-\cot ^{-1} x, \quad-\infty<x<\infty$
(v). $\operatorname{cosec}^{-1}(-x)=-\operatorname{cosec}^{-1} x, \quad x \leq-1$ or $x \geq 1$
(vi). $\sec ^{-1}(-x)=\pi-\sec ^{-1} x, \quad x \leq-1$ or $x \geq 1$
6. Conversions of inverse trigonometric functions

$ \begin{aligned} \sin ^{-1} x & =\cos ^{-1} \sqrt{1-x^{2}}=\tan ^{-1} \frac{x}{\sqrt{1-x^{2}}} \\ & =\cot ^{-1} \frac{\sqrt{1-x^{2}}}{x}=\operatorname{cosec}^{-1} \frac{1}{x}=\sec ^{-1} \frac{1}{\sqrt{1-x^{2}}} \end{aligned} $

$ \begin{aligned} \cos ^{-1} \mathrm{x} & =\sin ^{-1} \sqrt{1-\mathrm{x}^{2}}=\tan ^{-1} \frac{\sqrt{1-\mathrm{x}^{2}}}{\mathrm{x}} \\ & =\cot ^{-1} \frac{\mathrm{x}}{\sqrt{1-\mathrm{x}^{2}}}=\operatorname{Cosec}^{-1} \frac{1}{\sqrt{1-\mathrm{x}^{2}}}=\sec ^{-1} \frac{1}{\mathrm{x}} \end{aligned} $

$ \begin{aligned} \tan ^{-1} \mathrm{x}= & \sin ^{-1} \frac{\mathrm{x}}{\sqrt{1+\mathrm{x}^{2}}}=\operatorname{Cos}^{-1} \frac{1}{\sqrt{1+\mathrm{x}^{2}}}=\cot ^{-1} \frac{1}{\mathrm{x}} \\ & \operatorname{cosec}^{-1} \frac{\sqrt{1+\mathrm{x}^{2}}}{\mathrm{x}}=\operatorname{Sec}^{-1} \sqrt{1+\mathrm{x}^{2}} \end{aligned} $
7. (i). $\sin ^{-1} x+\sin ^{-1} y=\left\{\begin{array}{l}\sin ^{-1}\left(x \sqrt{1-y^2}+y \sqrt{1-x^2}\right) \text { if }-1 \leq x, y \leq 1 &{\&} x^2+y^2 \leq 1 \\ \text { or if } x y<0 & {\&}x^2+y^2>1 \\ \pi-\sin ^{-1}\left(x \sqrt{1-y^2}+y \sqrt{1-x^2}\right) \text { if } 0<x, y \leq 1 & {\&}x^2+y^2>1 \\ -\pi-\sin ^{-1}\left(x \sqrt{1-y^2}+y \sqrt{1-x^2}\right) \text { if }-1 \leq x, y<0 & {\&}x^2+y^2>1\end{array}\right.$
(ii). $\sin ^{-1} x-\sin ^{-1} y=\left\{\begin{array}{l}\sin ^{-1}\left(x \sqrt{1-y^2}-y \sqrt{1-x^2}\right) \text { if }-1 \leq x, y \leq 1 & x^2+y^2 \leq 1 \\ \text { or if } x y>0 & x^2+y^2>1 \\ \pi-\sin ^{-1}\left(x \sqrt{1-y^2}-y \sqrt{1-x^2}\right) \text { if } 0<x \leq 1,-1<y \leq 0 & x^2+y^2>1 \\ -\pi-\sin ^{-1}\left(x \sqrt{1-y^2}-y \sqrt{1-x^2}\right) \text { if }-1 \leq x<0,0<y \leq 1 & x^2+y^2>1\end{array}\right.$
8. (i). $\cos ^{-1} \mathrm{x}+\cos ^{-1} \mathrm{y}=\left\{\begin{array}{l}\cos ^{-1}\left(\mathrm{xy}-\sqrt{1-\mathrm{x}^{2}} \sqrt{1-\mathrm{y}^{2}}\right) \text { if }-1 \leq \mathrm{x}, \mathrm{y} \leq 1 \& \mathrm{x}+\mathrm{y} \geq 0 \\ 2 \pi-\cos ^{-1}\left(\mathrm{xy}-\sqrt{1-\mathrm{x}^{2}} \sqrt{1-\mathrm{y}^{2}}\right) \text { if }-1 \leq \mathrm{x}, \mathrm{y} \leq 1 \& \mathrm{x}+\mathrm{y} \leq 0\end{array}\right.$
(ii). $\quad \cos ^{-1} x-\cos ^{-1} y=\left\{\begin{array}{l}\cos ^{-1}\left(x y+\sqrt{1-x^{2}} \sqrt{1-y^{2}}\right) \text { if }-1 \leq x, y \leq 1 \& x \leq y \\ -\cos ^{-1}\left(x y+\sqrt{1-x^{2}} \sqrt{1-y^{2}}\right) \text { if }-1 \leq y \leq 0,0<x \leq 1 \& x \geq y\end{array}\right.$
9. (i). $\tan ^{-1} x+\tan ^{-1} y=\left\{\begin{array}{l}\tan ^{-1}\left(\frac{x+y}{1-x y}\right) \text { if } x y<1 \\ \pi+\tan ^{-1}\left(\frac{x+y}{1-x y}\right) \text { if } x>0, y>0 x y>1 \\ -\pi+\tan ^{-1}\left(\frac{x+y}{1-x y}\right) \text { if } x<0, y<0 x y>1\end{array}\right.$
(ii). $\tan ^{-1} x-\tan ^{-1} y=\left\{\begin{array}{l}\tan ^{-1}\left(\frac{x-y}{1+x y}\right) \text { if } x y>-1 \\ \pi+\tan ^{-1}\left(\frac{x-y}{1+x y}\right) \text { if } x>0, y<0 \& x y<-1 \\ -\pi+\tan ^{-1}\left(\frac{x-y}{1+x y}\right), \text { if } x<0, y>0 \text { \& } x y<-1\end{array}\right.$
Remark : If $x _{1}, \quad x _{2}, \ldots \ldots \ldots . x _{n} \in R$, then $\tan ^{-1} x _{1}+\tan ^{-1} x _{2}+\ldots \ldots \ldots+\tan ^{-1} x _{n}$ $=\tan ^{-1}\left(\frac{\mathrm{s} _{1}-\mathrm{s} _{3}+\mathrm{s} _{5}-\mathrm{s} _{7} \ldots \ldots . .}{1-\mathrm{s} _{2}+\mathrm{s} _{4}-\mathrm{s} _{6}+\ldots \ldots .}\right)$
Where $\mathrm{s} _{\mathrm{k}}$ is the sum of the product of $\mathrm{x} _{1}, \mathrm{x} _{2}……….x_n$ taken $k$ at $a$ time.
ie. $\mathrm{s} _{1}=\mathrm{x} _{1}+\mathrm{x} _{2}+\ldots \ldots \ldots+\mathrm{x} _{\mathrm{n}}=\sum \mathrm{x} _{\mathrm{i}}$
$ \mathrm{s} _{2}=\quad \mathrm{x} _{1} \mathrm{x} _{2}+\mathrm{x} _{2} \mathrm{x} _{3}+\ldots \ldots .+\mathrm{x} _{\mathrm{n}-1}^{\mathrm{n}} \mathrm{x} _{\mathrm{n}}=\sum \mathrm{x} _{1} \mathrm{x} _{2} $
$\mathrm{s} _{3}=\quad \sum \mathrm{x} _{1} \mathrm{x} _{2} \mathrm{x} _{3}………$etc.
10. (i). $\quad 2 \sin ^{-1} x=\left\{\begin{array}{l}\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right) \text { if } \frac{-1}{\sqrt{2}} \leq x \leq \frac{1}{\sqrt{2}} \\ \pi-\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right), \text { if } \frac{1}{\sqrt{2}} \leq x \leq 1 \\ -\pi-\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right), \text { if }-1 \leq x \leq \frac{-1}{\sqrt{2}}\end{array}\right.$
(ii). $3 \sin ^{-1} x=\left\{\begin{array}{l}\sin ^{-1}\left(3 x-4 x^{3}\right), \text { if } \frac{-1}{2} \leq x \leq \frac{1}{2} \\ \pi-\sin ^{-1}\left(3 x-4 x^{3}\right), \text { if } \frac{1}{2}<x \leq 1 \\ -\pi-\sin ^{-1}\left(3 x-4 x^{3}\right), \text { if }-1 \leq x<\frac{-1}{2}\end{array}\right.$
11. (i). $2 \cos ^{-1} x=\left\{\begin{array}{l}\cos ^{-1}\left(2 x^{2}-1\right), \text { if } 0 \leq x \leq 1 \\ 2 \pi-\cos ^{-1}\left(2 x^{2}-1\right) \text { if }-1 \leq x \leq 0\end{array}\right.$
(ii). $\quad 3 \cos ^{-1} x=\left\{\begin{array}{l}\cos ^{-1}\left(4 x^{3}-3 x\right), \text { if } \frac{1}{2} \leq x \leq 1 \\ 2 \pi-\cos ^{-1}\left(4 x^{3}-3 x\right), \text { if } \frac{-1}{2} \leq x \leq \frac{1}{2} \\ 2 \pi+\cos ^{-1}\left(4 x^{3}-3 x\right), \text { if }-1 \leq x \leq \frac{-1}{2}\end{array}\right.$
12. (i). $2 \tan ^{-1} x=\left\{\begin{array}{l}\tan ^{-1}\left(\frac{2 x}{1-x^2}\right), \text { if }-1<x<1 \\ \pi+\tan ^{-1}\left(\frac{2 x}{1-x^2}\right), \text { if } x>1 \\ -\pi+\tan ^{-1}\left(\frac{2 x}{1-x^2}\right), \text { if } x<-1\end{array}\right.$
(ii). $3 \tan ^{-1} x=\left\{\begin{array}{l}\tan ^{-1}\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right), \text { if } \frac{-1}{\sqrt{3}}<x<\frac{1}{\sqrt{3}} \\ \pi+\tan ^{-1}\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right), \text { if } x>\frac{1}{\sqrt{3}} \\ -\pi+\tan ^{-1}\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right), \text { if } x<\frac{1}{\sqrt{3}}\end{array}\right.$
Note: If $|x| \leq 1$ then $2 \tan ^{-1} x=\sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right)=\cos ^{-1}\left(\frac{1-x^{2}}{1+x^{2}}\right)=\tan ^{-1}\left(\frac{2 x}{1-x^{2}}\right)$.
If $|x|>1$, change $x$ to $\frac{1}{x}$ in the above.
Note: In cases of identities in inverse trigonometric functions, principal values are to be taken. As such signs of $x, y$ etc., will determine the quadrant in which the angles will fall. In order to bring the angles of both sides in the same quadrant, adjustment by $\pi$ is to be made.
Examples
1. Evaluate $\tan ^{-1} \tan (-6)$
Show Answer
Solution:
We know that $\tan ^{-1}(\tan \theta)=\theta$ if $-\frac{\pi}{2}<\theta \frac{\pi}{2}$
$\therefore(2 \pi-6) \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$
$\tan (2 \pi-6)=-\tan 6=\tan (-6)$
Therefore $\tan ^{-1} \tan (-6)=\tan ^{-1} \tan (2 \pi-6)=2 \pi-6$
2. If $2 \tan ^{-1} x+\sin ^{-1} \frac{2 x}{1+x^{2}}$ is independent of $x$, then
(a). $\mathrm{x} \in[1, \infty)$
(b). $\mathrm{x} \in[-1,1]$
(c). $\mathrm{x} \in(-\infty,-1]$
(d). None of these
Show Answer
Solution:
$ \operatorname{\sin}^{-1} 2 x=\left\{\begin{array}{l} \pi-2 \tan ^{-1} x, x \geq 1 \\ -\left(\pi+2 \tan ^{-1} x\right) x \leq-1 \\ 2\tan ^{-1} x,|x|<1 \end{array}\right. $
$\therefore 2 \tan ^{-1} \mathrm{x}+\pi-2 \tan ^{-1} \mathrm{x}=\pi \quad$ when $\mathrm{x} \in[1, \infty)$
and $2 \tan ^{-1} \mathrm{x}-\pi-2 \tan ^{-1} \mathrm{x}=-\pi$ when $\mathrm{x} \in(-\infty,-1]$
Answer: a, c.
3. If $0<x<1$, then $\sqrt{1+x^{2}}\left[\left\{x \cos \left(\cot ^{-1} x\right)+\sin \left(\cot ^{-1} x\right)\right\}^{2}-1\right]^{1 / 2}=$
(a). $\frac{\mathrm{x}}{\sqrt{1+\mathrm{x}^{2}}}$
(b). $\mathrm{x}$
(c). $\mathrm{x} \sqrt{1+\mathrm{x}^{2}}$
(d). $\sqrt{1+\mathrm{x}^{2}}$
Show Answer
Solution:
$ \begin{aligned} & \sqrt{1+x^{2}}\left[\left\{x \cos ^{-1} \frac{x}{\sqrt{1+x^{2}}}+\sin \sin ^{-1} \frac{1}{\sqrt{1+x^{2}}}\right\}^{2}-1\right]^{1 / 2} \\ & \sqrt{1+x^{2}}\left[\left\{x \frac{x}{\sqrt{1+x^{2}}}+\frac{1}{\sqrt{1+x^{2}}}\right\}^{2}-1\right]^{1 / 2} \\ & \sqrt{1+x^{2}}\left[\left(\sqrt{1+x^{2}}\right)^{2}-1\right]^{1 / 2}=\sqrt{1+x^{2}} \cdot x \end{aligned} $
Answer: (c)
4. If $x \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$, then the value of $\tan ^{-1}\left(\frac{\tan x}{4}\right)+\tan ^{-1}\left(\frac{3 \sin 2 x}{5+3 \cos 2 x}\right)$ is
(a). $\frac{x}{2}$
(b). $2 \mathrm{x}$
(c). $3 \mathrm{x}$
(d). $x$
Show Answer
Solution:
$\tan ^{-1}\left(\frac{\tan x}{4}\right)+\tan ^{-1}\left(\frac{\frac{6 \tan x}{1+\tan ^{2} x}}{5+\frac{3\left(1-\tan ^{2} x\right)}{1+\tan ^{2} x}}\right)$
$\tan ^{-1}\left(\frac{\tan x}{4}\right)+\tan ^{-1}\left(\frac{6 \tan x}{8+2 \tan ^{2} x}\right)$
$\tan ^{-1}\left(\frac{\frac{\tan x}{4}+\frac{3 \tan x}{4+\tan ^{2} x}}{1-\frac{3 \tan ^{2} x}{4\left(4+\tan ^{2} x\right)}}\right)$ as $\left|\frac{\tan x}{4} \cdot \frac{3 \tan x}{4+\tan ^{2} x}\right|<1$
$\tan ^{-1}\left(\frac{16 \tan x+\tan ^{3} x}{16+\tan ^{2} x}\right)$
$\tan ^{-1}(\tan x)$
Answer: d.
5. An integral solution of the equation
$\tan ^{-1} x+\tan ^{-1} \frac{1}{y}=\tan ^{-1} 3$ is
(a). $(2,7)$
(b). $(4,-13)$
(c). $(5,-8)$
(d). $(1,2)$
Show Answer
Solution:
$ \begin{aligned} & \tan ^{-1} x+\tan ^{-1} \frac{1}{y}=\tan ^{-1} 3 \\ & \tan ^{-1}\left(\frac{x+\frac{1}{y}}{1-\frac{x}{y}}\right)=\tan ^{-1} 3 \text { if } \frac{x}{y}<1 \\ & \frac{x+\frac{1}{y}}{1-\frac{x}{y}}=3 \\ & x+\frac{1}{y}=3-\frac{3 x}{y} \\ & y=\frac{3 x+1}{3-x} \end{aligned} $
which satisfied by options a, b, c and d
Answer: a, b, c, d
6. Sum to the $\mathrm{n}$ terms of the series
$\operatorname{cosec}^{-1} \sqrt{10}+\operatorname{cosec}^{-1} \sqrt{50}+\operatorname{cosec}^{-1} \sqrt{170}+$. $+\operatorname{cosec}^{-1} \sqrt{\left(n^{2}+1\right)\left(n^{2}+2 n+2\right)}$ is
(a). $0$
(b). $\infty$
(c). $\tan ^{-1}(\mathrm{n}+1)-\frac{\pi}{4}$
(d). $\cot ^{-1}(n+1)-\frac{\pi}{4}$
Show Answer
Solution:
$ \begin{aligned} & \text { Let } \theta=\operatorname{cosec}^{-1} \sqrt{\left(\mathrm{n}^{2}+1\right)\left(\mathrm{n}^{2}+2 \mathrm{n}+2\right)} \\ & \operatorname{cosec}^{2} \theta=\left(\mathrm{n}^{2}+1\right)\left(\mathrm{n}^{2}+2 \mathrm{n}+2\right) \\ &=\left(\mathrm{n}^{2}+1\right)^{2}+2 \mathrm{n}\left(\mathrm{n}^{2}+1\right)+\mathrm{n}^{2}+1 \\ & 1+\cot ^{2} \theta=\left(\mathrm{n}^{2}+\mathrm{n}+1\right)^{2}+1 \\ & \cot \theta \quad=\mathrm{n}^{2}+\mathrm{n}+1 \\ & \tan \theta \quad=\frac{1}{\mathrm{n}^{2}+\mathrm{n}+1}=\frac{(\mathrm{n}+1)-\mathrm{n}}{1+(\mathrm{n}+1) \mathrm{n}} \\ & \theta \quad=\tan ^{-1}(\mathrm{n}+1)-\tan ^{-1} \mathrm{n} \\ & \text { Thus, sum to n terms of the series } \\ &=\left(\tan ^{-1} 2-\tan ^{-1} 1\right)+\left(\tan ^{-1} 3-\tan ^{-1} 2\right)+\ldots \ldots \ldots . .+\left(\tan ^{-1}(\mathrm{n}+1)-\tan ^{-1} \mathrm{n}\right) \\ &=\tan ^{-1}(\mathrm{n}+1)-\tan ^{-1} 1 \\ &=\tan ^{-1}(\mathrm{n}+1)-\frac{\pi}{4} \end{aligned} $
Answer: c
7. In a $\triangle \mathrm{ABC}$, if $\mathrm{A}=\tan ^{-1} 2, \mathrm{~B}=\tan ^{-1} 3$ then $\mathrm{C}$ is equal to
(a). $\frac{\pi}{3}$
(b). $\frac{\pi}{4}$
(c). $\frac{\pi}{6}$
(d). None of these
Show Answer
Solution:
$ \begin{aligned} & \mathrm{A}+\mathrm{B}+\mathrm{C}=\pi \\ & \mathrm{C}=\pi _{-}(\mathrm{A}+\mathrm{B}) \\ & =\pi _{-}\left(\tan ^{-1} 2+\tan ^{-1} 3\right) \\ & =\pi _{-}\left\{\pi+\tan ^{-1} \frac{5}{1-6}\right\}\quad \because x y>1 \\ & =\pi _{-} \pi _{+\tan ^{-1} 1} \\ & =\frac{\pi}{4} \end{aligned} $
Answer: b
Practice questions
1. If $x$ satisfies the inequation $x^{2}-x-2>0$, then a value exits for
(a). $\sin ^{-1} x$
(b). $\sec ^{-1} \mathrm{x}$
(c). $\cos ^{-1} \mathrm{x}$
(d). None of these
Show Answer
Answer: (b)2. If $\left[\sin ^{-1} x\right]+\left[\cos ^{-1} x\right]=0$, where $x$ is a non negative real number and [.] denotes the greatest integer function, then complete set of values of $x$ is
(a). $(\cos 1,1)$
(b). $(-1, \cos 1)$
(c). $(\sin 1,1)$
(d). $(\cos 1, \sin 1)$
Show Answer
Answer: (d)3. If $\cos ^{-1} x+\cos ^{-1} y+\cos ^{-1} z=3 \pi$, then $x y+y z+z x$ is
(a). $-3$
(b). $0$
(c). $3$
(d). $\pi$
Show Answer
Answer: (c)4. If $\sin ^{-1} x+\sin ^{-1} y=\frac{2 \pi}{3}$ then $\cos ^{-1} x+\cos ^{-1} y=$
(a). $\frac{2 \pi}{3}$
(b). $\frac{\pi}{3}$
(c). $\frac{\pi}{6}$
(d). $\pi$
Show Answer
Answer: (b)5. The greatest of $\tan 1, \tan ^{-1} 1, \sin ^{-1} 1, \sin 1, \cos 1$ is
(a). $\sin 1$
(b). $\tan 1$
(c). $\tan ^{-1} 1$
(d). None of these
Show Answer
Answer: (b)6. The value of $\cos ^{-1}(\cos 12)-\sin ^{-1}(\sin 12)$ is
(a). $0$
(b). $\pi$
(c). $8 \pi-24$
(d). None of these
Show Answer
Answer: (c)7. $\cot ^{-1}(\sqrt{\cos \alpha})-\tan ^{-1}(\sqrt{\cos \alpha})=x$, then $\sin x=$
(a). $\tan ^{2} \frac{\alpha}{2}$
(b). $\cot ^{2} \frac{\alpha}{2}$
(c). $\tan \alpha$
(d). $\cot \frac{\alpha}{2}$
Show Answer
Answer: (a)8. If $\sin ^{-1} x=2 \sin ^{-1}$ a has a solution for
(a). $|\mathrm{a}| \geq \frac{1}{\sqrt{2}}$
(b). $|\mathrm{a}| \leq \frac{1}{\sqrt{2}}$
(c). all real values of a
(d). $|\mathrm{a}|<\frac{1}{2}$
Show Answer
Answer: (b)9. If $\cos ^{-1} x-\cos ^{-1} \frac{y}{2}=\alpha$, then $4 x^{2}-4 x y \cos \alpha+y^{2}$ is equal to
(a). $2 \sin 2 \alpha$
(b). $4$
(c). $4 \sin ^{2} \alpha$
(d). $-4 \sin ^{2} \alpha$
Show Answer
Answer: (c)10. If $\sin ^{-1}\left(\frac{x}{5}\right)+\operatorname{cosec}^{-1}\left(\frac{5}{4}\right)=\left(\frac{\pi}{2}\right)$, then the value of $x$ is
(a). 4
(b). 5
(c). 1
(d). 3
Show Answer
Answer: (d)11. The value of $\cot \left(\operatorname{cosec}^{-1} \frac{5}{3}+\tan ^{-1} \frac{2}{3}\right)$ is
(a). $\frac{6}{17}$
(b). $\frac{3}{17}$
(c). $\frac{4}{17}$
(d). $\frac{5}{17}$
Show Answer
Answer: (a)Assertion and Reasoning
12. $\operatorname{Let} f(x)=\sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right)$
Statement-1 : $ \mathrm{f}^{\prime}(2)=-\frac{2}{5}$ and
Statement-2:$\sin ^{-1}\left(\frac{2 \mathrm{x}}{1+\mathrm{x}^{2}}\right)=\pi-2 \tan ^{-1} \mathrm{x}, \forall \mathrm{x}>1$.
(a). Statement-1 is True, statement-2 is True ;statement-2 is a correct explanation for statement-1
(b). Statement-1 is True, statement - 2 is True ; statement - 2 is NOT a correct explanation for statement - 1
(c). Statement - 1 is True, statement - 2 is False
(d). Statement - 1 is False, statement - 2 is True.
Show Answer
Answer: (a)Comprehension (Que. no. 13 to 15)
$ \begin{aligned} \text { Given that } \tan ^{-1}\left(\frac{2 x}{1-x^{2}}\right) & = \begin{cases}2 \tan ^{-1} x, & |x| \leq 1 \\ -\pi+2 \tan ^{-1} x, & x>1 \\ \pi+2 \tan ^{-1} x, & x<-1\end{cases} \\ \sin ^{-1}\left(\frac{2 x}{1-x^{2}}\right) & = \begin{cases}2 \tan ^{-1} x, & x \mid \leq 1 \\ \pi-2 \tan ^{-1} x, & x>1 \\ -\left(\pi+2 \tan ^{-1} x\right), & x<-1\end{cases} \end{aligned} $
and $\sin ^{-1} \mathrm{x}+\cos ^{-1} \mathrm{x}=\frac{\pi}{2}$ for $-1 \leq \mathrm{x} \leq 1$.
13. $\sin ^{-1}\left(\frac{4 x}{x^{2}+4}\right)+2 \tan ^{-1}\left(-\frac{x}{2}\right)$ is independent at $x$ then :
(a). $\mathrm{x} \in[1, \infty)$
(b). $x \in[1,1]$
(c). $[-2,2]$
(d). $\mathrm{x} \in[-3,4]$
Show Answer
Answer: (c)14. If $(x-1)\left(x^{2}+1\right)>0$, then $\sin \left(\frac{1}{2} \tan ^{-1} \frac{2 x}{1-x^{2}}-\tan ^{-1} x\right)=$
(a). $-1$
(b). $1$
(c). $\frac{1}{\sqrt{2}}$
(d). None of these
Show Answer
Answer: (a)15. If $\cos ^{-1}\left(\frac{6 \mathrm{x}}{1+9 \mathrm{x}^{2}}\right)=-\frac{\pi}{2}+2 \tan ^{-1} 3 \mathrm{x}$ then $\mathrm{x} \in$
(a). $(-\infty,-1)$
(b). $\left(-\frac{1}{3}, \frac{1}{3}\right)$
(c). $\left(\frac{1}{3}, \infty\right)$
(d). None of these
Show Answer
Answer: (c)16. Match the following
| Column I | Column II |
|---|---|
| (a). If $\cos ^{-1} a+\cos ^{-1} b+\cos ^{-1} c=3 \pi$ then $a b+b c+c a$ is | (p). $2n$ |
| (b). $\sum _{\mathrm{i}=1}^{10} \cos ^{-1} \mathrm{x} _{\mathrm{i}}=0$, then $\sum _{\mathrm{i}=1}^{10} \mathrm{x} _{\mathrm{i}}$ | (q). $\sin^{-1}x-\frac{\pi}{6}$ |
| (c). $\sum _{\mathrm{i}=1}^{2 \mathrm{n}} \sin ^{-1} \mathrm{x} _{\mathrm{i}}=\mathrm{n} \pi$, then $\sum _{\mathrm{i}=1}^{2 \mathrm{n}} \mathrm{x} _{\mathrm{i}}$ is | (r). $3$ |
| (d). $f(x)=\sin ^{-1}\left\{\frac{\sqrt{3}}{2} x-\frac{1}{2} \sqrt{1-x^{2}}\right\},-\frac{1}{2} \leq x \leq 1$ is | (s). $10$ |





