TRIGONOMETRY TRIANGLES - 1 (Properties of Triangles)
Sine rule
1. $\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}=k$
or $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=\lambda$
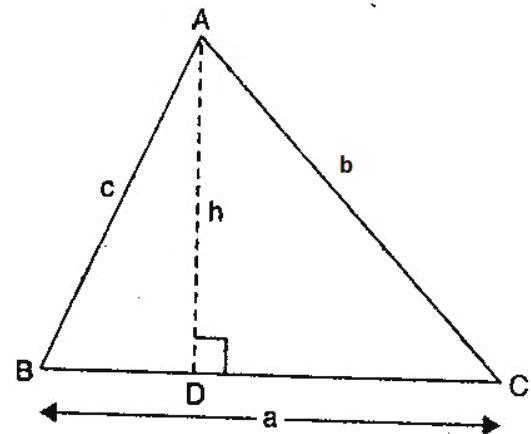
Cosine rule
2. (i). $\quad \cos \mathrm{A}=\frac{\mathrm{b}^{2}+\mathrm{c}^{2}-\mathrm{a}^{2}}{2 \mathrm{bc}}$
(ii). $\quad \cos \mathrm{B}=\frac{\mathrm{c}^{2}+\mathrm{a}^{2}-\mathrm{b}^{2}}{2 \mathrm{ca}}$
(iii). $\quad \cos \mathrm{C}=\frac{\mathrm{a}^{2}+\mathrm{b}^{2}-\mathrm{c}^{2}}{2 \mathrm{ab}}$
Projection formulae
3. (i). $\quad b \cos \mathrm{C}+\mathrm{c} \cos \mathrm{B}=\mathrm{a}$
(ii). $\quad \mathrm{c} \cos \mathrm{A}+\mathrm{a} \cos \mathrm{C}=\mathrm{b}$
(iii). $\quad a \cos \mathrm{B}+\mathrm{b} \cos \mathrm{A}=\mathrm{c}$
Napier’s analogy
4. (i). $\quad \tan \left(\frac{\mathrm{B}-\mathrm{C}}{2}\right)=\frac{\mathrm{b}-\mathrm{c}}{\mathrm{b}+\mathrm{c}} \cot \frac{\mathrm{A}}{2}$
(ii). $\quad \tan \left(\frac{\mathrm{C}-\mathrm{A}}{2}\right)=\frac{\mathrm{c}-\mathrm{a}}{\mathrm{c}+\mathrm{a}} \cot \frac{\mathrm{B}}{2}$
(iii). $\quad \tan \left(\frac{\mathrm{A}-\mathrm{B}}{2}\right)=\frac{\mathrm{a}-\mathrm{b}}{\mathrm{a}+\mathrm{b}} \cot \frac{\mathrm{C}}{2}$
5. (a). (i). $\sin \frac{\mathrm{A}}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})}{\mathrm{bc}}}$
(ii). $\quad \sin \frac{\mathrm{B}}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{c})(\mathrm{s}-\mathrm{a})}{\mathrm{ca}}}$
(iii). $\quad \sin \frac{\mathrm{C}}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{a})(\mathrm{s}-\mathrm{b})}{\mathrm{ab}}}$
(b). (i). $\quad \cos \frac{\mathrm{A}}{2}=\sqrt{\frac{\mathrm{s}(\mathrm{s}-\mathrm{a})}{\mathrm{bc}}}$
(ii). $\quad \cos \frac{\mathrm{B}}{2}=\sqrt{\frac{\mathrm{s}(\mathrm{s}-\mathrm{b})}{\mathrm{ca}}}$
(iii). $\quad \cos \frac{\mathrm{C}}{2}=\sqrt{\frac{\mathrm{s}(\mathrm{s}-\mathrm{c})}{\mathrm{ab}}}$
(c). (i). $\quad \tan \frac{\mathrm{A}}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})}{\mathrm{s}(\mathrm{s}-\mathrm{a})}}$
(ii). $\quad \tan \frac{\mathrm{B}}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{c})(\mathrm{s}-\mathrm{a})}{\mathrm{s}(\mathrm{s}-\mathrm{b})}}$
(iii). $\quad \tan \frac{\mathrm{C}}{2}=\sqrt{\frac{(\mathrm{s}-\mathrm{a})(\mathrm{s}-\mathrm{b})}{\mathrm{s}(\mathrm{s}-\mathrm{c})}}$
(d). (i). $\quad \cot \frac{\mathrm{A}}{2}=\sqrt{\frac{\mathrm{s}(\mathrm{s}-\mathrm{a})}{(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})}}$
(ii). $\quad \cot \frac{\mathrm{B}}{2}=\sqrt{\frac{\mathrm{s}(\mathrm{s}-\mathrm{b})}{(\mathrm{s}-\mathrm{c})(\mathrm{s}-\mathrm{a})}}$
(iii). $\quad \cot \frac{\mathrm{C}}{2}=\sqrt{\frac{\mathrm{s}(\mathrm{s}-\mathrm{c})}{(\mathrm{s}-\mathrm{a})(\mathrm{s}-\mathrm{b})}}$
(e). (i). $\quad \sin \mathrm{A}=\frac{2 \Delta}{\mathrm{bc}}=\frac{2}{\mathrm{bc}} \sqrt{\mathrm{s}(\mathrm{s}-\mathrm{a})(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})}$
(ii). $\quad \sin \mathrm{B}=\frac{2 \Delta}{\mathrm{ca}}=\frac{2}{\mathrm{ca}} \sqrt{\mathrm{s}(\mathrm{s}-\mathrm{a})(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})}$
(i). $\quad \sin \mathrm{C}=\frac{2 \Delta}{\mathrm{ab}}=\frac{2}{\mathrm{ab}} \sqrt{\mathrm{s}(\mathrm{s}-\mathrm{a})(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})}$
Radius of the circumcircle ‘R’
6. $\mathrm{R}=\frac{\mathrm{a}}{2 \sin \mathrm{A}}=\frac{\mathrm{b}}{2 \sin \mathrm{B}}=\frac{\mathrm{c}}{2 \sin \mathrm{C}}=\frac{\mathrm{abc}}{4 \Delta}$
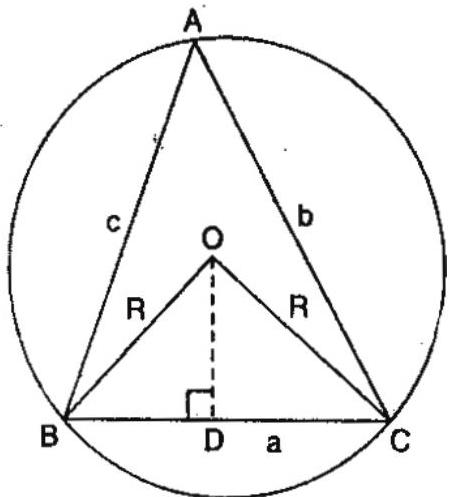
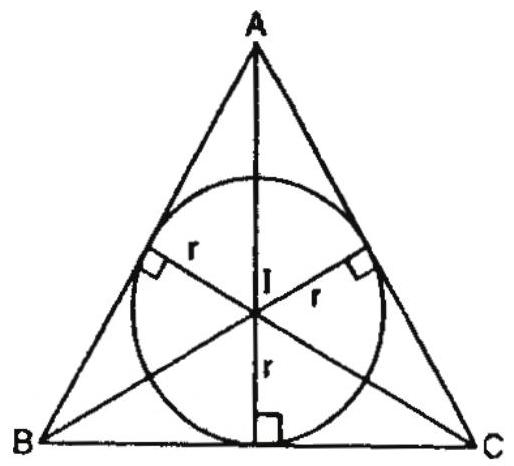
Radius of the incircle ‘$r$’
7. $\mathrm{r}=\frac{\Delta}{\mathrm{s}}=(\mathrm{s}-\mathrm{a}) \tan \frac{\mathrm{A}}{2}=(\mathrm{s}-\mathrm{b}) \tan \frac{\mathrm{B}}{2}=(\mathrm{s}-\mathrm{c}) \tan \frac{\mathrm{C}}{2}=4 \mathrm{R} \sin \frac{\mathrm{A}}{2} \sin \frac{\mathrm{B}}{2} \sin \frac{\mathrm{C}}{2}$
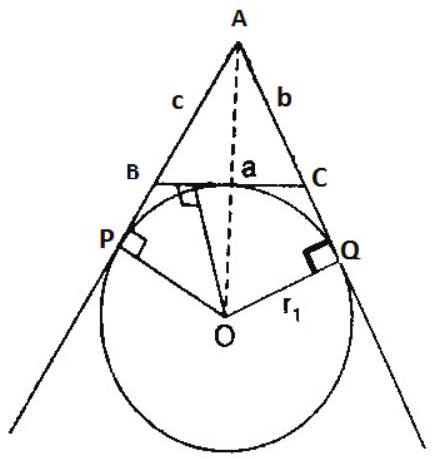
Radii of the excircles $r _{1}, r _{2}$ and $r _{3}$
8. (i). $\quad \mathrm{r} _{1}=\frac{\Delta}{\mathrm{s}-\mathrm{a}}=\mathrm{stan} \frac{\mathrm{A}}{2}=4 \mathrm{R} \sin \frac{\mathrm{A}}{2} \cos \frac{\mathrm{B}}{2} \cos \frac{\mathrm{C}}{2}$
(ii). $\quad \mathrm{r} _{2}=\frac{\Delta}{\mathrm{s}-\mathrm{b}}=\mathrm{s} \tan \frac{\mathrm{B}}{2}=4 \mathrm{R} \cos \frac{\mathrm{A}}{2} \sin \frac{\mathrm{B}}{2} \cos \frac{\mathrm{C}}{2}$
(iii). $\quad r _{3}=\frac{\Delta}{s-c}=s \tan \frac{C}{2}=4 R \cos \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}$
(iv). $\quad r _{1}=\frac{a \cos \frac{B}{2} \cos \frac{C}{2}}{\cos \frac{A}{2}}$ etc
(v). $\quad \mathrm{r} _{1}+\mathrm{r} _{2}+\mathrm{r} _{3}=\mathrm{r}+4 \mathrm{r}$
(vi). $\quad \frac{1}{\mathrm{r} _{1}}+\frac{1}{\mathrm{r} _{2}}+\frac{1}{\mathrm{r} _{3}}=\frac{1}{\mathrm{r}}$
(vii). $\quad \mathrm{r} _{1} \mathrm{r} _{2}+\mathrm{r} _{2} \mathrm{r} _{3}+\mathrm{r} _{3} \mathrm{r} _{1}=\mathrm{s}^{2}$
(viii). $\quad a \cos A+b \cos B+c \cos C=4 R \sin A \sin B \sin C$
(ix). $\quad a \cot \mathrm{A}+\mathrm{b} \cot \mathrm{B}+\mathrm{c} \cot \mathrm{C}=2(\mathrm{R}+\mathrm{r})$
Also, $r=\frac{a \sin \frac{B}{2} \sin \frac{C}{2}}{\cos \frac{A}{2}}=\frac{b \sin \frac{C}{2} \sin \frac{A}{2}}{\cos \frac{B}{2}}=\frac{c \sin \frac{A}{2} \sin \frac{B}{2}}{\cos \frac{C}{2}}$
9. If length of the median $\mathrm{AD}, \mathrm{BE}$ and $\mathrm{CF}$ are given, then sides can be determined by using the formula
$ \mathrm{a}^{2}=\frac{4}{3}\left(2 \mathrm{BE}^{2}+2 \mathrm{CF}^{2}-\mathrm{AD}^{2}\right) $
Similarly $\quad b^{2}=\frac{4}{3}\left(2 \mathrm{CF}^{2}+2 \mathrm{AD}^{2}-\mathrm{BE}^{2}\right)$
and $\mathrm{c}^{2}=\frac{4}{3}\left(2 \mathrm{AD}^{2}+2 \mathrm{BE}^{2}-\mathrm{CF}^{2}\right)$
10. Distance of the orthocentre from the vertex $A$ is $2 R \cos A$.
Pedal triangle
11. Triangle formed by joining the foot of perpendiculars drawn from vertices to opposite sides of a given tri-angle is called pedal triangle.
Length of the sides of pedal triangle of given $\triangle \mathrm{ABC}$ are $\mathrm{a} \cos \mathrm{A}, \mathrm{b} \cos \mathrm{B}$ and $\mathrm{c} \cos \mathrm{C}$ respectively. Angles of the pedal triangle are $180^{\circ}-2 \mathrm{~A}, 180^{\circ}-2 \mathrm{~B}$ and $180^{\circ}-2 \mathrm{C}$ respectively.
Excentric triangle
12. If $\mathrm{I} _{1}, \mathrm{I} _{2}$, and $\mathrm{I} _{3}$ are the centres of excircles, then $\Delta \mathrm{I} _{1} \mathrm{I} _{2} \mathrm{I} _{3}$ is called excentric triangle. $\mathrm{I} _{2}, \mathrm{~A}, \mathrm{I} _{3}$;
$\mathrm{I} _{3}, \mathrm{~B}, \mathrm{I} _{1}$ and $\mathrm{I} _{2}, \mathrm{C}, 1 _{2}$ are collinear. $\triangle \mathrm{ABC}$ is the pedal $\Delta$ of $\Delta \mathrm{I} _{1} \mathrm{I} _{2} \mathrm{I} _{3}$. Incentre ’ $\mathrm{I}$ ’ of the $\triangle \mathrm{ABC}$ will be orthocentre of $\Delta \mathrm{I} _{1} \mathrm{I} _{2} \mathrm{I} _{3}$.
13. If median $\mathrm{AD}$ inclined at angles $\alpha, \beta, \gamma$ with $\mathrm{BC}, \mathrm{CA}$ and $\mathrm{AB}$ respectively then
$\sin \alpha=\frac{b \sin C}{\sqrt{2 b^{2}+2 c^{2}-a^{2}}}$
$\sin \beta=\frac{\mathrm{a} \sin \mathrm{C}}{\sqrt{2 \mathrm{~b}^{2}+2 \mathrm{c}^{2}-\mathrm{a}^{2}}}$ and $\sin \gamma=\frac{\mathrm{a} \sin \mathrm{B}}{\sqrt{2 \mathrm{~b}^{2}+2 \mathrm{c}^{2}-\mathrm{a}^{2}}}$
14. Distance between orthocentre and circumcentre
$=R \sqrt{1-8 \cos A \cos B \cos C}$
15. Distance between circumcentre and incentre is
$R \sqrt{1-8 \sin \frac{\mathrm{A}}{2} \sin \frac{\mathrm{B}}{2} \sin \frac{\mathrm{C}}{2}}=\sqrt{\mathrm{R}(\mathrm{R}-2 \mathrm{r})}$
16. Distance between circumcentre and centre of excircles are
$\mathrm{OI} _{1} \mathrm{R} \sqrt{1+8 \sin \frac{\mathrm{A}}{2} \cos \frac{\mathrm{B}}{2} \cos \frac{\mathrm{C}}{2}}=\sqrt{\mathrm{R}\left(\mathrm{R}+2 \mathrm{r} _{1}\right)}$
$\mathrm{OI} _{2} \mathrm{R} \sqrt{1+8 \cos \frac{\mathrm{A}}{2} \sin \frac{\mathrm{B}}{2} \cos \frac{\mathrm{C}}{2}}=\sqrt{\mathrm{R}\left(\mathrm{R}+2 \mathrm{r} _{2}\right)}$
$\mathrm{OI} _{3} \mathrm{R} \sqrt{1+8 \cos \frac{\mathrm{A}}{2} \cos \frac{\mathrm{B}}{2} \sin \frac{\mathrm{C}}{2}}=\sqrt{\mathrm{R}\left(\mathrm{R}+2 \mathrm{r} _{3}\right)}$
17. Length of the angle bisectors
$A D=\frac{2 b c}{b+c} \cos \frac{A}{2}=\frac{b c \sin A}{b+c \sin \frac{A}{2}}$
$\mathrm{BE}=\frac{2 \mathrm{ca}}{\mathrm{c}+\mathrm{a}} \cos \frac{\mathrm{B}}{2}$ and $\mathrm{CF}=\frac{2 \mathrm{ab}}{\mathrm{a}+\mathrm{b}} \cos \frac{\mathrm{C}}{2}$
18. Area of quadrilateral $\mathrm{ABCD}$, if sum of a pair opposite angle is $2 \alpha$ is
$\sqrt{(s-a)(s-b)(s-c)(s-d)-a b c d \cos ^{2} \alpha}$
where $2 \mathrm{~s}=\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}$
19. $\mathrm{m}-\mathrm{n}$ theorem
$(\mathrm{m}+\mathrm{n}) \cot \theta=\mathrm{m} \cot \alpha-\mathrm{n} \cot \beta$
$(\mathrm{m}+\mathrm{n}) \cot \theta=\mathrm{n} \cot \mathrm{B}-\mathrm{m} \cot \mathrm{C}$

Some extra tips
1. $\quad$i. $\quad \sum \mathrm{a}^{3} \sin (\mathrm{B}-\mathrm{C})=0$
$\quad$ $\quad$ii. $\quad \sum \mathrm{a}^{3} \cos (\mathrm{B}-\mathrm{C})=3 \mathrm{abc}$
2. $\quad$(i). If $a \cos B=b \cos A$, then the triangle is isosceles
$\quad$ (ii). $\quad$If $a \cos \mathrm{A}=\mathrm{b} \cos \mathrm{B}$, then the triangle is isosceles or right angled
$\quad$ (iii). $\quad$If $\mathrm{a}^{2}+\mathrm{b}^{2}+\mathrm{c}^{2}=8 \mathrm{R}^{2}$, then the triangle is right angled
$\quad$ (iv). $\quad$If $\cos ^{2} \mathrm{~A}+\cos ^{2} \mathrm{~B}+\cos ^{2} \mathrm{C}=1$, then the triangle is right angled
$\quad$ (v). $\quad$If $\cos A=\frac{\sin B}{2 \sin C}$, then the triangle is isosceles
$\quad$ (vi). $\quad$If $\frac{\mathrm{a}}{\cos \mathrm{A}}=\frac{\mathrm{b}}{\cos \mathrm{B}}=\frac{\mathrm{c}}{\cos \mathrm{C}}$, then the triangle is equilateral
$\quad$ (vii). $\quad$If $\cos \mathrm{A}+\cos \mathrm{B}+\cos \mathrm{C}=\frac{3}{2}$, then the triangle is equilateral
$\quad$ (viii). $\quad$If $\sin \mathrm{A}+\sin \mathrm{B}+\sin \mathrm{C}=\frac{3 \sqrt{3}}{2}$, then the triangle is equilateral
$\quad$ (ix). $\quad$If $\tan A+\tan B+\tan C=3 \sqrt{3}$, then the triangle is equilateral
$\quad$ (x). $\quad$If $\cot A+\cot B+\cot C=\sqrt{3}$, then the triangle is equilateral
3. (a). The circumcentre lies (i) inside an acute angled triangle (ii) outside an obtuse angled triangle.
$\quad$ (b). The circumcircle of a right angled triangle is the mid point of the hypotenuse.
$\quad$ (c). The orthocentre of a right angled triangle is the vertex at the right angle.
4. Triangle is equilateral if any one of the following holds:
$\quad$ (a). $\mathrm{R}=2 \mathrm{r}$
$\quad$ (b). $r _{1}=r _{2}=r _{3}$
$\quad$ (c). $r: R: r _{1}=1: 2: 3$
5. Triangle is right angled if $r: R: r _{1}=2: 5: 12$
6. If $\mathrm{r} _{1}, \mathrm{r} _{2}, \mathrm{r} _{3}$ are in H.P. iff $\mathrm{a}, \mathrm{b}, \mathrm{c}$ are in A.P.
7. In an equilateral triangle:
$\quad$ (a). area $=\frac{\sqrt{3} \mathrm{a}^{2}}{4}$
$\quad$ (b). $ \mathrm{R}=\frac{\mathrm{a}}{\sqrt{3}}$
$\quad$ (c). $ r=\frac{R}{2}$
$\quad$ (d). $r _{1}=r _{2}=r _{3}=\frac{3 R}{2}$
$\quad$ e. $\mathrm{r}=\mathrm{R}=\mathrm{r} _{1}=1: 2: 3$
Examples
1. In triangle $\mathrm{ABC}, 2 \mathrm{ac} \sin \left(\frac{1}{2}(\mathrm{~A}-\mathrm{B}+\mathrm{C})\right.$ is equal to
(a). $\mathrm{a}^{2}+\mathrm{b}^{2}-\mathrm{c}^{2}$
(b). $\mathrm{c}^{2}+\mathrm{a}^{2}-\mathrm{b}^{2}$
(c). $\mathrm{b}^{2}-\mathrm{c}^{2}-\mathrm{a}^{2}$
(d). $\mathrm{c}^{2}-\mathrm{a}^{2}-\mathrm{b}^{2}$
Show Answer
Solution:
Given that $2 \mathrm{ac} \sin \left(\frac{1}{2}(\mathrm{~A}-\mathrm{B}+\mathrm{C})\right.$
$ \begin{aligned} & =2 \mathrm{ac} \sin \left(\frac{1}{2}(\pi-2 \mathrm{~B})\right) \\ & =2 \mathrm{ac} \sin \left(\left(\frac{\pi}{2}-\mathrm{B}\right)\right) \\ & =2 \mathrm{ac} \cos \mathrm{B} \\ & =2 \mathrm{ac}\left(\frac{\mathrm{a}^{2}+\mathrm{c}^{2}-\mathrm{b}^{2}}{2 \mathrm{ac}}\right) \\ & =\mathrm{a}^{2}+\mathrm{c}^{2}-\mathrm{b}^{2} \end{aligned} $
Correct option is ‘b’
2. Let $\mathrm{ABC}$ be a triangle such that $\angle \mathrm{ACB}=\frac{\pi}{6}$ and let $\mathrm{a}, \mathrm{b}$ and $\mathrm{c}$ denote the lengths of the side opposite to $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$, respectively. The values of $\mathrm{x}$ for which $\mathrm{a}=\mathrm{x}^{2}+\mathrm{x}+1, \mathrm{~b}=\mathrm{x}^{2}-1$ and $\mathrm{c}=2 \mathrm{x}+1$ is (are)
(a). $-(2+\sqrt{3})$
(b). $1+\sqrt{3}$
(c). $2+\sqrt{3}$
(d). $4 \sqrt{3}$
Show Answer
Solution:
Given that $\angle \mathrm{ACB}=\frac{\pi}{6}$
$\cos (\angle \mathrm{ACB})=\cos \mathrm{C}=\frac{\mathrm{a}^{2}+\mathrm{b}^{2}-\mathrm{c}^{2}}{2 \mathrm{ab}}$
$\cos \frac{\pi}{6}=\frac{\left(\mathrm{x}^{2}+\mathrm{x}+1\right)^{2}+\left(\mathrm{x}^{2}-1\right)^{2}-(2 \mathrm{x}+1)^{2}}{2\left(\mathrm{x}^{2}+\mathrm{x}+1\right)\left(\mathrm{x}^{2}-1\right)}$
$\frac{\sqrt{3}}{2}=\frac{\left.\left(x^{2}+3 x+2\right)\left(x^{2}-x\right)+x^{2}-1\right)^{2}}{2\left(x^{2}+x+1\right)\left(x^{2}-1\right)} \Rightarrow \frac{\sqrt{3}}{2}=\frac{2 x^{4}+2 x^{3}-3 x^{2}-2 x+1}{2\left(x^{2}+x+1\right)\left(x^{2}-1\right)}$
$\sqrt{3}=\frac{x\left(x^{2}+3 x+2\right)+x^{2}-1}{x^{2}+x+1} \quad=\frac{\sqrt{3}}{2}=\frac{\left(2 x^{2}-2 x-1\right)\left(x^{2}-1\right)}{2\left(x^{2}+x+1\right)\left(x^{2}-1\right)}$
$\sqrt{3}=\frac{2 x^{2}+2 x-1}{x^{2}+x+1}$
$ \begin{aligned} & (\sqrt{3}-2) x^{2}+(\sqrt{3}-2) x+(\sqrt{3}+1)=0 \\ & x=\frac{(2-\sqrt{3}) \pm \sqrt{3}}{2(\sqrt{3}-2)} \\ & x=-(2+\sqrt{3}), 1+\sqrt{3} \\ & \text { as } x>0 \therefore x=1+\sqrt{3} \end{aligned} $
Correct option is ‘b’
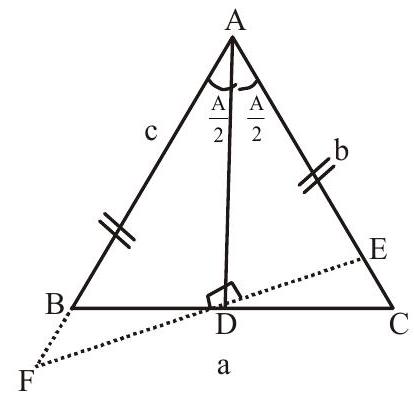
3. In $\triangle \mathrm{ABC}$, interval angle bisector of $\angle \mathrm{A}$ meets side $\mathrm{BC}$ in $\mathrm{D}$. $\mathrm{DE} \perp \mathrm{AD}$ meets $\mathrm{AC}$ in $\mathrm{E}$ and $\mathrm{AB}$ in F. Then
(a). $\mathrm{AE}$ is $\mathrm{HM}$ of $\mathrm{b}$ and $\mathrm{c}$
(b). $\mathrm{AD}=\frac{2 \mathrm{bc}}{\mathrm{b}+\mathrm{c}} \cos \frac{\mathrm{A}}{2}$
(c). $\mathrm{EF}=\frac{4 \mathrm{bc}}{\mathrm{b}+\mathrm{c}} \sin \frac{\mathrm{A}}{2}$
(d). $\triangle \mathrm{AEF}$ is isosceles
Show Answer
Solution:
In $\triangle \mathrm{AFE}$, we get $\mathrm{AF}=\mathrm{AE}$
$\therefore \triangle \mathrm{AFE}$ is an isosceles $\Delta$
$\operatorname{ar}(\triangle \mathrm{ABC})=\operatorname{ar}(\triangle \mathrm{ABD})+\operatorname{ar}(\Delta \mathrm{ADC})$
$=\frac{1}{2} \mathrm{bc} \sin \mathrm{A}=\frac{1}{2} \mathrm{c} \mathrm{AD} \sin \frac{\mathrm{A}}{2}+\frac{1}{2} \mathrm{bAD} \sin \frac{\mathrm{A}}{2}$
$2 \mathrm{bcsin} \frac{\mathrm{A}}{2} \cos \frac{\mathrm{A}}{2}=\mathrm{AD} \sin \frac{\mathrm{A}}{2}(\mathrm{~b}+\mathrm{c})$
$\mathrm{AD}=\frac{2 \mathrm{bc} \cos \frac{\mathrm{A}}{2}}{\mathrm{~b}+\mathrm{c}}$
Also $\mathrm{AD}=\mathrm{AE} \cos \frac{\mathrm{A}}{2}$
$\mathrm{AE} \cos \frac{\mathrm{A}}{2}=\frac{2 \mathrm{bc} \cos \frac{\mathrm{A}}{2}}{\mathrm{~b}+\mathrm{c}}$
$\therefore \mathrm{AE}$ is $\mathrm{HM}$ of $\mathrm{b}$ and $\mathrm{c}$
Again $\mathrm{EF}=2 \mathrm{DE}=2 \mathrm{AD} \tan \frac{\mathrm{A}}{2}=\frac{2.2 \mathrm{bc} \cos \frac{\mathrm{A}}{2} \cdot \tan \frac{\mathrm{A}}{2}}{\mathrm{~b}+\mathrm{c}}$
$ =\frac{4 b c \sin \frac{A}{2}}{b+c} $
Hence option a, b, c, d are correct
4. In a triangle $\mathrm{ABC}$ with fixed base $\mathrm{BC}$, the vertex $\mathrm{A}$ moves such that $\cos \mathrm{B}+\cos \mathrm{C}=4 \sin ^{2} \frac{\mathrm{A}}{2}$
If $\mathrm{a}, \mathrm{b}$ and $\mathrm{c}$ denote the lengths of the sides of the triangle opposite to the angles $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ respectively, Then
(a). $\mathrm{b}+\mathrm{c}=4 \mathrm{a}$
(b). $\mathrm{b}+\mathrm{c}=2 \mathrm{a}$
(c). locus of point $\mathrm{A}$ is an ellipse
(d). locus of point $\mathrm{A}$ is a pair of straight lines.
Show Answer
Solution:
Given that $\cos B+\cos C=4 \sin ^{2} \frac{A}{2}\hspace{2cm}$ $\because \sin \frac{A}{2}=\sin \frac{\pi}{2}-\frac{B+C}{2}=\frac{\cos B+C}{2}$
$2 \cos \frac{\mathrm{B}+\mathrm{C}}{2} \cos \frac{\mathrm{B}-\mathrm{C}}{2}=4 \sin ^{2} \frac{\mathrm{A}}{2}$
$\frac{\cos \left(\frac{\mathrm{B}-\mathrm{C}}{2}\right)}{\cos \left(\frac{\mathrm{B}+\mathrm{C}}{2}\right)}=\frac{2}{1}$
Componendo and Dividendo
$\frac{\cos \frac{B-C}{2}+\cos \frac{B+C}{2}}{\cos \frac{B-C}{2}-\cos \frac{B+C}{2}}=\frac{2+1}{2-1}$
$\frac{2 \cos \frac{B}{2} \cos \frac{C}{2}}{2 \sin \frac{B}{2} \sin \frac{C}{2}}=3$
$\tan \frac{C}{2} \tan \frac{B}{2}=\frac{1}{3}$
$\frac{\mathrm{s}-\mathrm{a}}{\mathrm{s}}=\frac{1}{3}$
$3 \mathrm{~s}-3 \mathrm{a}=\mathrm{s}$
$2 \mathrm{~s}=3 \mathrm{a}$
$\mathrm{a}+\mathrm{b}+\mathrm{c}=3 \mathrm{a}$
$\mathrm{b}+\mathrm{c}=2 \mathrm{a} \Rightarrow \mathrm{AB}+\mathrm{AC}>\mathrm{BC}$
$\therefore$ locus of $A$ is an ellipse.
Hence options ‘b’ & ‘c’ are correct
Practice questions
1. The roots of the equation $6 x^{2}-5 x+1=0$ are $\tan \frac{A}{2}$ and $\tan \frac{B}{2}$ where $A, B, C$ are the angles of a triangle, then
(a). $\mathrm{a}^{2}+\mathrm{b}^{2}>\mathrm{c}^{2}$
(b). $\mathrm{a}^{2}+\mathrm{b}^{2}=\mathrm{c}^{2}$
(c). $\mathrm{a}^{2}-\mathrm{b}^{2}=\mathrm{c}^{2}$
(d). None of these
Show Answer
Answer: (b)2. If $\frac{\cos \mathrm{A}}{\mathrm{a}}=\frac{\cos \mathrm{B}}{\mathrm{b}}=\frac{\cos \mathrm{C}}{\mathrm{c}}$ and the side $\mathrm{a}=2$ then area of triangle is
(a). $1$
(b). $2$
(c). $\frac{\sqrt{3}}{2}$
(d). $\sqrt{3}$
Show Answer
Answer: (d)3. If in a triangle $\mathrm{PQR}, \sin \mathrm{P}, \sin \mathrm{Q}, \sin \mathrm{R}$ are in $\mathrm{A} . \mathrm{P}$ then
(a). The altitudes are in A.P
(b). The altitudes are in H.P
(c). The medians are in G.P
(d). The medians are in A.P
Show Answer
Answer: (b)4. If the sides $a, b, c$ of $\triangle A B C$ are in A.P then $\cot \frac{1}{2} \mathrm{~A}, \cot \frac{1}{2} \mathrm{~B}, \cot \frac{1}{2} \mathrm{C}$ are in
(a). A.P
(b). G.P
(c). H.P
(d). None of these
Show Answer
Answer: (a)5. If radius of the incircle of a triangle with sides $5 p, 6 p$ and $5 p$ is 6 , then $p$ is equal to
(a). 4
(b). 6
(c). 8
(d). 10
Show Answer
Answer: (a)6. In any $\triangle \mathrm{ABC}, \sum\left[\frac{\sin ^{2} \mathrm{~A}+\sin \mathrm{A}+1}{\sin \mathrm{A}}\right]$ is always greater than
(a). 9
(b). 3
(c). 27
(d). 10
Show Answer
Answer: (c)7. If $\mathrm{c}^{2}=\mathrm{a}^{2}+\mathrm{b}^{2}$, then $4 \mathrm{~s}(\mathrm{~s}-\mathrm{a})(\mathrm{s}-\mathrm{b})(\mathrm{s}-\mathrm{c})=$
(a). $\mathrm{s}^{4}$
(b). $b^{2} \mathrm{c}^{2}$
(c). $\mathrm{c}^{2} \mathrm{a}^{2}$
(d). $\mathrm{a}^{2} \mathrm{~b}^{2}$
Show Answer
Answer: (d)8. If $a, b, c, d$ be the sides of a quadrilateral, then the minimum value of $\frac{a^{2}+b^{2}+c^{2}}{d^{2}}$ is equal to
(a). $\frac{1}{2}$
(b). $\frac{1}{3}$
(c). $\frac{1}{4}$
(d). $1$
Show Answer
Answer: (b)9. $\frac{\mathrm{r} _{1}}{\mathrm{bc}}+\frac{\mathrm{r} _{2}}{\mathrm{ca}}=\frac{\mathrm{r} _{3}}{\mathrm{ab}}=$
(a). $\frac{1}{2 \mathrm{R}}-\frac{1}{\mathrm{r}}$
(b). $2 \mathrm{R}-\mathrm{r}$
(c). $\mathrm{r}-2 \mathrm{R}$
(d). $\frac{1}{\mathrm{r}}-\frac{1}{2 \mathrm{R}}$
Show Answer
Answer: (d)10. Passage
(a). $\frac{\mathrm{a}}{\sin \mathrm{A}}=2 \mathrm{R}, \mathrm{R}=\frac{\mathrm{abc}}{4 \Delta}$
(b). $\mathrm{r}=\frac{\Delta}{3}=(\mathrm{s}-\mathrm{a}) \tan \frac{\mathrm{A}}{2}=4 \mathrm{R} \sin \frac{\mathrm{A}}{2} \sin \frac{\mathrm{B}}{2} \sin \frac{\mathrm{C}}{2}$
(c). $\mathrm{r} _{1}=\frac{\Delta}{\mathrm{s}-\mathrm{a}}=\mathrm{s} \tan \frac{\mathrm{A}}{2}=4 \mathrm{R} \sin \frac{\mathrm{A}}{2} \cos \frac{\mathrm{B}}{2} \cos \frac{\mathrm{C}}{2}$
(d). If P be the orthocenter of a $\triangle \mathrm{ABC}$ and its distances PA from the vertex $\mathrm{A}$ and PL from the sides $\mathrm{BC}$ are $\mathrm{PA}=2 \mathrm{R} \cos \mathrm{A}, \mathrm{PL}=2 \mathrm{R} \cos \mathrm{B} \cos \mathrm{C}$
Answer the following questions based upon above passage
(i). If $r _{1}=2 r _{2}=3 r _{3}$, then
(a). $\frac{\mathrm{a}}{\mathrm{b}}=\frac{4}{5}$
(b). $\frac{\mathrm{a}}{\mathrm{b}}=\frac{5}{4}$
(c). $\frac{\mathrm{a}}{\mathrm{c}}=\frac{3}{5}$
(d). $\frac{\mathrm{a}}{\mathrm{c}}=\frac{5}{3}$
Show Answer
Answer: (b, d)(ii). $\frac{1}{\mathrm{r} _{1}^{2}}+\frac{1}{\mathrm{r} _{2}^{2}}+\frac{1}{\mathrm{r} _{3}^{2}}+\frac{1}{\mathrm{r}^{2}}=$
(a). $\frac{\mathrm{a}^{2}+\mathrm{b}^{2}+\mathrm{c}^{2}}{\mathrm{~s}^{2}}$
(b). $\frac{\sum \mathrm{a}^{2}}{\Delta^{2}}$
(c). $4 \mathrm{R}$
(d). $4 \mathrm{r}$
Show Answer
Answer: (b)(iii). $\frac{\mathrm{r} _{1}-\mathrm{r}}{\mathrm{a}}+\frac{\mathrm{r} _{2}-\mathrm{r}}{\mathrm{b}}=$
(a). $\frac{\mathrm{a}}{\mathrm{r} _{1}}$
(b). $\frac{\mathrm{b}}{\mathrm{r} _{2}}$
(c). $\frac{\mathrm{c}}{\mathrm{r} _{3}}$
(d). None of these
Show Answer
Answer: (c)(iv). In a triangle $\mathrm{ABC}$, let $\angle \mathrm{c}=\frac{\pi}{2}$. If $\mathrm{r}$ is the inradius and $\mathrm{R}$ is the circumradius of the triangle then $2(r+R)$ is equal to
(a). $a+b$
(b). $\mathrm{b}+\mathrm{c}$
(c). $\mathrm{c}+\mathrm{a}$
(d). $\mathrm{a}+\mathrm{b}+\mathrm{c}$





