Integral Calculus - Areas
The area bounded by the curve $\mathrm{y}=f(\mathrm{x})$, the $\mathrm{x}-$ axis, the ordinates $\mathrm{x}=\mathrm{a}$ & $\mathrm{x}=\mathrm{b}$ is $\mathrm{A}=\left|\int _{\mathrm{a}}^{\mathrm{b}} f(\mathrm{x}) \mathrm{dx}\right|$.
Curve sketching steps:
For sketching the graph of $f(\mathrm{x})$,
i. Determine domain, identifying where $f$ is not defined.
ii. Determine $\mathrm{x}$ intercept & y intercept, if possible.
iii. Determine asymptotes:
(a) For vertical asymptotes, check for rational function zero denominators, or undefined $\log$ function points.
(b) For horizontal asymptotes, consider $\lim \limits _{\mathrm{x} \rightarrow \pm \infty} f(\mathrm{x})$.
iv. Determine critical numbers,
(check where $f^{\prime}(\mathrm{x})=0$ or $f^{\prime}(\mathrm{x})$ does not exist, and finding intervals where $f$ is increasing or decreasing).
v. Determine inflection points.
(check where $f^{\prime \prime}(\mathrm{x})=0$ or $f^{\prime \prime}(\mathrm{x})$ or does not exist)
vi. plot intercepts, critical points, inflection points, asymptotes and other points as needed.
vii. Connect plotted points with smooth curve.
Some useful results
1. Area between $y^{2}=4 a x$ & $x^{2}=4$ by is $\dfrac{16 a b}{3}$ sq. units.
2. Area between $\mathrm{y}^{2}=4 \mathrm{ax}$ & its latus rectum is $\dfrac{8 \mathrm{a}^{2}}{3}$ sq.units.
3. Area between $\mathrm{y}^{2}=4 \mathrm{ax}$ & line $\mathrm{y}=\mathrm{mx}$ is $\dfrac{8 \mathrm{a}^{2}}{3 \mathrm{~m}^{3}}$ sq. units.
4. Area between $\sqrt{x}+\sqrt{y}=\sqrt{a}, x=0$ & $y=0$ is $\dfrac{a^{2}}{6}$ sq. units.
5. Area enclosed by $\left(\dfrac{\mathrm{x}}{\mathrm{a}}\right)^{2 / 3}+\left(\dfrac{\mathrm{y}}{\mathrm{b}}\right)^{2 / 3}=1$ is $\dfrac{3 \pi \mathrm{ab}}{8}$ sq. units.
6. Area of one $\operatorname{arc}$ of $\mathrm{y}=\operatorname{sinax}($ or $\mathrm{y}=\operatorname{cosax})$ and $\mathrm{x}$ axis is $2 / a$ sq. units.
7. Area of the region bounded by $y=|a x+b|($ or $x=|a y+b|)$ and $x$ axis (or $y$ axis) is $\dfrac{b^{2}}{a^{2}} s q$. units.
8. Area of $\dfrac{\mathrm{x}^{2}}{\mathrm{a}^{2}}+\dfrac{\mathrm{y}^{2}}{\mathrm{~b}^{2}}=1$ is $\pi$ab sq. units.
9. Area bounded by $\left\{(x, y): \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}} \leq 1 \leq \dfrac{x}{a}+\dfrac{y}{b}\right\}$ is $\dfrac{a b}{4}(\pi-2)$ sq.units.
10. Area of rhombus formed by $a x \pm b y \pm c=0$ is $\dfrac{2 c^{2}}{|a b|}$ sq. units.
11. Area of the triangle formed by $y=m _{1} x+c _{1}, y=m _{2} x+c _{2}, y=m _{3} x+c _{3}$ is $\dfrac{1}{2}\left|\sum \dfrac{\left(c _{1}-c _{2}\right)^{2}}{m _{1}-m _{2}}\right|$ sq. units.
Solved Examples:
1. The area of triangle formed by the tangent $&$ normal at the point $(1, \sqrt{3})$ on the circle $\mathrm{x}^{2}+\mathrm{y}^{2}=4$ and $\mathrm{x}-$ axis is
(a) 3
(b) $2 \sqrt{3}$
(c) $3 \sqrt{2}$
(d) 4
Show Answer
Solution:
Equation of tangent is $x+\sqrt{3 y}=4$.
Point $\mathrm{Q}$ is $(4,0)$
$\therefore$ Area of triangle $=\dfrac{1}{2} \cdot 4 \cdot \sqrt{3}=2 \sqrt{3}$ sq.units
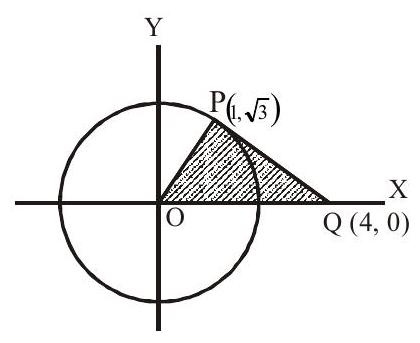
Answer: b
2. The area bounded by the curves $y=\sqrt{5-x^{2}}$ & $y=|x-1|$ is
(a) $\dfrac{5 \pi-1}{4}$
(b) $\dfrac{5 \pi+1}{4}$
(c) $\dfrac{5 \pi-2}{4}$
(d) $\dfrac{5 \pi-3}{4}$
Show Answer
Solution:
The two shaded areas are congruent
$\therefore$ Area $\mathrm{ACEF}=\dfrac{\text { Area of circle }}{4}-$ Area $\triangle \mathrm{OAD}$
$=\dfrac{5 \pi}{4}-\dfrac{1}{2}=\dfrac{5 \pi-2}{4}$ sq.units
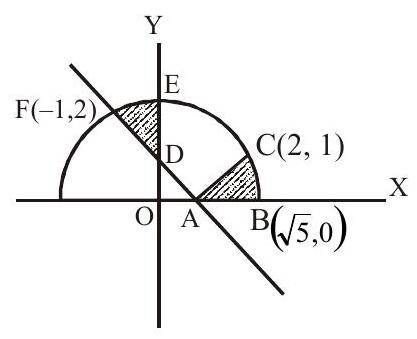
Answer: c
3. If two circles each of unit radius intersect orthogonally, the common area of the circle is
(a) $\dfrac{2 \pi}{3}-\sqrt{3}$
(b) $\dfrac{2 \pi}{3}+\sqrt{3}$
(c) $\dfrac{2 \pi}{3}-\dfrac{\sqrt{3}}{2}$
(d) $\dfrac{2 \pi}{3}+\dfrac{\sqrt{3}}{2}$
Show Answer
Solution:
Required area $=2$. Area of sector $\mathrm{ABC}-$ Area of square $\mathrm{ABCD}$
$=\left(\dfrac{90}{360} \cdot \pi\right) 2-1^{2}=\dfrac{\pi}{2}-1$ sq.units.
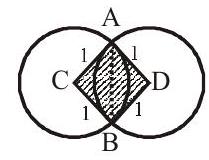
Answer: d
4. The possible values of $m$ for which the area bounded by the curves $y=x-x^{2}$ and $y=m x$ equal to $\dfrac{9}{2}$ sq. unit is
(a) -4
(b) -2
(c) 2
(d) none of these
Show Answer
Solution: The curves meet at $\mathrm{x}=0$ and $\mathrm{x}=1-\mathrm{m}$
$\begin{aligned} & \therefore \int _{0}^{1-m}\left(x-x^{2}\right)-m x \cdot d x= \pm \dfrac{9}{2} \\ \\ & \Rightarrow \int _{0}^{1-m}(1-m) x-x^{2} \cdot d x= \pm \dfrac{9}{2} \\ \\ & \Rightarrow \left((1-m) \dfrac{x^{2}}{2}-\dfrac{x^{3}}{2}\right) _{0}^{1-m}= \pm \dfrac{9}{2} \\ \\ & \Rightarrow (1-m)^{3}\left(\dfrac{1}{2}-\dfrac{1}{3}\right)=\dfrac{9}{2} \\ \\ & \Rightarrow (1-m)^{3}= \pm 27 \\ \\ & \Rightarrow 1-m= \pm 3 \\ \\ & \Rightarrow m=-2,4 \end{aligned}$
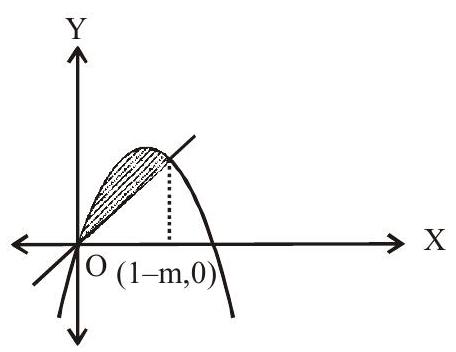
Answer: b
5. The area bounded by the curves $y=\log _{e} x, y=\log _{e}|x|, y=\left|\log _{e} x\right|$ and $y=\left|\log _{e}\right| x||$ is.
(a) 4
(b) 6
(c) 10
(d) 12
Show Answer
Solution:
$\therefore \mathrm{A}=4 \int _{0}^{1}\left|\log _{\mathrm{e}} \mathrm{x}\right| \mathrm{dx}=-4 \int _{0}^{1} \log _{\mathrm{e}} \mathrm{x} \mathrm{dx}$
$=-4\left(x \log _{\mathrm{e}} \mathrm{x}-\mathrm{x}\right) _{0}^{1}$
$=-4(-1-0)$
$=4$ sq.units.
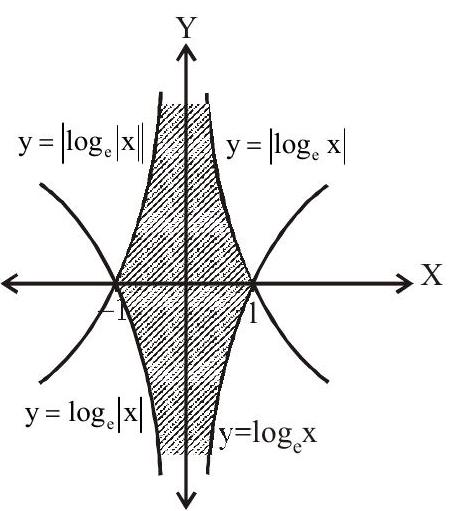
Answer: a
6. The ratio in which the area bounded by the curves $y^{2}=12 x$ & $x^{2}=12 y$ is divided by the line $\mathrm{x}=3$ is
(a) $15: 49$
(b) $13: 37$
(c) $15: 23$
(d) $17: 50$
Show Answer
Solution:
Required ratio $=\dfrac{\int _{0}^{3} \sqrt{12 x}-\dfrac{x^{2}}{12} \cdot d x}{\int _{0}^{3} \sqrt{12 x}-\dfrac{x^{2}}{12} \cdot d x}=\dfrac{15}{49}$
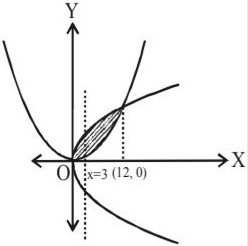
Answer: a
7. The area bounded by the curve $\mathrm{y}=\mathrm{x}+\sin \mathrm{x}$ and its inverse between the ordinates $\mathrm{x}=0$ and $\mathrm{x}=2 \pi$ is
(a) $4 \pi$
(b) $8 \pi$
(c) 4
(d) 8
Show Answer
Solution:
$A=2 \int _{0}^{2 \pi}(x+\sin x)-x d x=4 \int _{0}^{\pi}(x+\sin x)-x d x$
$=2.2(-\cos x) _{0}^{\pi}$
$=4(-\cos \pi+\cos 0)$
$=8$
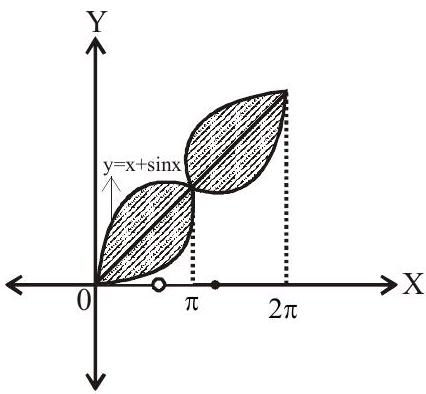
Answer: d
Exercise:
1. The area bounded by $\mathrm{y}=f(\mathrm{x})$, the $\mathrm{x}$-axis and the ordintes $\mathrm{x}=1$ & $\mathrm{x}=\mathrm{b}$ is $(\mathrm{b}-1) \sin (3 \mathrm{~b}+4)$. Then $f(\mathrm{x})$ is
(a) $(x-1) \cos (3 x+4)$
(b) $8 \sin (3 x+4)$
(c) $\sin (3 x+4)+3(x-1) \cos (3 x+4)$
(d) none of the above
Show Answer
Answer: c2. The triangle formed by the tangent to the curve $f(x)=x^{2}+b x-b$ at the point $(1,1)$ and the coordinate axes, lies in the first quadrant. If its area is 2 , then the value of $b$ is
(a) -1
(b) 3
(c) -3
(d) 1
Show Answer
Answer: c3. The area bounded by $y=(x-1)^{2}, y=(x+1)^{2}$ & $y=\dfrac{1}{4}$
(a) $\dfrac{1}{3}$ sq.unit
(b) $\dfrac{2}{3}$ sq.unit
(c) $\dfrac{1}{4}$ sq.unit
(d) $\dfrac{1}{5}$ sq.unit
Show Answer
Answer: a4. Let the straight line $\mathrm{x}=\mathrm{b}$ divide the area enclosed by $\mathrm{y}=(1-\mathrm{x})^{2}, \mathrm{y}=0$ & $\mathrm{x}=0$ into two parts $R _{1}(0 \leq x \leq b)$ & $R _{2}(b \leq x \leq 1)$ such that $R _{1}-R _{2}=\dfrac{1}{4}$. Then $b$ is
(a) $\dfrac{3}{4}$
(b) $\dfrac{1}{2}$
(c) $\dfrac{1}{3}$
(d) $\dfrac{1}{4}$
Show Answer
Answer: b5. The area of the quadrilateral formed by the tangents at the end points of latus rectum to the ellipse $\dfrac{x^{2}}{9}+\dfrac{y^{2}}{5}=1$ is
(a) $\dfrac{27}{4}$ sq.unit
(b) 9 sq.unit
(c) $\dfrac{27}{2}$ sq.unit
(d) 27 sq.unit
Show Answer
Answer: d6. The area of the region containing the points ( $x, y$ ) satisfying $4 \leq x^{2}+y^{2} \leq 2(|x|+|y|)$ is
(a) 8 sq.units
(b) 2 sq.units
(c) $4 \pi$ sq.units
(d) $2 \pi$ sq.units
Show Answer
Answer: a7. The area of the region between the curves $y=\sqrt{\dfrac{1+\sin x}{\cos x}}$ and $y=\sqrt{\dfrac{1-\sin x}{\cos x}}$ bounded by the lines $\mathrm{x}=0$ & $\mathrm{x}=\dfrac{\pi}{4}$ is
(a) $\int _{0}^{\sqrt{2}-1} \dfrac{\mathrm{tdt}}{\left(1+\mathrm{t}^{2}\right) \sqrt{1-\mathrm{t}^{2}}}$
(b) $\int _{0}^{\sqrt{2}-1} \dfrac{4 \mathrm{t}}{\left(1+\mathrm{t}^{2}\right) \sqrt{1-\mathrm{t}^{2}}} \mathrm{dt}$
(c) $\int _{0}^{\sqrt{2}+1} \dfrac{4 \mathrm{t}}{\left(1+\mathrm{t}^{2}\right) \sqrt{1-\mathrm{t}^{2}}} \mathrm{dt}$
(d) $\int _{0}^{\sqrt{2}+1} \dfrac{\mathrm{t}}{\left(1+\mathrm{t}^{2}\right) \sqrt{1-\mathrm{t}^{2}}} \mathrm{dt}$
Show Answer
Answer: b8. Read the passage and answer the following questions:-
If the curve $y=f(x)$ satisfy the equation $y\left(x+y^{3}\right) d x=x\left(y^{3}-x\right) d y$ and $g(x)$
$g(x)=\int _{1 / 8}^{\sin ^{2} x} \sin ^{-1} \sqrt{t} d t+\int _{1 / 8}^{\cos ^{2} x} \cos ^{-1} \sqrt{t} d t$, where $x \in\left[0, \dfrac{\pi}{2}\right]$, then
i. Equation of curve $\mathrm{y}=f(\mathrm{x})$ passes through $(4,-2)$ is
(a) $3 y=(-54 x)^{\dfrac{1}{3}}$
(b) $2 y=(-16 x)^{\dfrac{1}{3}}$
(c) $y=(-2 x)^{\dfrac{1}{3}}$
(d) none of these
ii. Area bounded by curve $\mathrm{y}=f(\mathrm{x}), \mathrm{g}(\mathrm{x})$ and $\mathrm{y}$ axis is
(a) $\dfrac{1}{4}\left(\dfrac{3 \pi}{16}\right)^{4}$
(b) $\dfrac{1}{8}\left(\dfrac{3 \pi}{16}\right)^{4}$
(c) $\dfrac{1}{8}\left(\dfrac{3 \pi}{8}\right)^{4}$
(d) none of these
Show Answer
Answer: (i) c (ii) b9. The maximum area of the rectangle whose sides pass through the angular points of a given rectangle of sides $a \& b$ is
(a) $\dfrac{1}{2}(\mathrm{ab})^{2}$
(b) $\dfrac{1}{2}(a+b)$
(c) $\dfrac{1}{2}(a+b)^{2}$
(d) none of these
Show Answer
Answer: c10. Consider a square with vertices at $(1,1),(-1,1),(-1,-1)$ & $(1,-1)$. Let $S$ be the region consisting of all points inside the square which are nearer to the orgin than to any edge. Area of the region is________________________
Show Answer
Answer: $\dfrac{4}{3}(4 \sqrt{2}-5)$11. The area bounded by $\min (|x|,|y|)=2$ and $\max (|x|,|y|)=4$ is
(a) 8 sq.unit
(b) 16 sq.unit
(c) 24 sq.unit
(d) 32 sq.unit
Show Answer
Answer: b12. The area of the region bounded by
$[x]^{2}=[y]^{2} \text {, if } x \in[1,5] \text { is }$
(a) 4
(b) 8
(c) 5
(d) 10
Show Answer
Answer: b13. Match the following:-
| Column I | Column II | ||
|---|---|---|---|
| a. | Area enclosed by $[\mathrm{x}]^{2}=[\mathrm{y}]^{2} \text { for } 1 \leq \mathrm{x} \leq 4$ | (p) | 8 sq.units |
| b. | Area enclosed by $[|x|]+[|y|]=2$ | (q) | 6 sq.units |
| c. | Area enclosed by $[|x|][|y|]=2$ | (r) | 4 sq.units |
| d. | Area enclosed by $\dfrac{| \mathrm{x} \mid]}{| \mathrm{y} \mid]}=2,-5 \leq \mathrm{x} \leq 5$ | (s) | 12 sq.units |





