Current Electricity Ques 100
- In the experimental set up of meter bridge shown in the figure, the null point is obtained at a distance of $404 $ $ cm$ from $A$. If a $10$ $ \Omega$ resistor is connected in series with $R _1$, the null point shifts by $10 $ $cm$. The resistance that should be connected in parallel with $\left(R _1+10\right) \Omega$ such that the null point shifts back to its initial position is
(Main 2019, 11 Jan II)
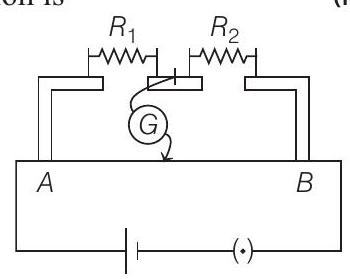
(a) $60 $ $\Omega$
(b) $20 $ $\Omega$
(c) $30 $ $\Omega$
(d) $40 $ $\Omega$
Show Answer
Answer:
Correct Answer: 100.(a)
Solution:
Formula:
- For meter bridge, if balancing length is $l cm$, then in first case, $\frac{R _1}{R _2}=\frac{l}{(100-l)}$
It is given that, $l=40 cm$,
$ \begin{aligned} \text { So, } & \quad \frac{R _1}{40} =\frac{R _2}{100-40} \\ \text { or } & \quad \frac{R _1}{R _2} =\frac{2}{3} \quad …….(i) \end{aligned} $
In second case, $R _1^{\prime}=R _1+10$, and balancing length is now $50 cm$ then
or
$\frac{R _1+10}{50}=\frac{R _2}{(100-50)} $
$R _1+10=R _2 \quad …….(ii) $
Substituting value of $R _2$ from (ii) to (i) we get,
$ \begin{aligned} \text { or } & \quad \frac{R _1}{10+R _1} =\frac{2}{3} \\ \Rightarrow & \quad 3 R _1 =20+2 R _1 \\ \text { or } & \quad R _1 =20 \Omega \\ \Rightarrow & \quad R _2 =30 \Omega \end{aligned} $
Let us assume the parallel connected resistance is $x$.
Then equivalent resistance is $\frac{x\left(R _1+10\right)}{x+R _1+100}$
So, this combination should be again equal to $R _1$.
$\frac{\left(R _1+10\right) x}{R _1+10+x} =R _1 $
$\Rightarrow \quad \frac{30 x}{30+x} =20 $
$\text { or } \quad 30 x =600+20 x $
$\text { or } \quad x =60 $ $\Omega$





