Current Electricity Ques 113
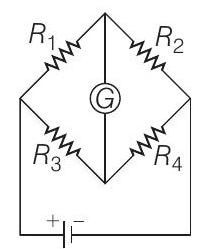
- The Wheatstone bridge shown in figure here, gets balanced when the carbon resistor is used as $R _1$ has the color code (orange, red, brown). The resistors $R _2$ and $R _4$ are $80$ $ \Omega$ and $40$ $\Omega$, respectively.
Assuming that the color code for the carbon resistors gives their accurate values, the color code for the carbon resistor is used as $R _3$ would be
(2019 Main, 10 Jan II)
(a) brown, blue, black
(b) brown, blue, brown
(c) grey, black, brown
(d) red, green, brown
Show Answer
Answer:
Correct Answer: 113.(b)
Solution:
Formula:
- The value of $R _1$ (orange, red, brown)
$ \Rightarrow \quad 32 \times 10=320$ $ \Omega $
Given, $R _2=80$ $ \Omega$ and $R _4=40 $ $\Omega$
In balanced Wheatstone bridge condition,
$\frac{R _1}{R _2}=\frac{R _3}{R _4} \Rightarrow \quad R _3=R _4 \times \frac{R _1}{R _2} $
$\Rightarrow \quad R _3=\frac{40 \times 320}{80} $
$\text { or } \quad R _3=160 \Omega=16 \times 10^{1}$
Comparing the value of $R _3$ with the colours assigned for the carbon resistor, we get
$R _3=16 \times 10^{1} $
$\quad\quad \nearrow \uparrow \quad\quad\uparrow$
${\text {Brown Blue Brown }}$





